博客

该博客是根据百度贴吧利_刃网友的内容进行整理的，原出处

请点击此处

！

2.1 统计学(Statistic)

统计学是通过搜索、整理、分析数据等手段，以达到推断所测对象的本质，甚至预测对象未来的一门综合性科学。其中用到了大量的数学及其它学科的专业知识，它的使用范围几乎覆盖了社会科学和自然科学的各个领域。

2.2 概率论(Probability Theory)

概率论是研究随机性或不确定性等现象的数学分支，用来模拟实验在同一环境下会产生不同结果的情况。典型的随机实验有掷骰子、扔硬币、抽扑克牌以及轮盘游戏等。概率论的主题是研究随机变量和随机变量的概率分布。

概率论和统计学的关系：


概率论是统计学的基石。从科学史的角度看，它们一开始完全是独立发展的。统计学的发展经历了计数→统计→统计学的阶段。而概率论却是在数学家解答赌博中出现的大量问题后产生的。18世纪中后期，统计学由于吸收了概率论的观念与方法，才使统计的水平真正上升到了科学、成熟和完善的程度，而概率论，由于和统计学的结合，走出了纯数学的圈子，获得了广泛的应用。

2.3 函数(Function)

定义：有两个变量x、y，如果对于x在某一范围内的每一个确定的值，y都有唯一确定的值与它对应，那么就称y是x的函数。其中x是输入值，y是输出值。可以表示为：输入值x→函数(对应关系规则)→输出值y，即：f:X→Y。

按中文版的定义，会理解为函数就是变量y。而英文版函数指的是x和y之间的对应关系(A function is a relation between a set of inputs and a set of permissible outputs…)。记作：f(x) 中文读作：f(x)英文读作：f of x。

例1：有两组数字，X={1,2,3,4}，Y={3,5,7,9}，对于X中的每一个数字，Y中都有一个数字和它产生一对一的对应关系，这个对应关系就是“乘2加1”，也就是说，Y中的每个数字是X的数字乘2加1之后得到的，因此X与Y具有函数关系。

例2：下图是以颜色作为函数对应关系的。

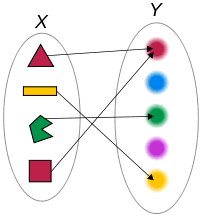
函数可以用两个变量(x, y)来描述，符号表示为y=f(x)，代表x和y之间存在某种数学运算关系，x经过某种运算之后可以得到y的值。例如y=x+1, y=x/2+3, y=x^2等。

y=x+1也可以记作f(x)=x+1，这是一种单变量表示法。为了表示特定的函数，f和x都可以用其它字母或单词来代替，例如P(A), sin(x), h(θ)等。

函数图形可以用2D曲线来表示，图中横轴代表x，纵轴代表f(x)。例如f(x)=x^2，图形为二次曲线：

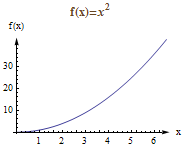
前面介绍的函数只有一个输入值，如果有多个输入值，就称为多元函数。f(x,y)可以表示一个二元函数，二元函数可以用3D曲面来表示。例如f(x,y)=x^2+y^2，图形表示如下：

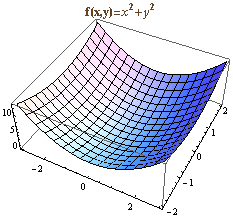
二元以上的函数很难用图形来表示，只能分解成2D或3D图形来逐层显示，因此研究多元函数一般都以二元函数为代表。

注意：编程中的函数概念和数学中的函数概念并不相同，编程函数除了可以表示数学函数的意义之外，还可以代表命令、过程、(类的)方法、事件、语句成组、封装等含义，输入参数可以是0个或多个，返回值(输出值)可有可无。

Function(函数)这个数学名词是莱布尼兹在1694年开始使用的，中文的“函数”一词由清朝数学家李善兰译出。

2.4 随机变量(Random Variable)

随机变量是概率论的基础概念，对随机变量的研究是概率论的核心内容。

日常生活中，由于不同条件下偶然因素的影响，会产生许多随机的、无法预先确定的数值，随机变量就是指这些随机出现的非确定值。例如某一时刻某停车场的车辆数量，某地区的粮食年产量，某人20岁时的身高、体重等，都是随机变量的实例。

定义：随机变量X是定义在样本空间Ω上的输出值为实数的函数，对于样本空间Ω上的每一个样本点e，都有一个数值X(e)与之对应。X可代表Ω中的每一个样本点。

记作：X 或 Y,Z (大写字母X,Y,Z表示随机变量，小写字母x,y,z表示随机变量的取值)

注意：由定义可以看出，随机变量实质上是一个函数。通过二元函数可以很容易看出这一点，例如同时掷两枚骰子，可以产生两个随机数i和j，而随机变量X可以是i,j之和，用函数表示为X(i,j)=i+j。

随机函数一词并不是指随机变量，而是指编程时为生成随机数而编写的命令，例如C、Matlab的rand()或Java的Math.random()等。计算机生成的随机数是伪随机数，是可以预测的，不过在实际应用中一般没什么大碍。

按随机变量的取值，可分为

离散型

和

连续型

两种类型：

离散型(Discrete)：

随机变量取值为有限个，数值可以一一列举出来，例如x为5、6、7这三个数之一。掷一枚骰子，其结果必然是1~6这六个数之一，不可能出现1.5或3.618之类的数字，因此是离散型。某地区某年人口的出生数、死亡数，某药治疗某病病人的有效数、无效数等都是离散型。离散型的图形可以用散点图来表示：

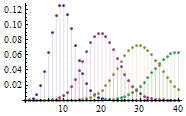
连续型(Continuous)：

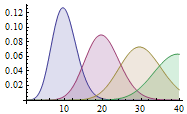
随机数X的取值有无限种可能，例如x为0～1范围之间的任意一个数：0.01、0.512、0.999…。再例如某地区6岁儿童的身高、体重值，某种食物的酸碱度ph值等都是连续型。连续型的图形可以用连续的曲线来表示：

%%%%%% Matlab代码: %%%%%%
rand(1) % 产生一个随机数(连续)
% ans = 0.6324 也可能是0~1之间的其它任意值

10 + (50-10) * rand(1) % 产生一个10~50之间的随机数(连续)
% ans = 47.3597

rand(1, 3) % 产生1行3列随机数(连续)
% ans = 0.9649 0.1576 0.9706

randint(1, 2, [0,3]) % 产生1行2列随机数(离散)，范围0~3，即{0,1,2,3}中的一个
% ans = 2 0

2.5 总和(Sum)

也称总计、合计、累计、连加，求一组数字连加所得的总和。运算符：∑ 读法：希腊字母读音sigma(西格玛)，一般读作sum(萨姆)。公式：

$$\sum_{i=1}^nx_i=x_1+x_2+...+x_n$$
∑符上面的n和下面的i=1代表从第1个数字一直加到第n个，xi代表一组数字的每一个。

例1：求1+1等于几？

(惊讶，1+1居然也有这么高深的写法)

$$\sum_{i=1}^21=1+1=2$$

例2：求1、2、3、4这四个数字相加的总和。

$$\sum_{i=1}^nx_i=1+2+3+4=10 \ \ (x=[1,2,3,4])$$

%%%%%% Matlab代码: %%%%%%
sum([1 2 3 4])
% ans = 10

2.6 连乘积(Product)

求一组数字连乘所得的乘积。运算符：








∏










$\prod$
读法：








∏










$\prod$
是圆周率π(派)的大写，读作prod(普若德)或product。前面讲过的链式法则和一些概率连乘公式都能以








∏










$\prod$
运算符的形式来表示。公式：

$$\prod_{i=1}^nx_i=x_1 \times x_2 \times x_3...x_n$$
例：求1、2、3、4这四个数字相乘所得的结果。

$$\prod_{i=1}^nx_i=1 \times2 \times3 \times4=24 \ \ (x=[1,2,3,4])$$

%%%%%% Matlab代码: %%%%%%
prod([1 2 3 4])
% ans = 24

【阶乘(Factorial)】

是指1×2×3×4……一直乘到所要求的数。运算符：! ，公式：

$$\prod_{i=1}^ni=1 \times2 \times....\times n$$

例：

3！= 1×2×3 = 6

5！= 1×2×3×4×5 = 120

注意：小数不能作阶乘，不过Gamma函数可以定义为小数版的阶乘。

%%%%%% Matlab代码: %%%%%%
factorial(5) % 5!
% ans = 120

vpa(*5!*) % 同factorial(5)
% ans = 120

2.7 乘积(Multiply)

也称元素乘积(Element-By-Element Multiplication)，是指两组数字一一对应相乘。运算符：×、.* 或 *

公式：

$$A\times B=\{ a_1,a_2,....,a_n\} \cdot \{ b_1,b_2,....,b_n\} =\{ a_1 \times b_1,a_2 \times b_2,....,a_n \times b_n\}$$

注意：乘积要求两组数字的数量相等，后面要讲的差值、加权求和等也是这样。

%%%%%% Matlab代码: %%%%%%
A = [9, 2, 8, 2]; B = [1, 2, 3, 4];
A .* B
% ans = 9 4 24 8

两张图片乘积时的效果，就是Photoshop中的正片叠底(Multiply)效果。颜色值范围0~1，白色为1，因此白色部分会保持另一张图的原色不变，其它颜色会相应变暗。

%%%%%% Matlab(上图的实现代码): %%%%%%
% 要求两张图片同样大小
% imread是读取某张图片
% im2single表示R、G、B颜色分开处理
img1 = im2single(imread('c:/a1.jpg'));
img2 = im2single(imread('c:/a2.jpg'));
imgDot = img1 .* img2; % 两张图片点乘
imshow(imgDot); % 显示图片

[注] 受Matlab的影响，中文教程有时也称元素乘积为点乘。Matlab的元素乘积命令为times(a,b)，运算符为.

；矩阵乘法命令为mtimes(a,b)，运算符为

。

2.7 点乘(Dot Product)

也称点积、内积(Inner Product)、纯量积(Scalar Product)、数量积、标量积、标积、加权求和，是指两组数字一一对应相乘，再求全部乘积的总和。运算符：

\bullet







∙










$\bullet$
或记作

<\vec a, \vec b>







<







a








⃗













,







b








⃗













>










<script type=”math/tex” id=”MathJax-Element-12″><\vec a, \vec b></script>。

公式1：


A\cdot B=\sum_{i=1}^na_i,b_i= a_1 \times b_1+a_2 \times b_2+….+a_n \times b_n

$$A\cdot B=\sum_{i=1}^na_i,b_i= a_1 \times b_1+a_2 \times b_2+....+a_n \times b_n$$

注意：从公式来看，点积其实就是加权求和，因为应用领域不同所以有不同的名称。

%%%%%% Matlab代码: %%%%%%
A = [3, 4, 2]; B = [6, 3, 1];
dot(A, B)
% ans = 32

向量的点积


是求两个向量(两条线段)夹角的重要工具。应用很广，除了数据向量分析之外，图像旋转、鼠标交互旋转图形、3d光照、反射折射、碰撞检测等都离不开它。有关向量的几何意义，将在后面的章节详细讨论。

公式2：


A \cdot B =|A||B|cos\theta

$$A \cdot B =|A||B|cos\theta$$

公式2为两个向量的夹角公式|A|为向量a的模，即向量A的长度|A|*cosθ是A到B的投影，当点积A·B=0时，cosθ=0，因此角θ=90度，说明两个向量正交(两条线段垂直)。

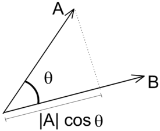
设：向量a=OA, 向量b=OB, 角θ=∠AOB

两向量夹角公式为：a·b = |a|

|b|

cosθ

因此，θ角度 = acos(a·b/|a|/|b|)

a·b就是向量a、b的点积，a·b = ax*bx + ay*by

|a|为向量a的模，即向量a的长度，|a| = sqrt(ax^2+ay^2)

判断角θ的正负值：当(x1*y2 – y1*x2 > 0)时，角θ为正值，顺时针旋转；当(x1*y2 – y1*x2 < 0)时，角θ为负值，逆时针旋转。

矩阵的点积

–

点积是矩阵乘法的一个步骤，广泛应用于人工智能的图像识别、人工神经网络、自然语言处理等各个领域。有的软件直接使用点积运算符(·)作为矩阵乘法的运算符，例如Mathematica。

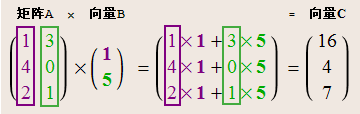
公式3：


A \cdot B =A \times B^T

$$A \cdot B =A \times B^T$$
B^T或B*代表矩阵转置，转置后可以使用矩阵乘法来计算点积。

%%%%%% Matlab代码: %%%%%%
A = [3, 4, 2]; B = [6, 3, 1];
A * B*
% ans = 32

2.8 平均值(Mean, Average)

也称均值、平均数或期望值，一般是指一组数字的算术平均值，是n个数字相加的总和再除以n。此外还有几何平均值、平方平均值、加权平均值等。记作：

\bar X, \mu 或 E(X)












X








¯









,


μ





或





E




(


X




)










$\bar X, \mu 或 E(X)$
， 读法：x顶上加条横线，读x-bar(X拨)；μ读作mu(缪,木有) ,公式：


\bar X= \frac{1}{n}\sum_{i=1}^nx_i=\frac{x_1+x_2+….+x_n}{n}

$$\bar X= \frac{1}{n}\sum_{i=1}^nx_i=\frac{x_1+x_2+....+x_n}{n}$$
读作：平均值 = 总和 / 数量

[注] 统计学教材建议用

\bar X












X








¯

















$\bar X$
代表样本平均值，用

\mu







μ










$\mu$
代表总体平均值。

图像的分块平均和全部平均。

求三张图片的平均值，相当于每张图片以1/3的透明度叠加起来。

%%%%%% Matlab(上图的实现代码): %%%%%%
% 要求3张图片同样大小
img1 = im2single(imread('a1.jpg'));
img2 = im2single(imread('a2.jpg'));
img3 = im2single(imread('a3.jpg'));
imgMean = (img1+img2+img3) / 3; % 求平均值
imshow(imgMean); % 显示图片

人脸识别中的“平均脸”就是以此方法求出。

2.9 加权求和(Weighted Sum)

也称线性加权法、线性加权和，是指两组数字一一对应相乘(点乘)，再求全部乘积的总和。“权”的本意是秤砣，这里是权重(Weight)的意思，是指调节数值平衡所加入的缩放比例值，有时也称系数(Coefficient)。记作：








Σ


X




⋅


W




,


⊕










$\Sigma X \cdot W, \oplus$
，公式：

$$X \oplus W=\sum_{i=1}^n x_i w_i=x_1w_1+x_2w_2+...+x_nw_n$$
例1：求下列数字的总和：3、4、3、3、3、2、4、4、3、3

一般求法为：3+4+3+3+3+2+4+4+3+3 = 32，观察一下这组数字，发现其中3出现6次，4出现3次，2出现1次。共出现了三种数字，表示为：X={3,4,2}；次数单独列出来：W={6,3,1}，这组次数W称为“权重”。因此，

$$∑X·W = ∑{3,4,2}*{6,3,1} = 3*6 + 4*3 + 2*1 = 18 + 12 + 2 = 32$$

加权求和法是决策论中多目标决策分析(MCDA)的一种最基本的方法。

例2：假设游戏角色的攻击力、防御力、血量的重要度比例分别是5: 2: 3，这时如果两个角色的属性值分别是：吸血鬼={攻300, 防500, 血1200}和狼人={攻700, 防600, 血800}，比较一下谁厉害。

吸血鬼 = 300*5 + 500*2 + 1200*3 = 6100

狼人 = 700*5 + 600*2 + 800*3 = 7100

看来还是狼人厉害。

例3：Sam要买一款性价比最好的相机，假设相机的性格比为 图像质量:电池电量:价格=0.6:0.1:-0.3(价格越小越好)，现在两款相机分别是：Sony={图像8000,电量230,价格980}、Canon={图像12000,电量120,价格1300}，到底买哪一款好呢？

Sony = 8000*0.6 + 230*0.1- 980*0.3 = 4529

Canon = 12000*0.6 + 230*0.1-1300*0.3 = 6833

显然是买Canon更划算。

加权求和是矩阵乘法的一个步骤，广泛应用于人工智能的图像识别、人工神经网络、自然语言处理等各个领域。

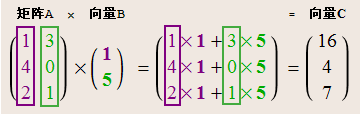
%%%%%% Matlab代码: %%%%%%
A = [3, 4, 2]; B = [6, 3, 1];
wsum = sum(A .* B)
% wsum = 32

2.10 期望值(Expectation)

也称数学期望、平均值，是随机变量的加权平均值(Weighted Average)。可以理解为试验中每次可能结果的概率乘以其结果的总和(公式1)；还可以理解为样本空间中每种样本的属性值和数量的加权求和，再除以样本总数(公式2)。记作：E[X]、













X








¯

















$\bar X$
、μ 或 支 (“支”是纵向的“+|×”)

公式1：

$$E[X]=\sum_{i=1}^nx_ip_i,(for \sum_{i=1}^np_i=1)$$
xi代表每次试验结果，pi代表xi的概率，样本空间的总概率为1

公式2：

$$E[X]=\frac{\sum_{i=1}^nx_iw_i}{\sum_{i=1}^nw_i}$$

简记法：

$$E[X]=\frac{X \oplus W }{\sum W}$$

读作：加权平均值 = 加权求和 / 权重的总和

注意：期望值并不是我们常识中的“期望”，而是指“平均值”。为什么称为期望呢？这是因为概率论的最初研究工作与赌博密切相关，其目的是研究平均情况下一个赌徒在赌桌上可以期望自己赢得多少钱。

例1：以掷骰子为例，我们知道，每掷一次每种点数的概率是1/6，那么平均每次会出现几个点呢？

从样本空间来看，平均值E[X] = 6个样本的总点数/样本总数 = (1+2+3+4+5+6)/6 = 21/6 = 3.5

例2：一件衣服卖出的价格有3种可能，卖5元的概率为1/6，10元为2/6，15元为3/6，求期望值。

公式1：E[X] = 5×1/6 + 10×2/6 + 15×3/6 = 70/6 ，(权重 1/6 + 2/6 + 3/6 = 1)

例3：一共6件衣服，其中有1件卖了5元，有2件卖了10元，剩下3件卖了15元，求平均每件卖多少钱(期望值)？

6件衣服的价格分别是：5, 10, 10, 15, 15, 15

公式2：E[X] = (5×1 + 10×2 + 15×3) / (1+2+3) = 70/6

加权平均值和算术平均值的差别：


◇加权平均值：0.3*A+0.7*B (权重0.3+0.7=1)

◇算术平均值：(A+B)/2 = 0.5*A + 0.5*B (权重都是0.5，可见算术平均值是一种权重相等的加权平均值)

2.11 中位数(Median)

也称中值、中间值，是指一组数字按大小顺序排列起来，处于中间位置的那个数字。如果数量为偶数，则中位数取于中间位置的两个数字的平均值(或者取两个数字的前面一个)。与中位数相似的概念还有：四分位数(Quartitles)、十分位数(Decile)、百分位数(Percentile)等。记作：m或 Me

例1：求 9, 12, 7, 16, 13 的中位数。

解：从小到大排序为 7, 9, 12, 13, 16，中位数取中间的数字12。

例2：求 3, 2, 4, 1 的中位数。

解：从小到大排序为 1, 2, 3, 4，中位数取2,3的平均数，即(2+3)/2=2.5。

%%%%%% Matlab代码: %%%%%%
median([9, 12, 7, 16, 13])
% ans = 12
median([3, 2, 4, 1])
% ans = 2.5000

中位数的一个典型应用是中值滤波(Median Filter)，是对图片进行边缘检测之前常用的预处理步骤，用来去除噪声，保护边缘特征。中值滤波的基本原理是把图像中每个像素点的灰度值用该点周围各点灰度值的中位数来代替，让每个像素接近周围像素的真实值，从而消除孤立的噪声点。

下图是中值滤波的效果演示，可以看出滤波后图像虽然变模糊了，但线条边缘部分还保持了一定的清晰度。

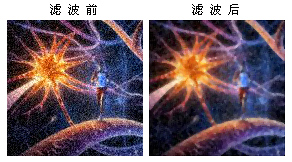
%%%%%% Matlab(上图的实现代码): %%%%%%
img1 = imread('c:/a1.jpg');
% 中值滤波只处理灰度图，因此彩色RGB图像要分离通道再处理
r = medfilt2(img1(:,:,1)); % 红
g = medfilt2(img1(:,:,2)); % 绿
b = medfilt2(img1(:,:,3)); % 蓝
img1(:,:,1) = r;
img1(:,:,2) = g;
img1(:,:,3) = b;
imshow(img1)

2.12 众数(Mode)

指一组数据中出现次数最多的那个数，众数可以是0个或多个。众数是直方图的最大值，也代表概率密度的峰值。记作：Mo

例1：1, 2, 3, 3, 4的众数是3。

例2：1, 2, 2, 3, 3, 4的众数是2和3。

例3：1, 2, 3, 4, 5没有众数。

众数可以用于非数字的集合，例如：{苹果，苹果，香蕉，橙，橙，橙，桃}的众数是“橙”。

%%%%%% Matlab代码: %%%%%%
% Matlab的众数是只取第一个
mode([1, 2, 3, 3, 4]) % ans = 3
mode([1, 2, 2, 3, 3, 4]) % ans = 2
mode([1, 2, 3, 4, 5]) % ans = 1

平均数、中位数、众数都可以代表一组数据的整体特征，而它们所代表的特征却是各有特色的。

2.13 阈值(Threshold)

也称临界值、二值化、阀值(文盲版)。阈，音yù，门限、边界、界限的意思。在一组数字中，按某个数值t的大小划一条分界线，分界线以上的为1，以下的为0，分界线的数值t就是阈值。阈值法是一种最简单的分类法。记作：t，公式：

$$f(n) = \begin{cases} out=1, & \text{if $in>t$ } \\ out=0, & \text{if $int \le t$ } \end{cases}$$

例：X = {0.1, 0.75, 0.32, 0.2}，t=0.2，因为{0.1<0.2, 0.75>0.2, 0.32>0.2, 0.2=0.2}，所以阈值处理之后的结果为{0, 1, 1, 0}。

阈值t的取值可以是0~1范围的任意数，默认值t=0.5。下图动画显示出阈值t=0.1~0.6的变化过程。

在手写或印刷文字的识别中，有必要对扫描的图像进行二值化的预处理。

%%%%%% Matlab(上图的实现代码): %%%%%%
img1 = imread('c:/a1.jpg');
lv = graythresh(img1); % 自动计算阈值t
imgT = im2bw(img1, lv);
imshow(imgT)

figure;
imgT = im2bw(img1, 0.3) % 设置阈值t=0.3
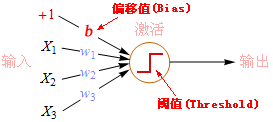
imshow(imgT)

阈值在人工神经网络中有重要的应用，最早的神经网络就是基于阈值逻辑(Threshold Logic)。感知器的hardlim是阈值函数，hardlim的阈值t=0。

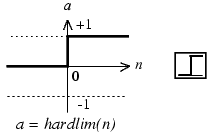
有大量的中文教程把神经网络的偏移值(Bias)也称为阈值，这是错误的，英文的相关文章几乎没有把Threshold和Bias混用的。

2.13 差值(Difference)

是指两组数字一一对应相减之后的值。记作：A-B 或 diff(A,B),公式：

$$A- B=\{ a_1,a_2,....,a_n\}- \{ b_1,b_2,....,b_n\} =\{ a_1 -b_1,a_2 - b_2,....,a_n - b_n\}$$

有两组数字分别为Sin和Sinc，图示它们的差值：

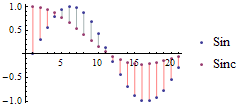
%%%%%% Matlab代码: %%%%%%
A = [9, 2, 8, 2]; B = [1, 2, 3, 4];
A - B
% A,B的差值为[8, 0, 5, -2]

% 注意：Matlab的diff命令是“逐次差分”，不是差值，而是一组数字中每两个相邻数字反向相减
C = [1, 2, 4, 7, 11];
diff(C)
% diff(C) = [2-1, 4-2, 7-4, 11-7] = [1, 2, 3, 4]

实际应用中，我们往往只关心两组数字之间的差距，不关心正负关系，因此要对差值取绝对值来处理，记作：|A-B|。差值常用来比较两组数据或两幅图之间的差异，相同的部分相减之后变为0，在图像上呈黑色。下图右侧图片的大面积黑色代表前两张图片相同的部分，而灰白色代表不同的地方，可见差值法是种找别扭的绝佳方式。

监控录像自动分析也常用到差值法，差值之后再做阈值处理。

2.14 离差(Deviate)

也叫离均差、差量、绝对差值，是指对于一组数字，每个数字分别减去平均值所得的值(或绝对值)。离差的总和为0。公式：

$$Dev(X)=x-\bar x$$

有一组数字X，图示它的离差：(蓝竖线的总长度=红竖线的总长度)

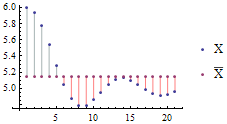
有一组数字X={2.9, 2.6, 1.8, 2.8, 1.5, 2.7}，图示它的离差平方：

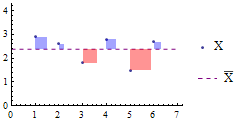
◇离差绝对值的平均值叫做平均差。

◇离差平方的平均值叫做方差。

%%%%%% Matlab代码: %%%%%%
X = [1, 2, 3, 4];
mu = mean(X); % 平均值2.5
dev = X - mu % 离差
% dev = -1.5000 -0.5000 0.5000 1.5000
mad(dev) % 平均差mean(abs(dev))，即 ans = 1

下图是离差绝对值与离差平方的图片效果比较，A.原图 B.平均值 C.离差 D.离差平方。C可以看作是A和B的差值。对照A、B可以看出，C、D中较亮的地方，正是A、B之间差异较大的部分，而较暗的地方则相反。C比D的层次更丰富一些，但D比C更容易看出哪些部分是差异特别大的，因为大部分和平均值相似的地方在D中都呈黑色。

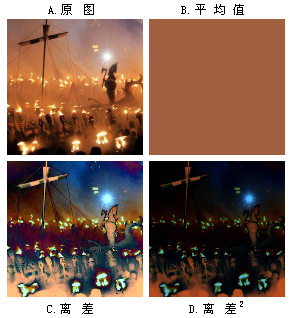
%%%%%% Matlab(上图的实现代码): %%%%%%
subplot(2,2,1);
img1 = im2single(imread('c:/a1.jpg'));
mu = mean(mean(img1)); % 求平均值
sz = size(img1);
imshow(img1); % 显示原图

subplot(2,2,2);
x = zeros(sz(1),sz(2),3); % 生成平均值图片
x(:,:,1) = mu(1,1,1);
x(:,:,2) = mu(1,1,2);
x(:,:,3) = mu(1,1,3);
imshow(x); % 显示平均值图

subplot(2,2,3);
imOut = abs(img1 - x) * 2; % 乘2是为了加强对比效果
imshow(imOut); % 显示离差图

subplot(2,2,4);
imOut = (img1 - x) .^ 2 * 2;
imshow(imOut); % 显示离差平方图

了解离差平方的这种特性，对于理解PCA人脸识别很重要。可以简单地理解为把离差平方压缩之后提取出来做为特征，生成特征脸。以此方法把要识别的人脸转换成特征脸，再和数据库中大量的特征脸样本一一比对，差别最小的就是要找的人。

PCA用的是协方差(离差x*离差y)，和上面的例子不太一样，后面的章节会讲到。

2.15 方差(Variance)

也称均方差(MSE, Mean Square Error)、误差(Error)，是离差平方的平均值。一个随机变量的方差描述的是它的离散程度，也反应了该变量与其期望值的差距。记作：s^2 或 σ^2 读法：σ是小写的∑(西格玛)。公式：

$$Var(X)=E[(x-\bar x)^2]$$
读作：方差 = 离差平方的期望值

举例说明，某次考试两个班的平均成绩都是70分，一班的同学大部分都在70分左右，没有不及格的；而二班有不少同学成绩是接近满分的，另有不少同学不及格。由此可见，单靠平均值来描述成绩是不够的，于是我们引入方差的概念，以此来描述成绩的波动程度(离散度)。如果方差很小，说明成绩比较稳定，如果方差很大则说明成绩的波动比较大。

样本方差公式：

$$Var(X)=s^2=\frac{\sum_{i=1}^n(x-\bar x)^2}{n-1}$$

除数为什么是n-1？实际工作中，我们往往只是对一部分样本进行抽查，样本的平均值不能代表总体的平均值，n-1是样本对总体的无偏估计。通俗地讲，n-1作除数可以禁止n=1的情况，即不允许只抽查一个样本；在样本很少的情况下，n-1促使方差变得较大；随着n的逐渐增大，样本方差将越来越接近总体方差。

%%%%%% Matlab代码: %%%%%%
var([1 2 3 4])
% ans = 1.6667

总体方差公式：

$$Var(X)=\sigma^2=\frac{\sum_{i=1}^n(x-\bar x)^2}{n}$$

对于总体样本的统计，可以直接用n作除数。

2.16 标准差(Std Dev, Standard Deviation)

也称标准方差、标准偏差、标准误差(RMSE)，是方差的算术平方根。由于方差是平方后的数据，实际工作中为了度量单位统一，常常会做开方处理，因此就有了标准差。方差和标准差是测度数据差异程度的最重要、最常用的指标。记作：s 或 σ，公式：

$$s=\sqrt {s^2}=\sqrt {\frac{\sum_{i=1}^n(x-\bar x)^2}{n-1}}$$

%%%%%% Matlab代码: %%%%%%
std([1 2 3 4])
% ans = 1.2910

下面是两张平均值相同的图片的中位数和标准差对比(灰度值范围0~255)：中位数(73<96)说明左图偏暗；左图的标准差(72)远大于右图(26)，说明左图的明暗对比非常强烈。

2.17 极差(Range)

也称全距、范围，是指一组数据的最大值减去最小值所得的结果。记作：r 或 ω 读法：ω是小写的Ω(欧米伽)。公式：

$$r=x_{max}-x_{min}$$
极差和标准差都可以描述一组数据的离散程度，极差是总体标准差的有偏估计值。

例：12 12 13 14 16 21这组数字的极差是：21(最大)-12(最小) = 9

%%%%%% Matlab代码: %%%%%%
range([12 12 13 14 16 21])
%

2.18 归一化(Normalization)

也称标准化，就是把一组数字按比例缩放到0~1或-1~1等符合标准的范围。归一化的数据有时也被称作纯量(标量,无向量,Scalar)。归一化会给数据处理带来很大方便。数据在归一化之后，将很容易地缩放至任何数值范围。公式：

$$x_{norm}=\frac{x-x_{min}}{range}=\frac{x-x_{min}}{x_{max}-x_{min}}$$
读作：归一值 = (当前值-最小值)/极差 = (当前值-最小值)/(最大值-最小值)

如果限定了范围(ymin~ymax)，公式为：

$$y = \frac{(y_{max}-y_{min})*(x-x_{min})}{(x_{max}-x_{min})} + y_{min}$$

例如0.1~0.9的范围：(0.9-0.1)*(x-min)/(max-min)+0.1

下图是一组数据的归一化前后对比。

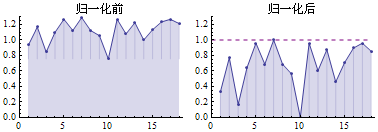
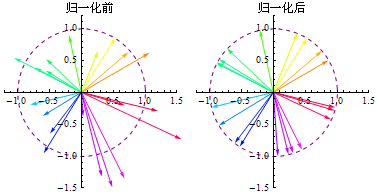
向量归一化之后，成为单位向量(Unit Vector)，这样可以只考虑方向不考虑长度。每个向量是单独归一化的，range取向量的长度。单位向量只关心方向而不关心长度(长度固定为1)，标量是只有大小没有方向。

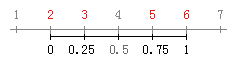
例：把5, 2, 6, 3这四个数归一化。

range = 6 – 2 = 4; norm = [(5-2)/4, (2-2)/4, (6-2)/4, (3-2)/4] = [0.75, 0, 1, 0.25]

%%%%%% Matlab代码: %%%%%%
a = [5, 2, 6, 3];

b = mapminmax(a, 0, 1) % 归一化到0~1之间
% b = 0.7500 0 1.0000 0.2500

c = mapminmax(a) % 归一化到-1~1之间
% c = 0.5000 -1.0000 1.0000 -0.5000

反归一化(Denormalization)就是按归一化时的比例还原数值。

% %%%%% Matlab代码: %%%%%%
a = [5, 2, 6, 3];
[c,PS] = mapminmax(a); % PS记录归一化时的比例
mapminmax('reverse', c, PS) % 利用PS反归一化
% ans = 5 2 6 3

2.19 统计可视化(Visualization)

自十八世纪后期数据图形学诞生以来，抽象信息的视觉表达手段一直被人们用来揭示数据及其他隐匿模式的奥秘。数据可视化试图通过利用人类的视觉能力，来搞清抽象信息的意思，从而放大了人类的认知能力。统计可视化以各种图表的形式来表现数据，帮助人们理解数据是如何分布的，并辅助与其它数据集和分布进行直观地对比。常见的统计图表有柱形图、条形图、折线图、散点图、饼形图、扇形图、环形图、雷达图、气泡图等，复杂些的有直方图、箱线图、分布图、树状图、网状图等。

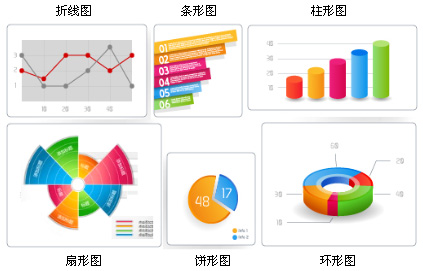
下图是Excel的图表工具，其中包含了大多数常用的统计图表。

参看：

二十大数据可视化工具点评

http://www.ctocio.com/hotnews/8874.html


阮一峰 – Google Chart API

http://www.ruanyifeng.com/blog/2007/12/google_chart_api.html

2.20 直方图(Histogram)

也称柱状图，是一种统计报告图，由一系列高度不等的纵向条纹表示数据分布的情况。

例1：有一堆零散无序的硬币，把硬币按面额的大小纵向排列起来，就成了直方图。

例2：图像的直方图，是根据每个像素点的灰度(亮暗度)来排列的。下图的灰度范围是0~7，0代表黑色，7代表白色，其它数字代表0~7之间不同深浅的灰度(Grayscale)。

按灰度从小到大的顺序排列起来，就成了图像直方图。

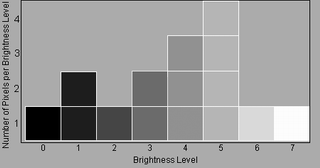
直方图统计的是像素的灰度，因此彩色图片要转成黑白图片(灰度图)，或把颜色的R、G、B通道分离再统计。Photoshop统计的灰度范围是0~255。

%%%%%% Matlab代码: %%%%%%
w = -6 + sqrt(10)*(randn(1,10000)); % 测试高斯分布效果的例子。
hist(w) % 直方图(柱状图)显示数据。
hist(w,50) % 直方图，显示单位：50。

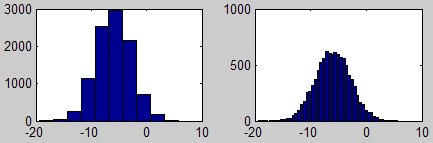
2.21 集合论(Set Theory)

也称集论，是研究集合的数学理论，包含了集合、元素和成员关系等最基本的数学概念。集合论加上逻辑和谓词演算构成了数学的公理化基础。集合论由俄国数学家康托尔(Cantor)在1873年创立。按现代数学观点，数学各分支的研究对象或者本身是带有某种特定结构的集合如群、环、拓扑空间，或者是可以通过集合来定义的(如自然数、实数、函数)。从这个意义上说，集合论可以说是整个现代数学的基础。

【集合(Set)】 – 是把一些确定的、可以区分的事物汇集到一起组成的一个整体。记作：A (使用大写字母来表示各种不同集合)

集合中的元素一般写在大括号里，集合的表示方法有两种：

1. 例举法 – 例如：A = {1, 2, 3, 4} 或 A = {a, 2, Fred} 在编程中常用中括号来代替大括号，并把集合称为数组(Array)，例如：A = [1, 2, 3, 4]

2. 描述法 – 元素和描述用竖线隔开，例如：B={x|x是偶数}

[注] 严格地说，集合和数组是不同的。集合中元素的排列顺序是随意的，但不能有重复的元素，而数组则相反。

【元素(Element)】 – 也称成员(Member)，是组成集合的每个事物。记作：x (一般是用小写字母来表示各种不同元素) 若x是集合A的元素，则x属于A。 记作：x∈A 读作：x属于A 英文：belong to (相反地，如果x不属于A，记作：x∉A )

【基数(Cardinal Number)】 – 也称元素数量、势(Cardinality)，是集合中元素的个数。基数可以是有限的，也可以是无限的。记作：|A| 例：A={1,2,3} 则|A|=3，如果两个集合的基数相等，称为等势，记作：A~B 或 |A|=|B|

【逻辑量词(Quantification)】 – 量词是谓词逻辑(Predicate Logic)的重要组成部分。

全称量词代表全部(For All)、所有、任何、任意的、每一个，记作：∀x 例：∀x∈R代表所有x都属于R(实数集)

存在量词代表存在(Exists)、有、有些、至少有一个，记作：∃x 例：∃x∈A代表存在一个x属于A

存在唯一的(Exists Unique)、只存在一个，记作：∃!x

【子集(Subset)】 – 若集合A中的所有元素都是集合B中的元素，则A是B的子集。记作：A⊆B 或 B⊇A 读作：A包含于B 或 B包含A 英文：B is contained in B; B contains A; inclusion; containment (可以理解为A≤B或B≥A) (不包含符号：⊈ 和 ⊉)

【真子集(Proper Subset)】 – 同子集，但A和B的内容不能相等。记作：A⊂B 或 B⊃A 读作：A真包含于B 或 B真包含A (可以理解为A








<










$\lt$
B或B>A) (不真包含符号：⊄ 和 ⊅)。

由于在不少文章中出现⊂和⊆混淆的情况，为了澄清概念，新版教材把真子集符号改为：⊊ 和 ⊋

【并集(Union)】 – 是由所有属于A或属于B的元素所组成的集合。记作：A∪B 逻辑符[选言命题]：A|B(A或者B)、A∨B(or,或) 读作：A并B 例：A={1,2,3} B={2,3,4} A∪B={1,2,3,4} (可以理解为A+B)

【交集(Intersection)】 – 是同时在集合A及B中出现的元素。记作：A∩B 逻辑符[联言命题]：A&B(A并且B)、A∧B(and,与) 读作：A交B 例：A={1,2,3} B={2,3,4} A∩B={2,3}

【对称差(Symmetric Difference)】 – 是指只在集合A及B中的其中一个出现，没有在其交集中出现的元素。记作：A△B、A⊕B 或 A⊖B 逻辑符[不相容选言命题]：A^B(要么A要么B)、A⊕B(xor,异或)、A⊻B 或 A B 例：A={1,2,3} U={2,3,4} A△B={1,4}

【空集(Empty Set)】 – 不含任何元素的集合称为空集。记作：Ø、Φ(读phi,拼音fai) 或 {}

【全集(Universe)】 – 也称论域、样本空间，是包含了所有的研究对象的集合。任何集合都不能大于全集，也不能小于空集。记作：U(大写的u)

【补集(Complement)】 – 也称差集(Difference)、余集、对立事件，有绝对补集和相对补集之分。符号为：A^C、A‘ 或 ∁A 逻辑符[负命题]：!A(非A)、¬A(not,非) 、~A 或

绝对补集(Absolute Complement) 是全集中所有不在集合A中的元素。符号为：∁uA 记作：A’=U\A

相对补集(Relative Complement) 是在集合A中，但不在集合B中的所有元素。记作：B*∩A=A\B 或 B*=A-B 例：A={1,2,3} B={2,3,4} A\B={1}

还有一种定义，把绝对补集称为补集(U\A)，把相对补集称为差集(A-B)。

【笛卡尔积(Cartesian Product)】 – 也称卡氏积、直积，是一个由所有可能的有序对(a,b)形成的集合，其中第一个物件是A的成员，第二个物件是B的成员。笛卡尔积是定义种种数学概念的基本手段之一。记作：A×B 例：{1,2}×{red,white}={(1,red), (1,white), (2,red), (2,white)}

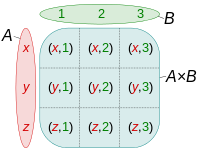
【幂集(Power Set)】 – 是指是以A的全部子集为元素的集合。记作：P(A)、ℙ(A) 、℘(A) 或 2^A。集合{1, 2} 的幂集为{

{}, {1}, {2}, {1,2}}, 子集数量刚好是|A|=2^2=4。

[注] 逻辑符[逻辑学名称]：是指布尔代数和逻辑学的对应符号。

常用数字集合符号表示：

– 自然数集(非负整数)：N

– 正整数集：N* 或 N+

– 整数集：Z

– 有理数集：Q

– 实数集：R

%%%%%% Matlab代码: %%%%%%
A = [1, 2, 3]; B = [2, 3, 4];

ismember(6, A) % 判断6是否属于A
% ans = 0 % 属于为1，不属于为0

union(A, B) % 求并集 A∪B
% ans = [1, 2, 3, 4]

intersect(A, B) % 求交集 A∩B
% ans = [2, 3]

setxor(A, B) % 对称差 A⊕B
% ans = [1, 5]

setdiff(A, B) % 求差集 A-B
% ans = [1]

A = [1, 2]; B = [3, 4];
[a,b] = meshgrid(A, B); % 求笛卡尔集 A×B
[a(:) b(:)]
% ans = [1 3; 1 4; 2 3; 2 4]

C = [1 2 1 5 6 2 3 3 3];
unique(C) % 删除数组中的重复元素
% ans = [1 2 3 5 6]

参看：《集合论基础》 –

http://www.doc88.com/p-747553918388.html

2.22 韦恩图(Venn Diagram)

也称文氏图，是用圆圈直观地表示集合及其重叠区域的图示。常常被用来帮助推导关于类/集合运算的一些规律，或帮助理解推导的过程。1880年，英国数学家约翰·韦恩(John Venn)在《论命题和推理的图表化和机械化表现》一文中首次采用固定位置的交叉环形式再加上阴影来表示逻辑问题，这一表示方法，令学术界的专家们都无比激动，直到今天，韦恩图在集合论和逻辑学中还占据着十分重要的位置。

1880年，英国数学家约翰·韦恩(John Venn)在《论命题和推理的图表化和机械化表现》一文中首次采用固定位置的交叉环形式再加上阴影来表示逻辑问题，这一表示方法，令学术界的专家们都无比激动，直到今天，韦恩图在集合论和逻辑学中还占据着十分重要的位置。本文前面集合论词条里的所有图形表示用的都是韦恩图。使用韦恩图，可以简单明了地表示出一些较为复杂的集合运算。

根据集合的数量，韦恩图还可以有三集合、四集合和五集合等多种形式。

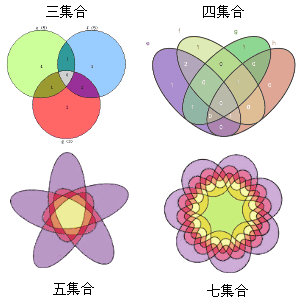
WolframAlpha(

http://www.wolframalpha.com

)提供自动生成韦恩图的功能。在搜索框输入表达式即可，例如输入：A⊻B⊻C⊻D。(Wolfram的⊻符号代表对称差△)

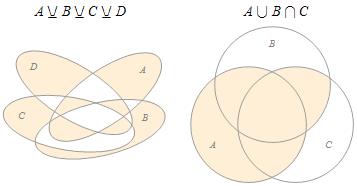
2.23 箱线图(Box Plot)

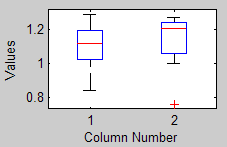
也称箱形图、盒式图、盒须图(Box-whisker Plot)、箱须图，是利用数据中的五个统计量：最小值、第1四分位数(25%)、中位数、第3四分位数(75%)与最大值来描述数据的一种方法，它可以粗略地看出数据是否具有有对称性，分布的分散程度等信息，可以用于多组数据的比较。

例1：有一组数据{0.93, 1.17, 0.84, 1.10, 1.27, 1.12, 1.29, 1.12, 1.06, 0.76, 1.27, 1.08, 1.22, 1.00, 1.13, 1.23, 1.27, 1.21}，画出它的箱线图。

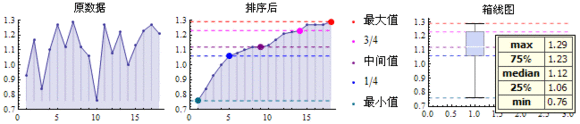
例2：根据5组数据画出箱线图。

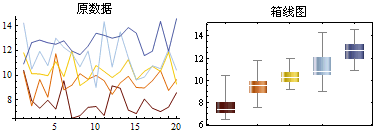
箱线图的作用：

1. 直观明了地识别多组数据中的异常值。

2. 判断多组数据的偏态和尾重。

3. 用于比较和分析多组数据的形状。

%%%%%% Matlab代码: %%%%%%
X = [0.93, 1.17, 0.84, 1.10, 1.27, 1.12, 1.29, 1.12, 1.06;
0.76, 1.27, 1.08, 1.22, 1.00, 1.13, 1.23, 1.27, 1.21];
boxplot(X*) % X为两组数据

参看：

《Matlab绘制箱线图》 –

http://blog.[

新浪].com.cn/s/blog_5fe5061101013lhd.html

《Excel绘制箱线图》 –

http://wiki.mbalib.com/wiki/

箱线图

2.24 映射(Map)

也称投影(Projection)，集合A,B的笛卡尔积A×B的子集叫做A到B的映射。映射可以理解为“影子”，一个人可以有一个或多个影子，也可以没有影子。影子总是与光源相对应，在某一确定光源的照射下，每个人都会有不同的影子。同样，集合A里的元素，在集合B里也会有影子，光源可以理解为产生投影的函数。

记作：f:A→B 或 f:A↦B

对于函数的概念，通过映射可以给出更为精确的定义：f:A→B (∀x ∈A, ∃!y∈B) 读作：对于集合A中所有的元素x，在集合B中都有唯一的元素y与之对应。

函数的映射有三种常见的情况：单射(Injection, one to one)、满射(Surjective, onto)和双射(bijective, one-to-one correspondence)。单射是一对一，满射是指Y的每个指都有X的对应，双射代表既单射又满射的情况，双射要求A、B等势(数量相等)。

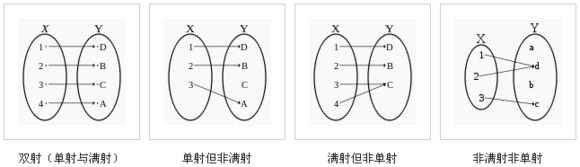
[注] A→B、A⇒B 或 A=>B 代表蕴涵(Imply)、命题逻辑的假言命题、能够推出、如果…那么(If)、只有…才(If only)等含义。

A↔B 或 A⇔B 代表等价(Equivalent)、命题逻辑的充分必要条件假言命题、当且仅当(Iff, If and only if)等含义。

而f:A→B 代表集合映射、从…到…，“→”代表函数。

2.25 模糊集合(Fuzzy Set)

也称模糊集，是传统集合论的扩充版，它的主要特点是模糊了集合的边界。对于传统集合论，x要么属于A，要么不属于A，只有这两种情况；而模糊集合多出一个隶属度的概念，隶属度是个介于0~1的数值(和概率有点像)，因此，x可以100%隶属于A，也可以20%隶属于A。模糊集合给传统二值分类法加了一个度，对冷热、轻重、高矮、长短等属性值的分辨，由阈值变成了灰度。

定义：一个模糊集合A={U, μ} (代表A由U和μ两个成份组成，U代表一个全集)，μ:U→[0,1] (表示μ是从U到[0,1]的映射，也就是说全集U中的每一个元素，都有一个输出值范围为0~1之间的函数μ与之对应)。对于∀x∈U (U中的每个元素x) ，函数μ(x)叫做模糊集合A的隶属函数(Membership Function)，μ(x)的输出值叫做x的隶属度(Membership Degree, Grade)。

隶属函数记作：μ(x)、μA(x)、A(x)、m(x) 或 M(x)

[注] 模糊集合中文教程一般把“全集”称为“论域”，英文资料常把“元素(Element)”称为“成员(Member)”。

模糊数学的概念是加利福尼亚大学控制论专家扎德(Lotfi. A. Zadeh)于1965年首先提出的。英语中的“模糊(Fuzzy)”一词是有些贬义的，所以这种理论在英语国家不太受欢迎，推动模糊控制理论发展的主要是日、韩等亚洲国家，中国也有份。

问题的提出：人类的自然语言中存在大量的模糊词汇，假如一个厨师指导你如何烘烤出完美的奶酪面包，他也许会这么说：

1. 把面包切成
   
   中等厚度
   
   的两片。
2. 把平底锅的加热按钮调到
   
   高档
   
   。
3. 烤面包切片的一面，直到它变成
   
   金黄色的
   
   。
4. 把面包切片翻过来，并添加
   
   大量
   
   的奶酪。
5. 把面包切片放回原处继续烤，直到上面的奶酪变成
   
   微褐色
   
   。
6. 拿走面包切片，洒上
   
   少量
   
   的黑胡椒粉，并开始吃。

用粗体显示的字都是一些模糊术语。我们遵循这些指令，就可以做出一份美味的快餐。那么我们对一个可编程的机器人下达这些指令可以吗？有编程经验的人都知道这是不行的。编程时，我们必须明确指定“中等厚度”到底有多厚，“高档”具体是几档，“金黄色”的RGB值是多少等等，总之是要明确的数值或数值范围才行。在给出明确数字的过程中，我们的大脑根据经验把这些模糊的词汇转换成了具体的数值。想象一下，如果计算机可以模仿我们的大脑，直接对模糊的词汇进行处理，自动完成这一转换过程并执行命令那该有多酷！

为此，模糊数学迈出了精妙的一步，它制定了一种模糊词汇的转换格式和一系列的模糊推理方式，为解决这类问题做出很大的贡献。然而，对于如何自动设置模糊词汇的数值范围(自动生成隶属函数)，包括如何采集数据训练模糊范围、如何自适应模糊数值、如何调整和纠错等一系列问题，它还存在着很大欠缺。

扎德：“我们一般认为数学应当是精确的，很难和模糊概念联系在一起。但事实上实际生活中，特别是人的问题，更多使用的是模糊思维。我觉得需要解决这个问题，应该把数学和生活联系起来，就去找一些数学家来聊。结果他们都不感兴趣，我只好自己来研究。这个研究从1964年开始，1965年发表了第一篇文章《模糊集合》。就这么开始了。”

例：对人的年龄定义，16岁之前为年幼，16岁到32岁的年龄段为年轻，传统集合的描述(Def1)：年幼={x|1








<










$\lt$
x<16}, 年轻={x|16








<










$\lt$
x<32}，如果一个孩子只有3岁(a=3)，可以说：a∈年幼, a∉年轻。

其实年幼和年轻是可以有交集的，那么重新定义(Def2)：年幼={x|1








<










$\lt$
x<20}, 年轻={x|10








<










$\lt$
x<32}，此时：青少年=年幼∩年轻={x|10








<










$\lt$
x<20}，如果一个人16岁(a=16)，那么可以说：a∈(既)年幼, a∈(又)年轻, a∈(是)青少年。

以上都是用传统的清晰集合来描述的，在模糊数学中，把这种清晰集合称为清脆集合(Crisp Set)。清脆集合忽略了我们平时比较在乎的程度问题，按Def2的定义如果说18岁年幼或13岁年轻都觉得有些不恰当，但如果说13岁是非常年轻，18岁是比较年轻似乎感觉更恰当一些。为解决此问题，我们引入模糊集合的处理方式。

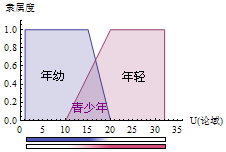
对于非常、很、比较、有点等程度副词，模糊集合用了一个0~1之间的数字来描述。比如11岁可以用年轻度0.1来表示，12岁为年轻度0.2，13岁0.3……直到20岁以后年轻度为1，10岁以前年轻度为0，可以用下面这个表达式(Zadeh 记法)来表示：

$$A=\frac{0}{10}+\frac{0.1}{11}+\frac{0.2}{12}+...+\frac{1}{20}$$

注意：Zadeh记法的+号和分数线不是运算符，只是分隔符，相当于逗号。

模糊集合除了Zadeh记法，还有两种常见的表示法。

1. 序偶法：A = {(10,0), (11,0.1), (12,0.2), … , (20,1)}

2. 向量法：A = (0, 0.1, 0.2,…,1)

从上面的Zadeh表达式中可以看出，年轻度(分子)和年龄(分母)之间有很明显的函数关系，年轻度 = A(x) = (年龄-10)/10。函数A(x)称为隶属函数，年轻度为隶属度，年龄为论域(全集)中的元素。

也许你对此例的年幼、年轻是几岁到几岁的定义很不认同，那没关系，因为你完全可以凭着的自己的感觉来重新定义，也可以反复调整。对于隶属函数的选择和设定没有绝对的标准，主要是由程序设计者的经验和偏好来决定，具有很强的主观性。当然这种主观性也是导致它难以被数学界接受的重要原因。

隶属函数既可以是线性函数，也可以是曲线函数；函数图形可以是梯形，也可以是三角形、钟形、马蹄形等多种形式。下图是Matlab中支持的11种隶属函数形状(mfdemo)。

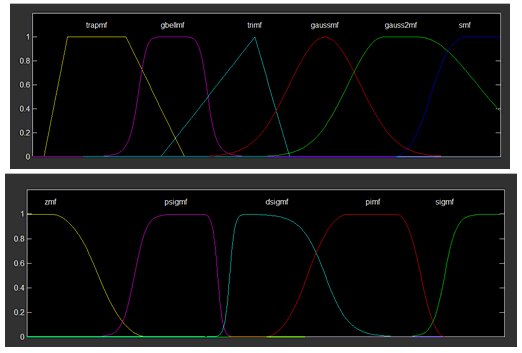
模糊集合也有一套求交集、并集、补集的集合运算法则，这套法则是模糊逻辑和模糊推理的基础。

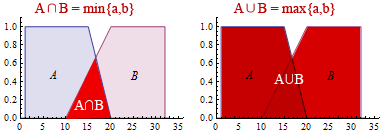
模糊推理完成时，会有一步清晰化(去模糊)的运算，即把最终的模糊运算结果(例如上图的红色区域)转换为一个具体数值(期望值)，可视为求这个结果区域的平均值。整个流程是这样的：输入→模糊化→模糊规则(推理)→去模糊→输出。

表现两组事物相似度的对比关系，可以使用模糊矩阵。{苹果, 球, … , 四棱锥}7个对象，用传统的布尔矩阵只能表示它们是相似(1)还是不似(0)，而模糊矩阵用来表示它们的相似度。

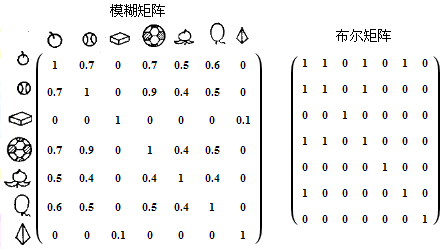
模糊数学是一门新兴学科，最早是应用在自动控制技术领域，后来在信息检索、医学、生物学、气象学、结构力学、心理学等各个领域都展开了广泛的应用，然而模糊数学最重要的应用领域是计算机智能，不少人认为它与新一代计算机的研制有密切的联系。

模糊数学还远没有成熟，人们对它还存在着各种不同的意见和看法，不过它也存在很大的拓展空间，有很大的潜力，有待大家的进一步深入完善。

参看：

《模糊集合2.ppt》(不错的模糊推理教程) –

http://www.docin.com/p-515261417.html


《模糊集合的基本概念与模糊关系》(模糊矩阵教程) –

http://wenku.baidu.com/view/f34802175f0e7cd18425365c.html


《游戏人工智能编程案例精粹》 第10章 模糊逻辑

2.26 排列&组合(Permutation & Combination)

排列：从n个元素中，抽取r个元素组成新的集合，不用按顺序抽取。也称置换。

组合：从n个元素中，抽取r个元素组成新的集合，要按顺序抽取。

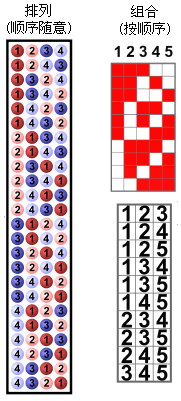
排列符号：P(n,r) 或











P








n






r










,






n










P








r







,


n





P








r















$P_r^n,^nP_r,n P_r$

组合符号：C(n,r) 或











C








n






r










,






n










C








r







,


n





C








r















$C_r^n,^nC_r,n C_r$

排列公式：

$$P_r^n=\frac{n!}{(n-r)!}$$

组合公式：

$$P_r^n=\frac{n!}{(n-r)!r!}$$

公式中，n和r代表从n个元素中取出r个元素，P(n,r)和C(n,r)代表组成所有排列或组合的可能性数量，!代表阶乘。

[注] 某些教材用A(Arrangement)表示排列，用k表示r。

例：从{a,b,c,d}这4个元素(n=4)的集合里挑出两个元素(r=2)，一共可以组成多少个排列和组合？

排列：{a,b,c,d}在不按顺序排列的情况下，有{a,b}, {a,c}, {a,d}, {b,a}, {b,c}, {b,d}, {c,a}, {c,b}, {c,d}, {d,a}, {d,b}, {d,c}，共12种排列。

数量为：P(4,2) = 4!/(4-2)! = (4*3*2*1)/(2*1) = 4*3 = 12

组合：{a,b,c,d}在按顺序排列的情况下，有{a,b}, {a,c}, {a,d}, {b,c}, {b,d}, {c,d}, ，共6种组合。

数量为：C(4,2) = 4!/(2!*(4-2)!) = (4*3)/(2*1) = 6

注意：实际计算时，不用除以(n-r)!，例如P(100,3) = 100*99*98，从100开始往下乘3个数即可。

%%%%%% Matlab代码: %%%%%%
perms([*abc*]) % 列举全部排列，支持字符串和行向量
% ans = [cba cab bca bac abc acb]*

n = 7; r = 3; % 求排列数，C = n!/(n–r)!
P = prod(n-r+1:n) % C = 7!/(7-3)! = 7*6*5 = 210;
% P = 210

C = nchoosek(4, 2) % 求组合数(n=4，r=2)，C = n!/(r!*(n–r)!)
% C = 6

nchoosek([*abcd*], 2) % n=行向量，r=2，列举全部组合
% ans = [ab ac ad bc bd cd]*

C = combntns([*abcd*], 2) % n为向量时，combntns同nchoosek
% ans = [ab ac ad bc bd cd]* (同nchoosek)