博客

题目描述

给出一个有向图G=(V, E)，和一个源点v0∈V，请写一个程序输出v0和图G中其它顶点的最短路径。只要所有的有向环都是正的，我们就允许图的边有负值。顶点的标号从1到n（n为图G的顶点数）。

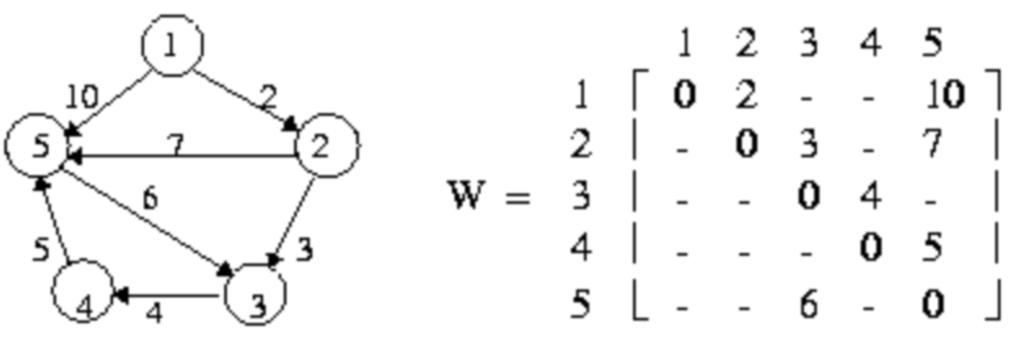
输入格式：

第1行：一个正数n（2<=n<=80），表示图G的顶点总数。

第2行：一个整数，表示源点v0（v0∈V，v0可以是图G中任意一个顶点）。

第3至第n+2行，用一个邻接矩阵W给出了这个图。

输出格式：

共包含n-1行，按照顶点编号从小到大的顺序，每行输出源点v0到一个顶点的最短距离。每行的具体格式参照样例。

输入样例：

5

1

0 2 – – 10

– 0 3 – 7

– – 0 4 –

– – – 0 5

– – 6 – 0

输出样例：

(1 -> 2) = 2

(1 -> 3) = 5

(1 -> 4) = 9

(1 -> 5) = 9

【解题分析】

经典的最短路模版题，求单源点最短路问题，使用dijkstra算法或者bellman-ford算法都可以。这里使用的是floyd。本题数据输入要做一些处理，混合了数字和字符，可以使用字符串转换处理解决。参考代码中使用了scanf的格式输入来解决。

【参考代码】floyd实现

#include<iostream>
#include<cstdio>
#include<string>
using namespace std;
const long long oo=1e16;
long long mp[100][100];
int n,v;
int main(){
	scanf("%d%d",&n,&v);
	for(int i=1;i<=n;i++){
		for(int j=1;j<=n;j++){
			long long x; 
			if(scanf("%lld",&x)) mp[i][j]=x;  //奇怪的输入 
			else mp[i][j]=oo;
		}
	}
	for(int k=1;k<=n;k++)
		for(int i=1;i<=n;i++)
			for(int j=1;j<=n;j++)
				mp[i][j]=min(mp[i][j],mp[i][k]+mp[k][j]);
	for(int i=1;i<=n;i++)
		if(i!=v)
			printf("(%d -> %d) = %lld\n",v,i,mp[v][i]);
	return 0; 
}