Optimization Algorithms
-
Using the notation for mini-batch gradient descent. To what of the following does
a[
2
]
{
4
}
(
3
)
a^{[2]\lbrace 4 \rbrace(3)}
a
[
2
]
{
4
}
(
3
)
correspond?
-
The activation of the third layer when the input is the fourth example of the second mini-batch. -
The activation of the second layer when the input is the third example of the fourth mini-batch. -
The activation of the fourth layer when the input is the second example of the third mini-batch. -
The activation of the second layer when the input is the fourth example of the third mini-batch.
-
Which of these statements about mini-batch gradient descent do you agree with?
-
You should implement mini-batch gradient descent without an explicit for-loop over different mini-batches so that the algorithm processes all mini-batches at the same time (vectorization). -
Training one epoch (one pass through the training set) using mini-batch gradient descent is faster than training one epoch using batch gradient descent. -
When the mini-batch size is the same as the training size, mini-batch gradient descent is equivalent to batch gradient descent.
(
解释: Batch gradient descent uses all the examples at each iteration, this is equivalent to having only one mini-batch of the size of the complete training set in mini-batch gradient descent.
)
-
Why is the best mini-batch size usually not 1 and not m, but instead something in-between? Check all that are true.
-
If the mini-batch size is 1, you lose the benefits of vectorization across examples in the mini-batch. -
If the mini-batch size is m, you end up with stochastic gradient descent, which is usually slower than mini-batch gradient descent. -
If the mini-batch size is 1, you end up having to process the entire training set before making any progress. -
If the mini-batch size is m, you end up with batch gradient descent, which has to process the whole training set before making progress.
-
While using mini-batch gradient descent with a batch size larger than 1 but less than m, the plot of the cost function JJ looks like this:
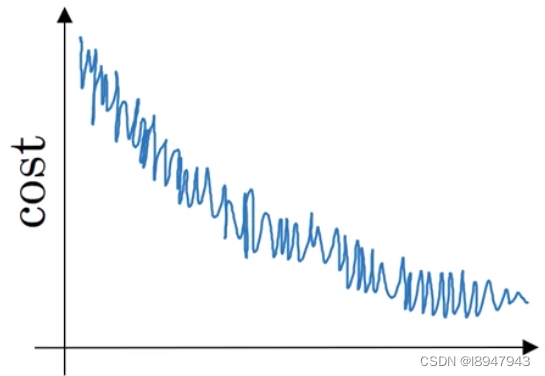
You notice that the value of
JJ
J
is not always decreasing. Which of the following is the most likely reason for that?
-
In mini-batch gradient descent we calculate
J(
y
^
{
t
}
,
y
{
t
}
)
)
J(\hat{y} ^{\{t\}} ,{y} ^{\{t\}} ))
J
(
y
^
{
t
}
,
y
{
t
}
))
thus with each batch we compute over a new set of data. -
A bad implementation of the backpropagation process, we should use gradient check to debug our implementation. -
You are not implementing the moving averages correctly. Using moving averages will smooth the graph. -
The algorithm is on a local minimum thus the noisy behavior.
(
解释:Yes. Since at each iteration we work with a different set of data or batch the loss function doesn’t have to be decreasing at each iteration.
)
-
Suppose the temperature in Casablanca over the first two days of January are the same:
Jan 1st:
θ1
=
1
0
o
C
\theta_1 = 10^o C
θ
1
=
1
0
o
C
Jan 2nd:
θ2
=
1
0
o
C
\theta_2 = 10^oC
θ
2
=
1
0
o
C
(We used Fahrenheit in the lecture, so we will use Celsius here in honor of the metric world.)
Say you use an exponentially weighted average with
β=
0.5
\beta = 0.5
β
=
0.5
to track the temperature:
v0
=
0
v_0 = 0
v
0
=
0
,
vt
=
β
v
t
−
1
+
(
1
−
β
)
θ
t
v_t = \beta v_{t-1} +(1-\beta)\theta_t
v
t
=
β
v
t
−
1
+
(
1
−
β
)
θ
t
. If
v2
v_2
v
2
is the value computed after day 2 without bias correction, and
v2
c
o
r
r
e
c
t
e
d
v_2^{corrected}
v
2
correc
t
e
d
is the value you compute with bias correction. What are these values? (You might be able to do this without a calculator, but you don’t actually need one. Remember what bias correction is doing.)
-
v2
=
10
v_2=10
v
2
=
10
,
v2
c
o
r
r
e
c
t
e
d
=
10
v^{corrected}_{2}=10
v
2
correc
t
e
d
=
10
-
v2
=
7.5
v_2=7.5
v
2
=
7.5
,
v2
c
o
r
r
e
c
t
e
d
=
7.5
v^{corrected}_{2}=7.5
v
2
correc
t
e
d
=
7.5
-
v2
=
7.5
v_2=7.5
v
2
=
7.5
,
v2
c
o
r
r
e
c
t
e
d
=
10
v^{corrected}_{2}=10
v
2
correc
t
e
d
=
10
-
v2
=
10
v_2=10
v
2
=
10
,
v2
c
o
r
r
e
c
t
e
d
=
7.5
v^{corrected}_{2}=7.5
v
2
correc
t
e
d
=
7.5
-
Which of the following is true about learning rate decay?
-
The intuition behind it is that for later epochs our parameters are closer to a minimum thus it is more convenient to take smaller steps to prevent large oscillations. -
We use it to increase the size of the steps taken in each mini-batch iteration. -
The intuition behind it is that for later epochs our parameters are closer to a minimum thus it is more convenient to take larger steps to accelerate the convergence. -
It helps to reduce the variance of a model.
(
解释:Reducing the learning rate with time reduces the oscillation around a minimum.
)
-
You use an exponentially weighted average on the London temperature dataset. You use the following to track the temperature:
vt
=
β
v
t
−
1
+
(
1
−
β
)
θ
t
v_{t} = \beta v_{t-1} + (1-\beta)\theta_t
v
t
=
β
v
t
−
1
+
(
1
−
β
)
θ
t
. The yellow and red lines were computed using values
be
t
a
1
beta_1
b
e
t
a
1
and
be
t
a
2
beta_2
b
e
t
a
2
respectively. Which of the following are true?
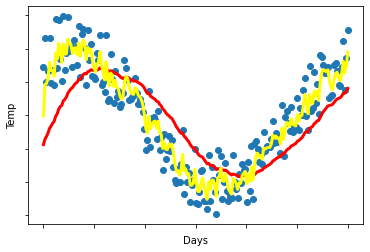
-
β1
<
β
2
\beta_1<\beta_2
β
1
<
β
2
-
β1
=
β
2
\beta_1=\beta_2
β
1
=
β
2
-
β1
>
β
2
\beta_1>\beta_2
β
1
>
β
2
-
β1
=
0
,
β
2
>
0
\beta_1=0,\beta_2>0
β
1
=
0
,
β
2
>
0
(
解释:越向右越平滑,β越大
)
-
Consider the figure:
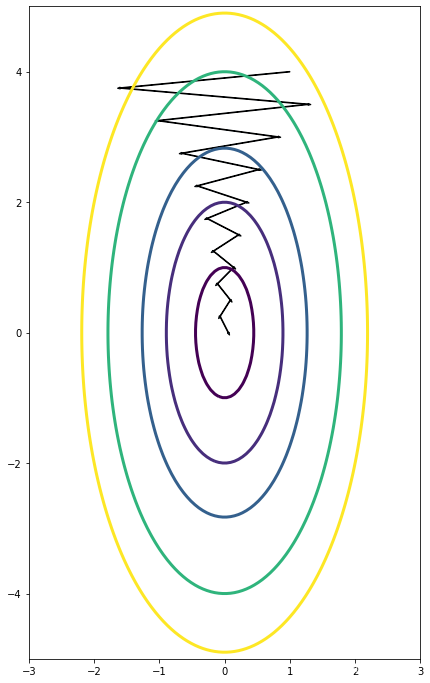
Suppose this plot was generated with gradient descent with momentum
β=
0.01
\beta = 0.01
β
=
0.01
. What happens if we increase the value of
β\beta
β
to 0.1?
-
The gradient descent process starts oscillating in the vertical direction. -
The gradient descent process starts moving more in the horizontal direction and less in the vertical. -
The gradient descent process moves less in the horizontal direction and more in the vertical direction. -
The gradient descent process moves more in the horizontal and the vertical axis.
(
解释:随着β增大,走的步伐跨度越大,振幅越小,The use of a greater value of β causes a more efficient process thus reducing the oscillation in the horizontal direction and moving the steps more in the vertical direction.
)
-
Suppose batch gradient descent in a deep network is taking excessively long to find a value of the parameters that achieves a small value for the cost function
J(
W
[
1
]
,
b
[
1
]
,
.
.
.
,
W
[
L
]
,
b
[
L
]
)
\mathcal{J}(W^{[1]},b^{[1]},…,W^{[L]},b^{[L]})
J
(
W
[
1
]
,
b
[
1
]
,
…
,
W
[
L
]
,
b
[
L
]
)
. Which of the following techniques could help find parameter values that attain a small value for
J\mathcal{J}
J
? (Check all that apply)
-
Normalize the input data.
(解释:
Yes. In some cases, if the scale of the features is very different, normalizing the input data will speed up the training process.
) -
Try better random initialization for the weights
(解释:
Yes. As seen in previous lectures this can help the gradient descent process to prevent vanishing gradients.
) -
Add more data to the training set. -
Try using gradient descent with momentum.
(解释:
Yes. The use of momentum can improve the speed of the training. Although other methods might give better results, such as Adam.
)
-
Which of the following are true about Adam?
-
Adam can only be used with batch gradient descent and not with mini-batch gradient descent. -
The most important hyperparameter on Adam is
ϵϵ
ϵ
and should be carefully tuned. -
Adam combines the advantages of RMSProp and momentum. -
Adam automatically tunes the hyperparameter
αα
α
.
(解释:
Precisely Adam combines the features of RMSProp and momentum that is why we use two-parameter
β1
β1
β
1
and
β2
β2
β
2
, besides
ϵϵ
ϵ
.
)