1.希尔排序
希尔排序是插入排序的一种,又称“缩小增量排序”,是插入排序算法的一种更高效的改进版本。
排序原理:
-
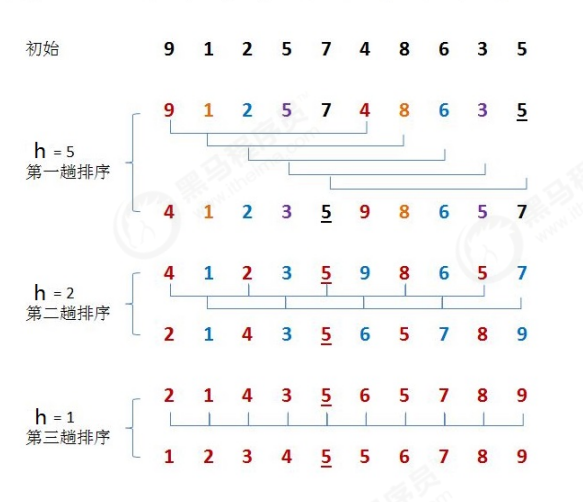
选定一个增长量h(可以为数组长度一半开始),按照增长量h作为数据分组的依据,对数据进行分组;
-
对分好组的每一组数据完成插入排序;
-
减小增长量,最小减为1,重复第二步操作。
//希尔排序
public static void sort(int[] arr) {
//增长量
int h = arr.length / 2;
while (h > 0) {
for (int i = h; i < arr.length; i++) {
int j = i, temp = arr[j];
while (j - h >= 0 && temp < arr[j - h]) {
//数组后退
arr[j] = arr[j - h];
j -= h;
}
//向前交换插入
arr[j] = temp;
}
//每次将分隔量减半
h /= 2;
}
}
2.快速排序
快速排序是对冒泡排序的一种改进。它的基本思想是:通过一趟排序将要排序的数据分割成独立的两部分,其中一 部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序 过程可以递归进行,以此达到整个数据变成有序序列。
排序原理:
-
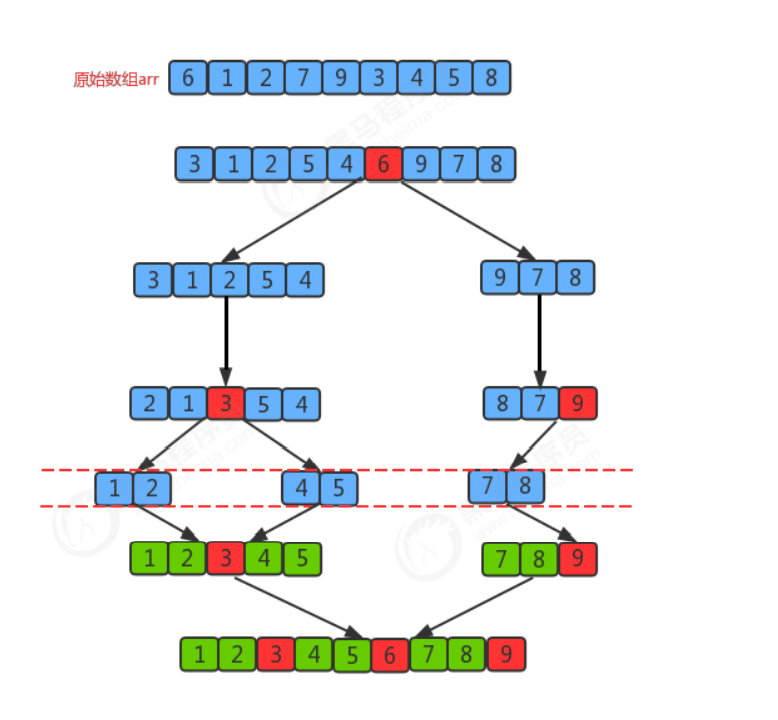
首先设定一个分界值,通过该分界值将数组分成左右两部分;
-
将大于或等于分界值的数据放到到数组右边,小于分界值的数据放到数组的左边。此时左边部分中各元素都小于 或等于分界值,而右边部分中各元素都大于或等于分界值;
-
然后,左边和右边的数据可以独立排序。对于左侧的数组数据,又可以取一个分界值,将该部分数据分成左右两 部分,同样在左边放置较小值,右边放置较大值。右侧的数组数据也可以做类似处理。
-
重复上述过程,可以看出,这是一个递归定义。通过递归将左侧部分排好序后,再递归排好右侧部分的顺序。当 左侧和右侧两个部分的数据排完序后,整个数组的排序也就完成了。
//快速排序
public static void sort(int[] arr, int left, int right) {
int leftTemp = left, rightTemp = right;
int center = arr[right - (right - left) / 2];
while (left < right) {
//左边找到比中间值大的停止循环,如果没有则到center退出
while (arr[left] < center) {
left += 1;
}
//右边找到比中间值小的停止循环,如果没有则到center退出
while (arr[right] > center) {
right -= 1;
}
//结束while循环
if (left >= right) {
break;
}
//进行左右交换
int temp = arr[left];
arr[left] = arr[right];
arr[right] = temp;
//避免左边值等于中间值,将中间值交换过去,要将右边指针左移一位,避免死循环
if (arr[left] == center) {
right -= 1;
}
//避免右边值等于中间值,将中间值交换过去,要将左边指针左移一位,避免死循环
if (arr[right] == center) {
left += 1;
}
}
//避免栈溢出
if (left == right) {
left += 1;
right -= 1;
}
//向左递归
if (leftTemp < right) {
sort(arr, leftTemp, right);
}
//向右递归
if (left < rightTemp) {
sort(arr, left, rightTemp);
}
}
3.归并排序
归并排序是建立在归并操作上的一种有效的排序算法,该算法是采用分治法的一个非常典型的应用。将已有序的子 序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序 表,称为二路归并。
排序原理:
-
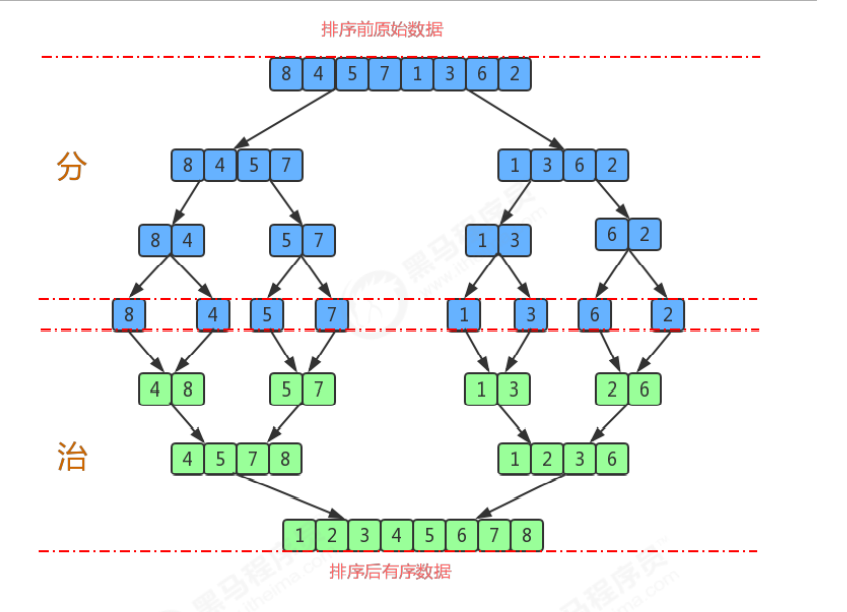
尽可能的一组数据拆分成两个元素相等的子组,并对每一个子组继续拆分,直到拆分后的每个子组的元素个数是 1为止。
-
将相邻的两个子组进行合并成一个有序的大组;
-
不断的重复步骤2,直到最终只有一个组为止。
//归并排序
public static void sort(int[] arr, int left, int right) {
if (left < right) {
//创建临时数组
int[] temp = new int[right - left + 1];
int center = left + (right - left) / 2; //获取中间索引
//向左递归
sort(arr, left, center);
//向右递归
sort(arr, center + 1, right);
sort(arr, left, center, right, temp);
}
}
/**
* 具体排序合并方法
*
* @param arr 排序数组
* @param left 左边界
* @param center 中间分界线
* @param right 右边界
* @param temp 临时数组,用来copy和排序数组
*/
private static void sort(int[] arr, int left, int center, int right, int[] temp) {
//定义左指针,左终点为center,并且定义右指针
int leftTemp = left, rightTemp = center + 1;
//临时数组遍历指针
int tempStart = 0;
//对俩边数组比较遍历,丢入临时数组中(结束条件为左边指针或者右边指针一个遍历结束)
while (leftTemp <= center && rightTemp <= right) {
//判断丢入临时数组
if (arr[leftTemp] > arr[rightTemp]) {
temp[tempStart] = arr[rightTemp];
rightTemp++;
tempStart++;
} else {
temp[tempStart] = arr[leftTemp];
leftTemp++;
tempStart++;
}
}
//遍历左边可能剩余的数组元素
while (leftTemp <= center) {
temp[tempStart] = arr[leftTemp];
leftTemp++;
tempStart++;
}
//遍历右边可能剩余的数组元素
while (rightTemp <= right) {
temp[tempStart] = arr[rightTemp];
rightTemp++;
tempStart++;
}
//temp数组指针从头开始
tempStart = 0;
//将temp数组排序好的数组copy到要排序的数组中
for (int i = left; i <= right; i++) {
arr[i] = temp[tempStart++];
}
}