博客

1 多元线性回归的基本原理

线性回归是机器学习中最简单的回归算法，多元线性回归指的就是一个样本有多个特征的线性回归问题。对于一个有



n

n






n





个特征的样本



i

i






i





而言，它的回归结果可以写作一个几乎人人熟悉的方程:









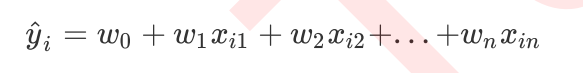
先定义了

损失函数

，然后通过最小化损失函数或损失函数的某种变化来将求解参数向量，以此将单纯的求解问题转化为一个最优化问题。在多元线性回归中，我们的损失函数如下定义：

2 最小二乘法求解多元线性回归的参数

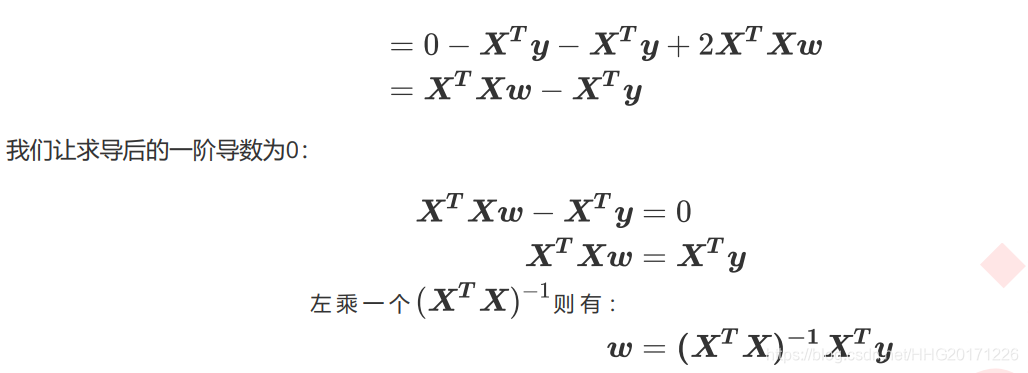
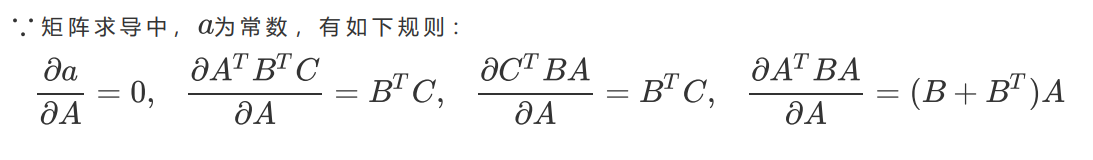
到了这里，我们希望能够将 留在等式的左边，其他与特征矩阵有关的部分都放到等式的右边，如此就可以求出



w

w






w





的最优解了。这个功能非常容易实现，只需要我们左乘



X

T

X

X^TX







X










T









X





的逆矩阵就可以。

在这里，逆矩阵存在的充分必要条件是特征矩阵不存在多重共线性


linear_model.LinearRegression


使用普通最小二乘法的线性回归

class sklearn.linear_model.LinearRegression (fit_intercept=True, 
											normalize=False, 
											copy_X=True, 
											n_jobs=None
									)

参数：

• 
fit_intercept

  :布尔值，可不填，默认为True
  
  是否计算此模型的截距。如果设置为False，则不会计算截距
• 
normalize

  :布尔值，可不填，默认为False
  
  当fit_intercept设置为False时，将忽略此参数。如果为True，则特征矩阵X在进入回归之前将会被减去均值（中心化）并除以L2范式（缩放）。如果你希望进行标准化，请在fit数据之前使用preprocessing模块中的标准化专用类StandardScaler
• 
copy_X

  :布尔值，可不填，默认为True
  
  如果为真，将在X.copy()上进行操作，否则的话原本的特征矩阵X可能被线性回归影响并覆盖
• 
n_jobs

  :整数或者None，可不填，默认为None
  
  用于计算的作业数。只在多标签的回归和数据量足够大的时候才生效。除非None在joblib.parallel_backend上下文中，否则None统一表示为1。如果输入 -1，则表示使用全部的CPU来进行计算。
  
  线性回归的类可能是我们目前为止学到的最简单的类，仅有四个参数就可以完成一个完整的算法。并且看得出，这些参数中并没有一个是必填的，更没有对我们的模型有不可替代作用的参数。这说明，线性回归的性能，往往取决于数据本身，而并非是我们的调参能力，线性回归也因此对数据有着很高的要求。幸运的是，现实中大部分连续型变量之间，都存在着或多或少的线性联系。所以线性回归虽然简单，却很强大。
  
  (sklearn中的线性回归可以处理多标签问题，只需要在fit的时候输入多维度标签就可以了。)
  
  代码：

#1. 导入需要的模块和库

from sklearn.linear_model import LinearRegression as LR
from sklearn.model_selection import train_test_split
from sklearn.model_selection import cross_val_score
from sklearn.datasets import fetch_california_housing as fch #加利福尼亚房屋价值数据集
import pandas as pd


 #2. 导入数据，探索数据
housevalue = fch() #会需要下载，大家可以提前运行试试看
X = pd.DataFrame(housevalue.data) #放入DataFrame中便于查看
y = housevalue.target
print(X.shape)

X.columns = housevalue.feature_names


#3. 分训练集和测试集
Xtrain, Xtest, Ytrain, Ytest = train_test_split(X,y,test_size=0.3,random_state=420)

#重新建立索引
for i in [Xtrain, Xtest]:
    i.index = range(i.shape[0])

#如果希望进行数据标准化，还记得应该怎么做吗？
#先用训练集训练标准化的类，然后用训练好的类分别转化训练集和测试集


#4. 建模
reg = LR().fit(Xtrain, Ytrain)
yhat = reg.predict(Xtest)


#5. 探索建好的模型
#reg.coef_ 参数w1,w2.....wn
print(reg.coef_)

#截距  reg.intercept_
print(reg.intercept_)