Python数值积分
数值积分
相对微分而言,积分的难度要大得多。虽然有很多可以用解析方法来计算和的积分,大部分情况下,我们需要使用数值的方法。
连续函数以及有限积分域的积分在单一维度上可以有效计算,但是对于带奇点或无限积分域的可积函数,即使是一维数值积分也很困难。二维积分和多重积分可以通过重复一维积分来进行计算,但是计算量会随着维度上升急剧增长。高维积分需要使用蒙特卡罗采样算法等技术。
除了进行数值计算外,积分还有很多其他同途:
-
积分方程
(含有未知函数的积分进行运算的方程)经常在科学和工程中使用。积分方程一般很难求解,通常可以将它们离散化,然后转换为线性方程组。 -
积分变换
,可用于不同域之间的函数和方程变换,例如傅里叶变换。
导入模块
本部分我们将主要使用SciPy的integrate模块进行数值积分。针对高精度浮点运算的需要,我们也会搭配使用SymPy和
mpmath
进行任意精度积分。
import matplotlib.pyplot as plt
import matplotlib as mpl
import numpy as np
from scipy import integrate
import sympy
import mpmath
%reload_ext version_information
%version_information numpy, matplotlib, scipy, sympy, mpmath

数值积分
我们将计算形式为
I
(
f
)
=
∫
a
b
f
(
x
)
d
x
I(f) = \int_a^b f(x) dx
I
(
f
)
=
∫
a
b
f
(
x
)
d
x
的定积分,积分的上下限分别为a和b,区间可以是有限的、半无穷的和无穷的。
积分
I
(
f
)
I(f)
I
(
f
)
可以理解为积分函数
f
(
x
)
f(x)
f
(
x
)
的曲线和x轴之间的面积。
x = np.linspace(0, 5, 100)
plt.plot(x, np.sin(x))
plt.fill_between(x[np.sin(x) > 0], 0, np.sin(x[np.sin(x) > 0]), alpha = 0.6)
plt.fill_between(x[np.sin(x) < 0], 0, np.sin(x[np.sin(x) < 0]), alpha = 0.6)
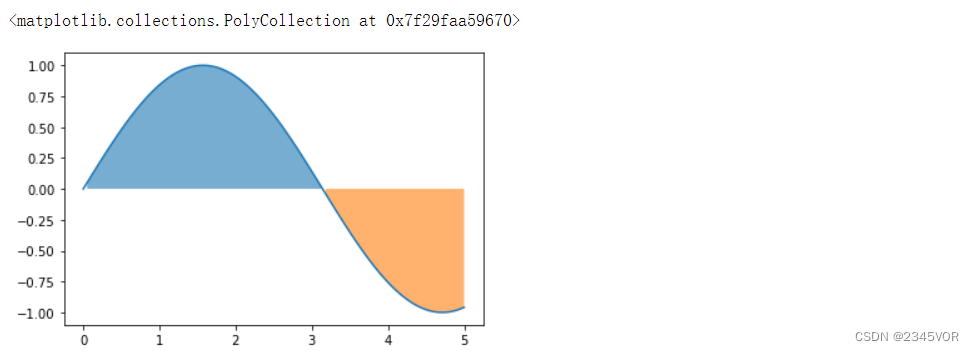
一种计算上述形式积分
I
(
f
)
I(f)
I
(
f
)
的策略是,将积分写成积分函数值的离散和:
I
(
f
)
=
∑
i
=
1
n
w
i
f
(
x
i
)
+
r
n
I(f) = \sum_{i=1}^{n} w_i f(x_i)+r_n
I
(
f
)
=
i
=
1
∑
n
w
i
f
(
x
i
)
+
r
n
其中
w
i
w_i
w
i
是函数
f
(
x
)
f(x)
f
(
x
)
在点
x
i
x_i
x
i
处的权重,
r
n
r_n
r
n
是近似误差。
I
(
f
)
I(f)
I
(
f
)
这个求和公式被称为n点求积法则,其中n的选择、点的位置、权重因子都会对计算的准确性和复杂性产生影响。
积分法则
积分法则可以通过在区间[a, b]上对函数
f
(
x
)
f(x)
f
(
x
)
进行插值推导而来。如果
x
i
x_i
x
i
在区间[a, b]上是均匀间隔的,那么可以使用多项式插值,得到的公式被称为
牛顿-科特斯求积公式
。
使用中间点的零阶多项式逼近
f
(
x
)
f(x)
f
(
x
)
,可以得到:
∫
a
b
f
(
x
)
d
x
≈
f
(
a
+
b
2
)
∫
a
b
d
x
=
(
b
−
a
)
a
+
b
2
\int_a^b f(x) dx \approx f(\frac{a+b}{2}) \int_a^b dx = (b-a)\frac{a+b}{2}
∫
a
b
f
(
x
)
d
x
≈
f
(
2
a
+
b
)
∫
a
b
d
x
=
(
b
−
a
)
2
a
+
b
这被称为中点公式。
使用一阶多项式(线性)逼近
f
(
x
)
f(x)
f
(
x
)
,可以得到:
∫
a
b
f
(
x
)
d
x
≈
b
−
a
2
(
f
(
a
)
+
f
(
b
)
)
\int_a^b f(x) dx \approx \frac{b-a}{2}(f(a)+f(b))
∫
a
b
f
(
x
)
d
x
≈
2
b
−
a
(
f
(
a
)
+
f
(
b
)
)
这被称为梯形公式公式。
辛普森求积公式 Simpson’s rule
使用二阶插值多项式,将会得到辛普森公式:
∫
a
b
f
(
x
)
d
x
≈
b
−
a
6
(
f
(
a
)
+
4
f
(
a
+
b
2
)
+
f
(
b
)
)
\int_a^b f(x) dx \approx \frac{b-a}{6}(f(a)+4f(\frac{a+b}{2})+f(b))
∫
a
b
f
(
x
)
d
x
≈
6
b
−
a
(
f
(
a
)
+
4
f
(
2
a
+
b
)
+
f
(
b
)
)
我们这里使用SymPy符号化推导该公式。
a, b, X = sympy.symbols("a, b, x")
f = sympy.Function("f")
x = a, (a+b)/2, b # simpson's rule
w = [sympy.symbols("w_%d" % i) for i in range(len(x))]
q_rule = sum([w[i] * f(x[i]) for i in range(len(x))])
q_rule

为了得到适合权重因子
w
i
w_i
w
i
的值,我们使用多项式基函数
{
ϕ
n
(
x
)
=
x
n
}
n
=
0
2
\left\{ \phi_n(x)=x^n \right\}_{n=0}^2
{
ϕ
n
(
x
)
=
x
n
}
n
=
0
2
对
f
(
x
)
f(x)
f
(
x
)
进行插值。
phi = [sympy.Lambda(X, X**n) for n in range(len(x))]
phi
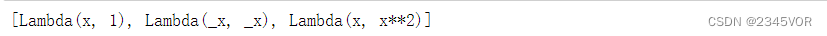
将求和公式中的
f
(
x
)
f(x)
f
(
x
)
替换为基函数
ϕ
n
(
x
)
\phi_n(x)
ϕ
n
(
x
)
,对权重因子进行解析求解:
∑
i
=
1
2
w
i
ϕ
n
(
x
i
)
=
∫
a
b
ϕ
n
(
x
)
d
x
\sum_{i=1}^{2} w_i \phi_n(x_i) = \int_a^b \phi_n(x) dx
i
=
1
∑
2
w
i
ϕ
n
(
x
i
)
=
∫
a
b
ϕ
n
(
x
)
d
x
eqs = [q_rule.subs(f, phi[n]) - sympy.integrate(phi[n](X), (X, a, b)) for n in range(len(phi))]
eqs

通过求解该线性方程组可以得到权重因子的解析表达式。
w_sol = sympy.solve(eqs, w)
w_sol
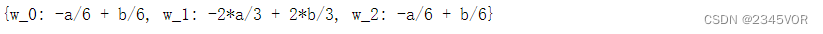
得到辛普森求积公式的解析表达式。
q_rule.subs(w_sol).simplify()

高斯求积公式 Gaussian quadrature
牛顿-科特斯求积公式的采样点在积分区间上是均匀分布的,对于非均匀分布采样,可以使用
高斯求积公式
。
我们可以把函数
f
(
x
)
f(x)
f
(
x
)
写作$ f(x) = W(x)g(x)
,
其
中
,其中
,
其
中
g(x)$是近似多项式,
W
(
x
)
W(x)
W
(
x
)
是已知的权重函数,这样我们就有
∫
−
1
1
f
(
x
)
d
x
=
∫
−
1
1
W
(
x
)
g
(
x
)
d
x
≈
∑
i
=
1
n
w
i
′
g
(
x
i
)
\int _{-1}^{1}f(x)dx=\int _{-1}^{1}W(x)g(x)dx\approx \sum _{i=1}^{n}w_{i}’g(x_{i})
∫
−
1
1
f
(
x
)
d
x
=
∫
−
1
1
W
(
x
)
g
(
x
)
d
x
≈
i
=
1
∑
n
w
i
′
g
(
x
i
)
常见的权重函数有
W
(
x
)
=
(
1
−
x
2
)
−
1
/
2
W(x)=(1-x^{2})^{-1/2}
W
(
x
)
=
(
1
−
x
2
)
−
1
/
2
(高斯切比雪夫)、
W
(
x
)
=
e
−
x
2
W(x)=e^{
{-x^{2}}}
W
(
x
)
=
e
−
x
2
(高斯埃米特)等。
权重函数
W
(
x
)
=
1
W(x)=1
W
(
x
)
=
1
时,关联多项式为勒让得多项式
P
n
(
x
)
P_{n}(x)
P
n
(
x
)
,这种方法通常称为高斯勒让德求积。
使用SciPy进行数值积分
SciPy的integrate模块中的数值求积函数可以分为两类:一类将被积函数作为Python函数传入,另一类将被积函数在给定点的样本值以数组的形式传入。第一类函数使用高斯求积法(
quad
、
quadrature
、
fixed_quad
),第二类函数使用牛顿-科斯特求积法(
trapezoid
、
simpson
、
romb
)。
高斯积分
quadrature
函数是一个使用Python实现的自适应高斯求积程序。
quadrature
函数会重复调用
fixed_quad
函数,并不断增加多项式的次数,直到满足所需的精度。
quad
函数是对Fortran库QUADPACK的封装,有更好的性能。一般情况下优先使用
quad
函数。
考虑定积分
∫
−
1
1
e
−
x
2
d
x
\int _{-1}^{1}e^{-x^2}dx
∫
−
1
1
e
−
x
2
d
x
def f(x):
return np.exp(-x**2)
val, err = integrate.quad(f, -1, 1)
val, err

quad
函数返回一个元组,包含积分的数值结果和绝对误差估计。可以使用参数epsabs和epsrel来设置绝对误差和相对误差的容忍度。
quad
函数的关键词参数args可以将函数的参数值传递给被积函数。
考虑含参数定积分
∫
−
1
1
a
e
−
(
x
−
b
)
2
/
c
2
d
x
\int _{-1}^{1}ae^{-(x-b)^2/c^2}dx
∫
−
1
1
a
e
−
(
x
−
b
)
2
/
c
2
d
x
def f(x, a, b, c):
return a * np.exp(-((x-b)/c)**2)
val, err = integrate.quad(f, -1, 1, args=(1, 2, 3))
val, err
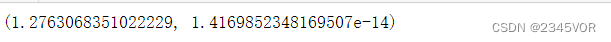
当被积分函数的变量不是第一个参数是,可以使用lambda函数来调整参数的顺序。
例如我们使用
scipy.special
模块的jv函数计算0阶贝塞尔函数的积分,jv函数的第一个参数是贝塞尔函数的阶数,第二个参数是变量x。
from scipy.special import jv
val, err = integrate.quad(lambda x: jv(0, x), 0, 5)
val, err

无穷积分
quad
函数支持无穷积分。浮点数中的无穷表达式可以使用
np.inf
获得。
考虑使用
quad
函数计算
∫
−
∞
∞
e
−
x
2
d
x
\int _{-\infty}^{\infty}e^{-x^2}dx
∫
−
∞
∞
e
−
x
2
d
x
f = lambda x: np.exp(-x**2)
val, err = integrate.quad(f, -np.inf, np.inf)
val, err
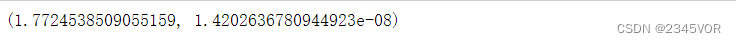
发散函数积分
通过一些额外信息,
quad
函数也可以处理带可积奇点的函数。
考虑积分
∫
−
1
1
1
∣
x
∣
d
x
\int _{-1}^{1} \frac{1}{\sqrt{|x|}}dx
∫
−
1
1
∣
x
∣
1
d
x
,被积函数在
x
=
0
x=0
x
=
0
处是发散的。
f = lambda x: 1/np.sqrt(abs(x))
fig, ax = plt.subplots(figsize=(8, 3))
a, b = -1, 1
x = np.linspace(a, b, 10000)
ax.plot(x, f(x), lw=2)
ax.fill_between(x, f(x), color='green', alpha=0.5)
ax.set_xlabel("$x$", fontsize=18)
ax.set_ylabel("$f(x)$", fontsize=18)
ax.set_ylim(0, 25)
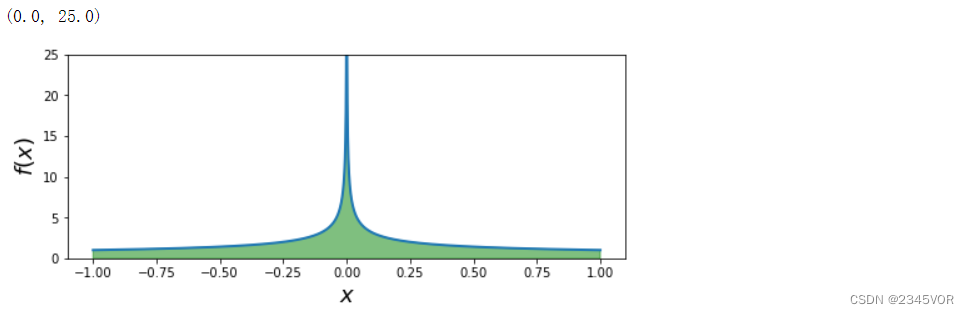
integrate.quad(f, a, b) # 直接使用quad函数求积分,可能会失败

integrate.quad(f, a, b, points=[0])
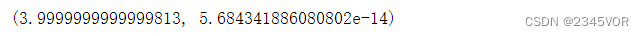
quad
函数的points参数可以设置需要绕过的点,从而正确地计算积分。
列表积分
quad
函数只适合于被积函数可以被Python函数表示的积分。如果被积函数来自实验或者观察数据,其可能只可以在某些预先确定的点求值。这种情况下,可以使用牛顿-科特斯求积法,如之前介绍的中间点公式、梯形公式或辛普森公式。
在SciPy的integrate模块中,
trapezoid
和
simpson
函数分别实现了复化梯形公式和辛普森公式。这些函数的第一个参数是数组y,第二个参数是采样点数组x或者采样点间隔dx。
考虑积分
∫
0
2
x
d
x
\int _{0}^{2} \sqrt{x} dx
∫
0
2
x
d
x
,积分区间为[0, 2],采样点数目25。
f = lambda x: np.sqrt(x)
a, b = 0, 2
x = np.linspace(a, b, 25)
y = f(x)
fig, ax = plt.subplots(figsize=(8, 3))
ax.plot(x, y, 'bo')
xx = np.linspace(a, b, 500)
ax.plot(xx, f(xx), 'b-')
ax.fill_between(xx, f(xx), color='green', alpha=0.5)
ax.set_xlabel(r"$x$", fontsize=18)
ax.set_ylabel(r"$f(x)$", fontsize=18)
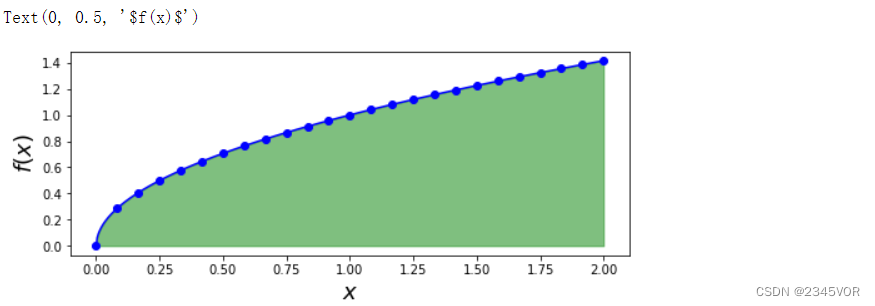
通过解析积分可以得到积分的精确值。
val_exact = 2.0/3.0 * (b-a)**(3.0/2.0)
val_exact

要计算这个积分,将数组y和x传递给trapezoid函数或simpson函数。
val_trapz = integrate.trapz(y, x)
val_trapz - val_exact

val_simps = integrate.simps(y, x)
val_simps - val_exact

trapezoid
函数和
simpson
函数无法提供对误差的估计。提供准确度的方法是增加样品点的数量或者使用更高阶的方法。
integrate模块中的
romb
函数实现了
Romberg方法
。这种方法使用均匀间隔的采样点(数目为
2
n
+
1
2^n+1
2
n
+
1
),同时使用Richardson外推算法来加速梯形法的收敛。
x = np.linspace(a, b, 1 + 2**6)
y = f(x)
val_romb = integrate.romb(y, dx=(x[1]-x[0]))
val_romb - val_exact
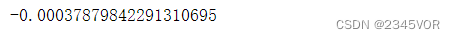
一般情况下,推荐使用simpson函数。
多重积分
多重积分,例如二重积分
∫
a
b
∫
c
d
f
(
x
,
y
)
d
x
d
y
\int _{a}^{b}\int _{c}^{d}f(x, y)dxdy
∫
a
b
∫
c
d
f
(
x
,
y
)
d
x
d
y
和三重积分
∫
a
b
∫
c
d
∫
e
f
f
(
x
,
y
,
z
)
d
x
d
y
d
z
\int _{a}^{b}\int _{c}^{d}\int _{e}^{f}f(x, y, z)dxdydz
∫
a
b
∫
c
d
∫
e
f
f
(
x
,
y
,
z
)
d
x
d
y
d
z
,可以使用SciPy的integrate模块的
dblquad
和
tplquad
函数。n个变量的积分也可以使用
nquad
函数来计算。这些函数都是对单变量求积函数
quad
的封装,沿着被积函数每个维度重复调用quad函数。
考虑二重积分
∫
0
1
∫
0
1
e
−
x
2
−
y
2
d
x
d
y
\int _{0}^{1}\int _{0}^{1}e^{-x^2-y^2}dxdy
∫
0
1
∫
0
1
e
−
x
2
−
y
2
d
x
d
y
def f(x, y):
return np.exp(-x**2-y**2)
fig, ax = plt.subplots(figsize=(6, 5))
x = y = np.linspace(-1.25, 1.25, 75)
X, Y = np.meshgrid(x, y)
c = ax.contour(X, Y, f(X, Y), 15, cmap=mpl.cm.RdBu, vmin=-1, vmax=1)
bound_rect = plt.Rectangle((0, 0), 1, 1,
facecolor="grey")
ax.add_patch(bound_rect)
ax.axis('tight')
ax.set_xlabel('$x$', fontsize=18)
ax.set_ylabel('$y$', fontsize=18)
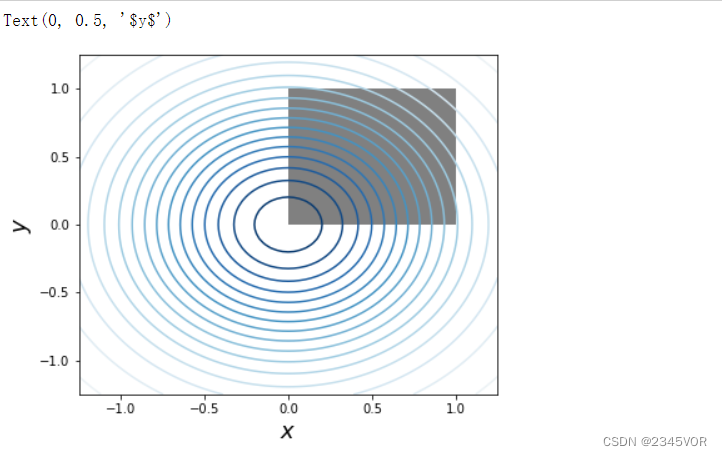
本例中,x和y的积分限都是固定的。
dblquad
函数要求y变量的积分限用变量为x的函数表示,因此我们需要定义两个函数
g
(
x
)
g(x)
g
(
x
)
和
h
(
x
)
h(x)
h
(
x
)
,二者返回常量。
a, b = 0, 1
g = lambda x: 0
h = lambda x: 1
val, err = integrate.dblquad(f, a, b, g, h) # 参数g和h为函数
val, err

对于形如
∫
0
1
∫
0
1
∫
0
1
e
−
x
2
−
y
2
−
z
2
d
x
d
y
d
z
\int _{0}^{1}\int _{0}^{1}\int _{0}^{1}e^{-x^2-y^2-z^2}dxdydz
∫
0
1
∫
0
1
∫
0
1
e
−
x
2
−
y
2
−
z
2
d
x
d
y
d
z
的三重积分,可以使用
nquad
函数计算。除了继续使用
g
(
x
)
g(x)
g
(
x
)
和
h
(
x
)
h(x)
h
(
x
)
表示y轴的积分限之外,我们需要额外提供两个函数
q
(
x
,
y
)
q(x, y)
q
(
x
,
y
)
和
r
(
x
,
y
)
r(x, y)
r
(
x
,
y
)
表示z轴的积分限。注意这里使用了x和y两个坐标。
def f(x, y, z):
return np.exp(-x**2-y**2-z**2)
val, err = integrate.tplquad(f, 0, 1, lambda x : 0, lambda x : 1, lambda x, y : 0, lambda x, y : 1)
val, err
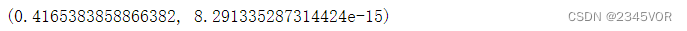
对于任意维度数目的积分,可以使用
nquad
函数。它的第二个参数是用于指定积分限的列表,列表里面包含每个积分变量的积分限元组,或者包含能够返回积分限的函数。
integrate.nquad(f, [(0, 1), (0, 1), (0, 1)]) # 元素相同的列表可以使用 [(0, 1)] * 3 生成
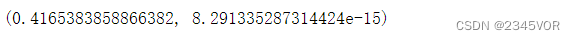
维数灾难
在数值积分中,多重积分的计算复杂度和维数成指数关系。
def f(*args):
return np.exp(-np.sum(np.array(args)**2))
for dim in range(1, 5):
print(dim)
%time integrate.nquad(f, [(0,1)] * dim)

随着维数增加,高维积分的直接求积方法变得不切实际。如果对计算精度要求不是非常高,可以使用蒙特卡罗积分。蒙特卡罗积分在维度上的扩展性非常好,对于高维积分是一种有效的工具。
符号积分和任意精度积分
在符号计算的章节,我们已经演示了使用SymPy的sympy.integrate函数来计算符号函数的有限积分和无限积分。
例如,计算积分
∫
−
1
1
2
1
−
x
2
d
x
\int_{-1}^{1} 2 \sqrt{1-x^2} dx
∫
−
1
1
2
1
−
x
2
d
x
x = sympy.symbols("x")
f = 2 * sympy.sqrt(1-x**2)
a, b = -1, 1
sympy.plot(f, (x, -2, 2))
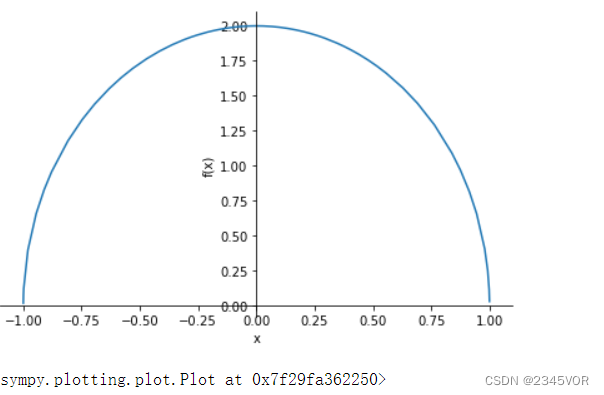
val_sym = sympy.integrate(f, (x, a, b))
val_sym

存在精确解析解的问题是一种特例。数值方法的精度受算法和浮点精度制约。mpmath库为任意精度计算提供了数值方法。为了按照给定的精度计算积分,可以使用
mpmath.quad
函数。为了设置精度,我们把变量mpmath.mp.dps设置为所需精度的小数位数。
mpmath.mp.dps = 75 # 75位小数的精度
被积分的Python函数可以使用mpmath库中的数学函数。可以使用
sympy.lambdify
从一个SymPy表达式中创建这样的函数。
f_mpmath = sympy.lambdify(x, f, 'mpmath')
val = mpmath.quad(f_mpmath, (a, b))
val # 返回的对象类型是高精度浮点数
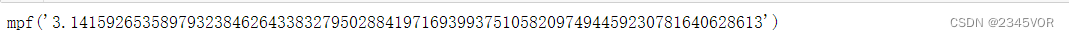
sympy.sympify(val)

我们可以将这个结果与解析结果进行对比。
sympy.N(val_sym, mpmath.mp.dps+1) - val
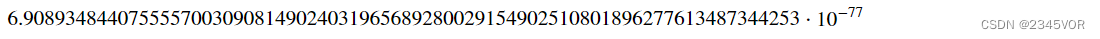
SciPy的integrate模块中的quad函数无法达到这样的精度,因为受浮点数精度的限制。
多重积分
mpmath库中的
quad
函数也可以用于计算多重积分。计算这样的积分,只需要把拥有多个变量参数的被积函数传给
quad
函数,并未每个积分变量传入积分限的元组。
计算下面的双重积分
∫
0
1
∫
0
1
cos
(
x
)
cos
(
y
)
e
−
x
2
−
y
2
d
x
\int_{0}^{1} \int_{0}^{1} \cos(x) \cos(y) e^{-x^2-y^2} dx
∫
0
1
∫
0
1
cos
(
x
)
cos
(
y
)
e
−
x
2
−
y
2
d
x
def f2(x, y):
return np.cos(x)*np.cos(y)*np.exp(-x**2-y**2)
integrate.dblquad(f2, 0, 1, lambda x : 0, lambda x : 1)

x, y, z = sympy.symbols("x, y, z")
f2 = sympy.cos(x)*sympy.cos(y)*sympy.exp(-x**2-y**2)
f2_mpmath = sympy.lambdify((x, y), f2, 'mpmath')
mpmath.mp.dps = 30 # 指定计算精度
res = mpmath.quad(f2_mpmath, (0, 1), (0, 1))
res

由于高精度浮点运算是在CPU上模拟实现的,缺点是非常慢。
曲线积分
SymPy可以使用line_integral函数来计算形如
∫
C
f
(
x
,
y
)
d
s
\int_{C} f(x, y) ds
∫
C
f
(
x
,
y
)
d
s
的曲线积分,其中C是x-y平面上的曲线。该函数的第一个参数是SymPy表示的被积函数,第二个参数是一个sympy.Curve实例,第三个参数是积分变量的列表。
例如,创建Curve实例来表示单位圆的路径。
t, x, y = sympy.symbols("t, x, y")
C = sympy.Curve([sympy.cos(t), sympy.sin(t)], (t, 0, 2 * sympy.pi))
积分路径指定之后,我们对被积函数
f
(
x
,
y
)
=
1
f(x, y)=1
f
(
x
,
y
)
=
1
进行积分,积分结果就是圆的周长。
sympy.line_integrate(1, C, [x, y])

积分变换
积分变换是将一个函数作为输入,然后输出另有一个函数的过程。这里我们介绍使用SymPy支持的两种积分变换,
拉普拉斯变换
和
傅里叶变换
。这两种变换有很多应用,例如可以使用拉普拉斯变换将微分方程转换为代数方程,或者使用傅里叶变换将时域问题转换为频域问题。
一般来说,函数
f
(
t
)
f(t)
f
(
t
)
的积分变换可以写为:
T
f
(
u
)
=
∫
t
1
t
2
K
(
t
,
u
)
f
(
t
)
d
t
T_f(u) = \int_{t_1}^{t_2} K(t, u) f(t) dt
T
f
(
u
)
=
∫
t
1
t
2
K
(
t
,
u
)
f
(
t
)
d
t
其中
T
f
(
u
)
T_f(u)
T
f
(
u
)
是变换后的函数,
K
(
t
,
u
)
K(t, u)
K
(
t
,
u
)
是变换的核函数。
积分变换的逆变换是:
f
(
t
)
=
∫
u
1
u
2
K
−
1
(
t
,
u
)
T
f
(
u
)
d
u
f(t) = \int_{u_1}^{u_2} K^{-1}(t, u) T_f(u) du
f
(
t
)
=
∫
u
1
u
2
K
−
1
(
t
,
u
)
T
f
(
u
)
d
u
其中
K
−
1
(
t
,
u
)
K^{-1}(t, u)
K
−
1
(
t
,
u
)
是核函数的逆变换。
拉普拉斯变换
F
(
s
)
=
∫
0
∞
f
(
t
)
e
−
s
t
d
t
F(s)=\int _{0}^{\infty }f(t)e^{-st}\,\mathrm {d} t
F
(
s
)
=
∫
0
∞
f
(
t
)
e
−
s
t
d
t
及其逆变换
f
(
t
)
=
L
−
1
{
F
}
(
t
)
=
1
2
π
i
lim
T
→
∞
∫
γ
−
i
T
γ
+
i
T
e
s
t
F
(
s
)
d
s
f(t)={\mathcal {L}}^{-1}\{F\}(t)={\frac {1}{2\pi i}}\lim _{T\to \infty }\int _{\gamma -iT}^{\gamma +iT}e^{st}F(s)\,\mathrm {d} s
f
(
t
)
=
L
−
1
{
F
}
(
t
)
=
2
π
i
1
T
→
∞
lim
∫
γ
−
i
T
γ
+
i
T
e
s
t
F
(
s
)
d
s
以及傅里叶变换
f
^
(
ξ
)
=
∫
−
∞
∞
f
(
x
)
e
−
2
π
i
x
ξ
d
x
\hat{f}(\xi) = \int_{-\infty}^\infty f(x)\ e^{- 2\pi i x \xi}\,dx
f
^
(
ξ
)
=
∫
−
∞
∞
f
(
x
)
e
−
2
π
i
x
ξ
d
x
及其逆变换
f
(
x
)
=
∫
−
∞
∞
f
^
(
ξ
)
e
2
π
i
ξ
x
d
ξ
f(x) = \int_{-\infty}^\infty \hat f(\xi)\ e^{2 \pi i \xi x}\,d\xi
f
(
x
)
=
∫
−
∞
∞
f
^
(
ξ
)
e
2
π
i
ξ
x
d
ξ
在SymPy中,拉普拉斯变换和傅里叶变换对应的函数为
sympy.laplace_transform
和
sympy.fourier_transform
,其逆变换为
sympy.inverse_laplace_transform
和
sympy.inverse_fourier_transform
。
示例
计算函数
f
(
t
)
=
sin
(
a
t
)
f(t) = \sin(at)
f
(
t
)
=
sin
(
a
t
)
的拉普拉斯变换
s = sympy.symbols("s")
a, t = sympy.symbols("a, t", positive=True)
f = sympy.sin(a*t)
sympy.laplace_transform(f, t, s)

默认情况下,
laplace_transform
函数返回一个元组,包含转换结果和变换的收敛条件。如果只需要转换结果,可以使用参数noconds=True去除返回中的条件。
F = sympy.laplace_transform(f, t, s, noconds=True)
F

逆变换将得到原始函数:
sympy.inverse_laplace_transform(F, s, t, noconds=True)

我们将在微分方程章节中拉普拉斯变换的应用。
示例
计算函数
f
(
t
)
=
e
−
a
t
2
f(t) = e^{-at^2}
f
(
t
)
=
e
−
a
t
2
的傅里叶变换
w = sympy.symbols("omega")
a, t = sympy.symbols("a, t", positive=True)
f = sympy.exp(-a*t**2)
F = sympy.fourier_transform(f, t, w)
F

sympy.inverse_fourier_transform(F, w, t)

我们在将在信号处理章节中演示傅里叶变换在降噪中的应用。
参考文献来自桑鸿乾老师的课件:
科学计算和人工智能