博客

【C++从入门到踹门】第十九篇：bitset（位图）的使用与实现

  • Post author:
  • Post category:其他


目录

在这里插入图片描述



概念引入

给40亿个不重复的无符号整数，且为乱序，给一个无符号整数，如何快速判断一个数是否在这40亿个数中？

常规的想法是将40亿个数存入数组中，快速排序然后采用二分法查找，时间复杂度O(NlogN).或者是将一堆数存入unordered_set容器中，使用find进行查找，时间复杂度为O(N)。

但是内存空间存不下这么多的数字：

40亿≈2

32=2

2 * 2^10 * 2^10 * 2^10=4 * 1024 * 1024 * 1024 = 4G

每个整数占4字节，所以40亿个整数占用16G字节的空间

而一台32位机的内存地址有32位，每个地址指向1字节（8bits）的数据，其内存地址空间的大小只有2^32=4G字节的空间大小，由于系统本身要占据一部分内存，我们可用的内存只有3.2G左右。

如果我们直接按整型的方式40亿个整数存入内存显然是不可能的事。

于是我们需要使用位图（bitset）来解决：

这个问题只需要考虑数字在或者不在，那么我们仅需要0，1来表示其存在性（0表示不在，1表示存在），而使用二进制比特位来标记该数字的位置：

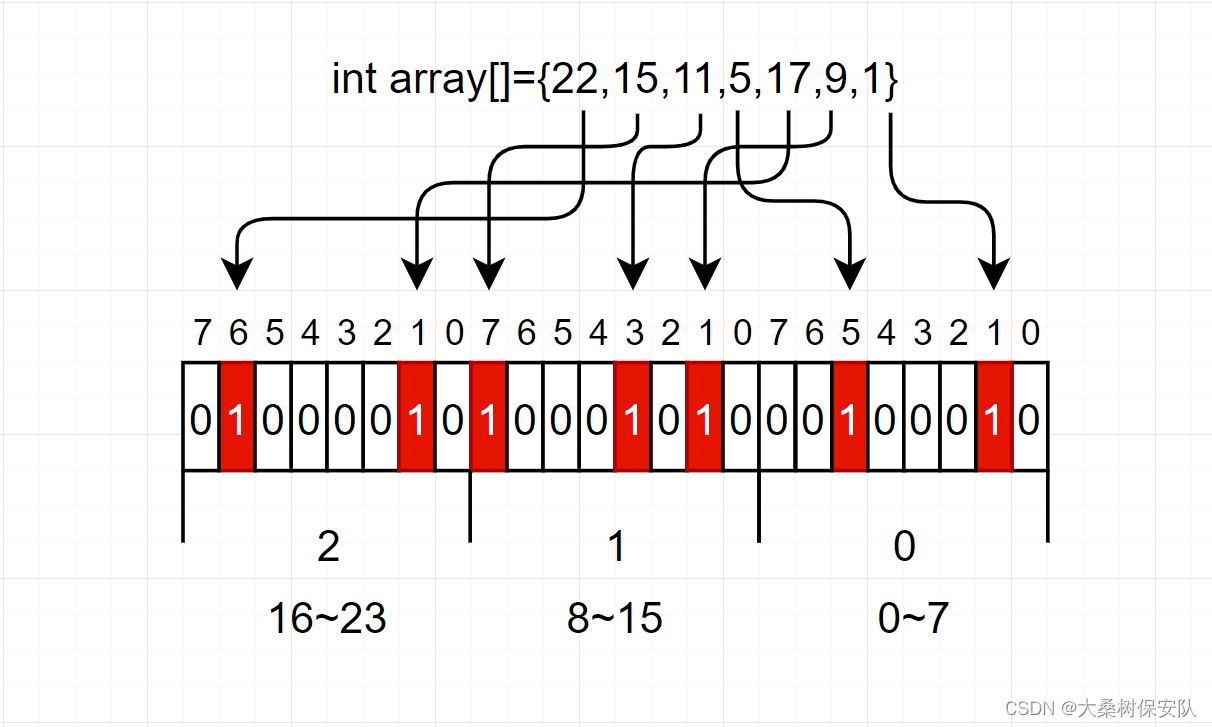
在这里插入图片描述

那么每个数的是否存在仅用一个bit位就能表示了。

40亿个数的状态占用2^32个bit=4 * 1024 * 1024 * 1024 bit=0.5G ，显然内存占用变小了很多。


所谓位图，就是用比特位来存放数据的状态，适用于海量数据，数据无重复的场景，通常用于判断数据存不存在。



bitset类

标准库提供了位图：

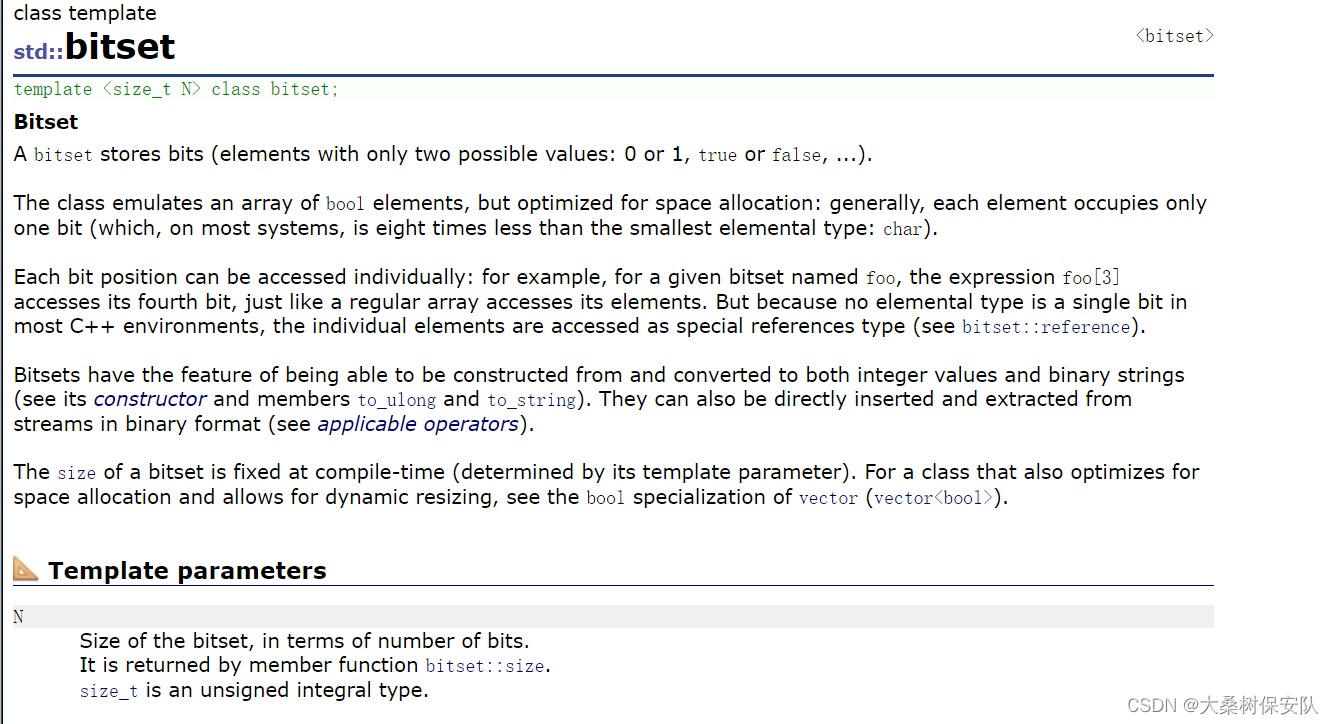
在这里插入图片描述

该类模拟了bool类型元素的数组，但是每个元素只占用一个bit位，一个char可以存放8个元素。

每一个位的位置可以单独访问，例如一个bitset对象foo，可以类似于数组使用下标访问的方式：foo[ 3 ],来访问第四个元素。

模板参数N表示元素的数量。



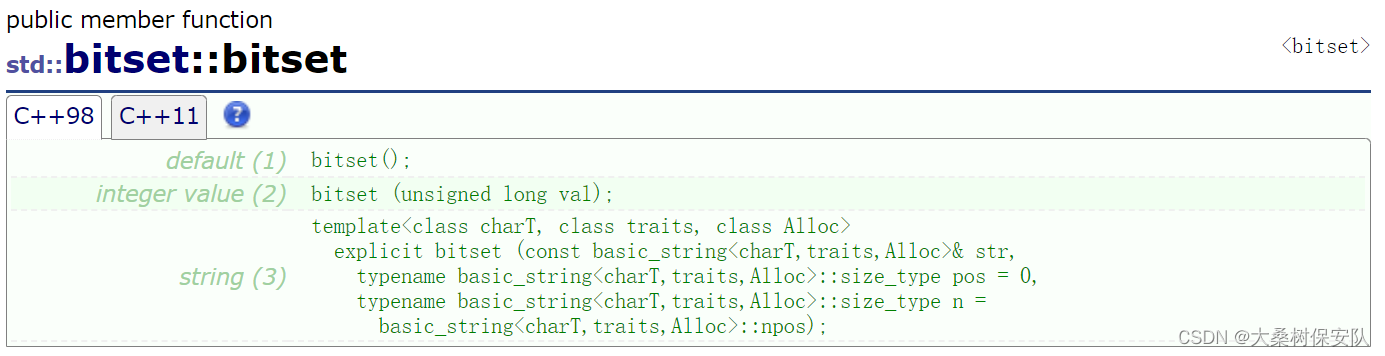
bitset的构造

在这里插入图片描述

  • （1）默认构造函数

    所有元素都初始化为0

  • （2）使用整型初始化

    元素按照给定整数的二进制位进行初始化：0xff ——> 1111 1111

  • （3）字符串初始化

    使用01的string进行初始化：std::string(“01101001”) ——> 01101001

    使用01的字符串进行初始化：(“01101001”) ——> 01101001


  • 案例

    ： 

#include <iostream>       // std::cout
#include <string>         // std::string
#include <bitset>         // std::bitset

int main ()
{
  std::bitset<16> foo;
  std::bitset<16> bar (0xfa2);
  std::bitset<16> baz (std::string("01101001"));
  std::bitset<16> baz2("01101001");

  std::cout << "foo: " << foo << '\n';
  std::cout << "bar: " << bar << '\n';
  std::cout << "baz: " << baz << '\n';
  std::cout << "baz2: " << baz2 << '\n';

  return 0;
}

在这里插入图片描述



下标访问 operator[]

在这里插入图片描述

返回pos位的元素值或者引用，但是不执行范围检查，建议使用bitset::test ,其会检查边界。


  • 案例

    ： 
int main ()
{
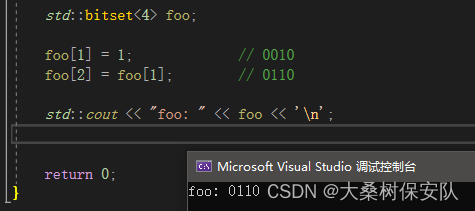
  std::bitset<4> foo;

  foo[1]=1;             // 0010
  foo[2]=foo[1];        // 0110

  std::cout << "foo: " << foo << '\n';

  return 0;
}

在这里插入图片描述



返回bit位值 test

在这里插入图片描述 

int main()
{
	std::bitset<5> foo(std::string("01011"));

	std::cout << "foo contains:\n";
	
	//运行下面的语句，将bool值从0，1转化为false，true
	std::cout << std::boolalpha;
	
	for (std::size_t i = 0; i < foo.size(); ++i)
		std::cout << foo.test(i) << '\n';
}

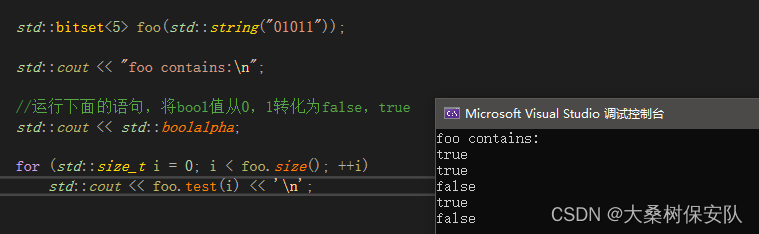
在这里插入图片描述

当使用boolalpha后，以后的bool类型结果都将以true或false形式输出，除非使用noboolalpha取消 boolalpha流的格式标志。



设置比特位 set

  • （1）把所有比特位都设置为1

  • （2）把pos处的比特位设置为1（默认true），或者第二个参数给为0（或者false），则可将pos位置为0.


  • 案例

    ： 

int main()
{
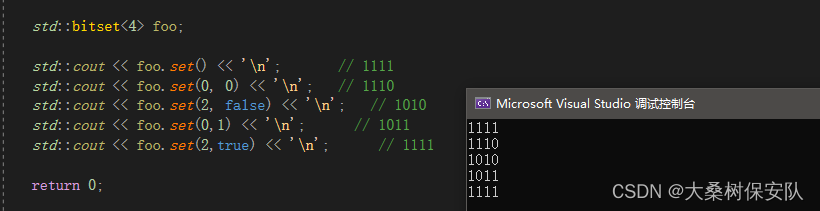
    std::bitset<4> foo;
	std::cout << foo.set() << '\n';       // 1111
	std::cout << foo.set(0, 0) << '\n';   // 1110
	std::cout << foo.set(2, false) << '\n';   // 1010
	std::cout << foo.set(0,1) << '\n';      // 1011
	std::cout << foo.set(2,true) << '\n';      // 1111

	return 0;
}

在这里插入图片描述



重置比特位 reset

在这里插入图片描述

  • （1）将所有bits重置为0

  • （2）pos位置为0


  • 案例
     

int main()
{
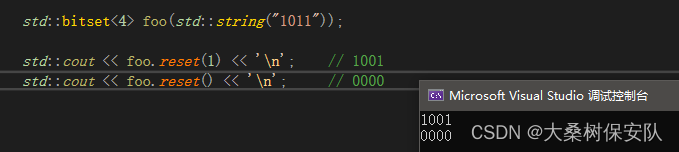
    std::bitset<4> foo(std::string("1011"));

	std::cout << foo.reset(1) << '\n';    // 1001
	std::cout << foo.reset() << '\n';     // 0000
	
	return 0;
}

在这里插入图片描述



计算元素数量 size/count

在这里插入图片描述

size返回元素的总数量，即模板参数中我们给的N。

count 返回元素中被set的元素数量。


  • 案例

    ： 
int main()
{
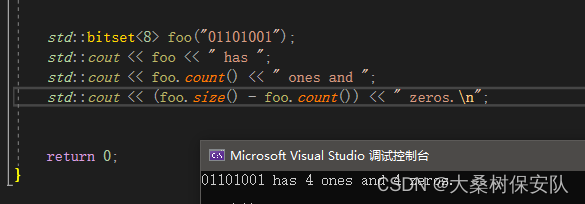
    std::bitset<8> foo("01101001");
	std::cout << foo << " has ";
	std::cout << foo.count() << " ones and ";
	std::cout << (foo.size() - foo.count()) << " zeros.\n";
	return 0;
}

在这里插入图片描述



翻转位 flip

在这里插入图片描述

  • （1）翻转所有位
  • （2）翻转pos位 
int main ()
{
  std::bitset<4> foo (std::string("0001"));

  std::cout << foo.flip(2) << '\n';     // 0101
  std::cout << foo.flip() << '\n';      // 1010

  return 0;
}



测试bitset对象中是否已有bite位被set —— any，none,all

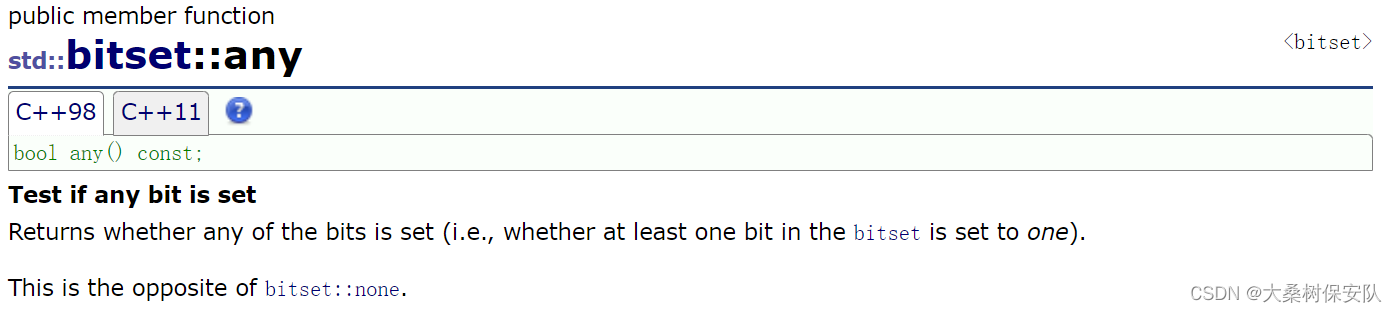
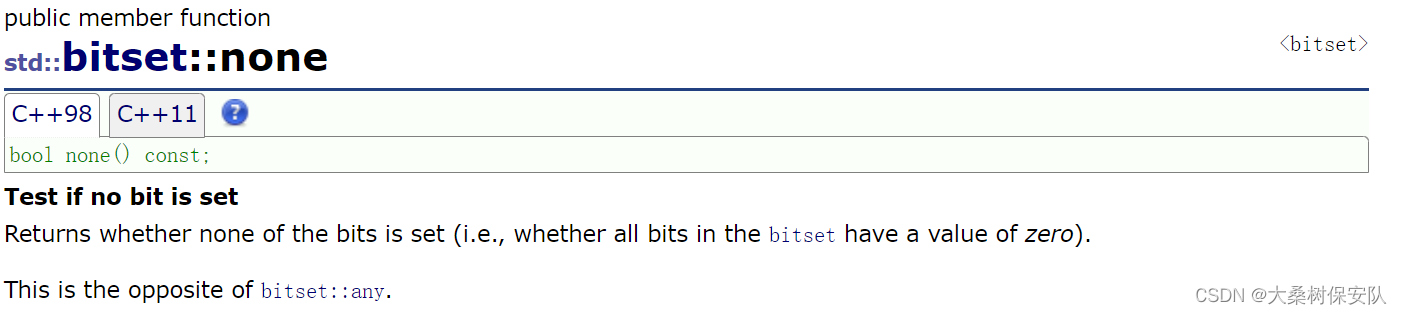
在这里插入图片描述

在这里插入图片描述

如果至少有一个bit位已设置，any返回true，否则none返回真.如果所有bit位都已set，则all返回true。 

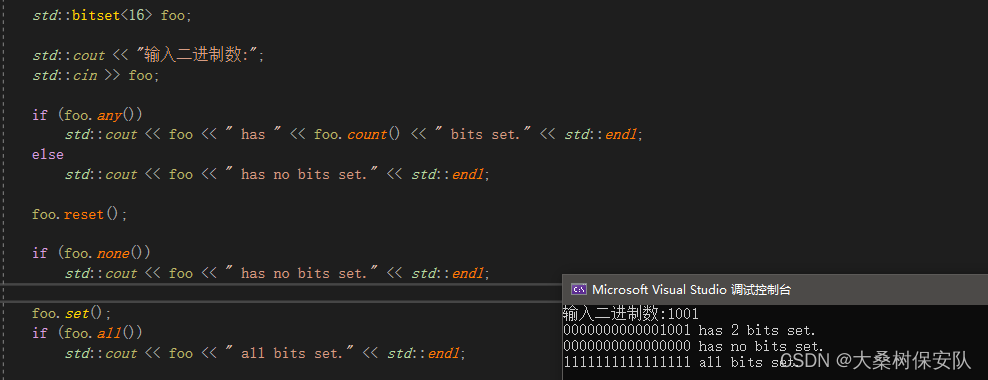
int main()
{
    std::bitset<16> foo;

	std::cout << "输入二进制数:";
	std::cin >> foo;

	if (foo.any())
		std::cout << foo << " has " << foo.count() << " bits set." << std::endl;
	else
		std::cout << foo << " has no bits set." << std::endl;

	foo.reset();

	if (foo.none())
		std::cout << foo << " has no bits set." << std::endl;

    foo.set();
    if(foo.all())
        std::cout << foo << " all bits set." << std::endl;

	return 0;
}

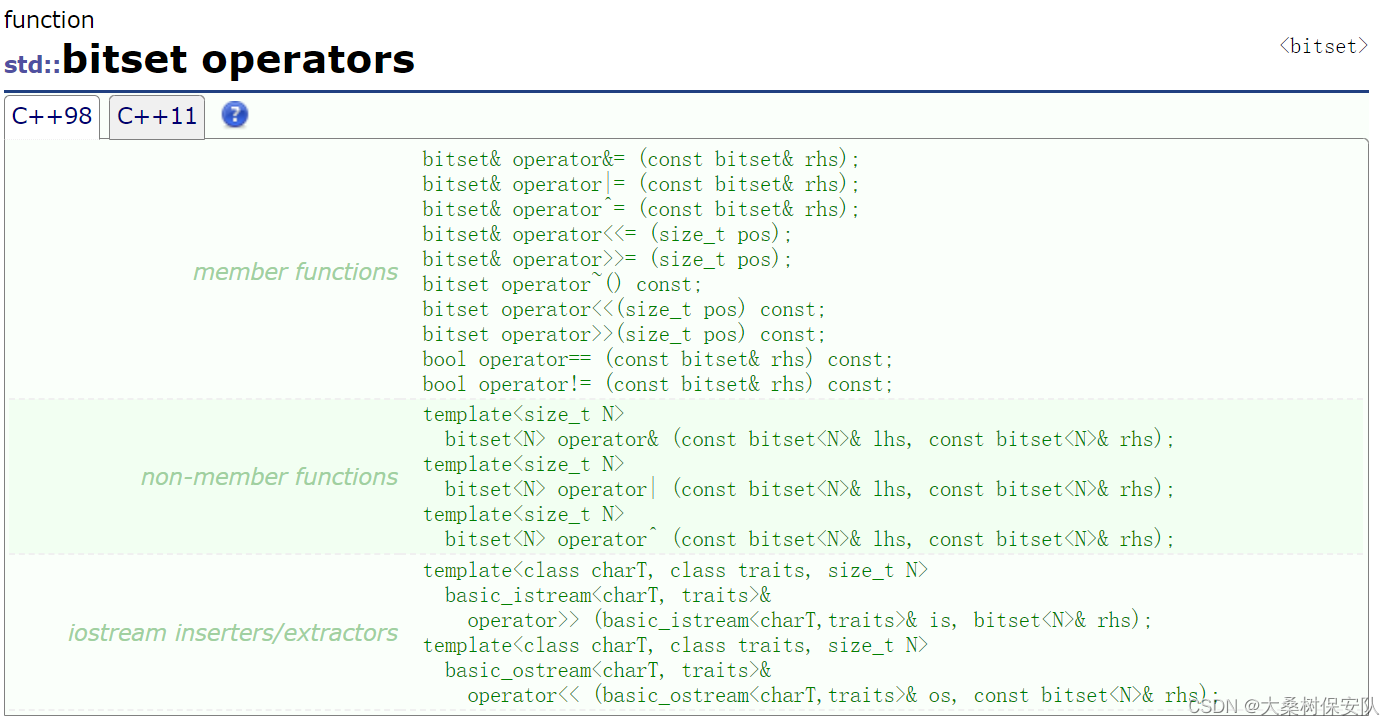
在这里插入图片描述



bitset的运算符重载

在这里插入图片描述 

int main ()
{
  std::bitset<4> foo (std::string("1001"));
  std::bitset<4> bar (std::string("0011"));

  std::cout << (foo^=bar) << '\n';       // 1010 (XOR,assign)
  std::cout << (foo&=bar) << '\n';       // 0010 (AND,assign)
  std::cout << (foo|=bar) << '\n';       // 0011 (OR,assign)

  std::cout << (foo<<=2) << '\n';        // 1100 (SHL,assign)
  std::cout << (foo>>=1) << '\n';        // 0110 (SHR,assign)

  std::cout << (~bar) << '\n';           // 1100 (NOT)
  std::cout << (bar<<1) << '\n';         // 0110 (SHL)
  std::cout << (bar>>1) << '\n';         // 0001 (SHR)

  std::cout << (foo==bar) << '\n';       // false (0110==0011)
  std::cout << (foo!=bar) << '\n';       // true  (0110!=0011)

  std::cout << (foo&bar) << '\n';        // 0010
  std::cout << (foo|bar) << '\n';        // 0111
  std::cout << (foo^bar) << '\n';        // 0101

  return 0;
}



自己实现一个bitset

如果我们以一个整型作为比特位的容器，那么如果要求0~N范围的比特位，就需要有

N/32+1

个整型来容纳这些比特位，同理如果以char为容器，则需要

N/8+1

个char来容纳N个比特位。这里我们用char数组作为底层容纳比特位的容器。 

namespace mystd 
{
	template<size_t NUM>
	class bitset
	{
	public:

		bitset()
		{
			_bits.resize(NUM/8+1, 0);
		}

		void set(size_t pos)//设置指定位或者所有位
		{}

		void reset(size_t pos)//清空指定位或者所有位
		{}

		bool test(size_t pos)//获取指定位状态
		{}

        void flip(size_t pos)//翻转指定pos
        {}

        size_t count()//统计set的位数
        {}

        bool none()//没有bit为被set返回true
        {}

        bool any()//至少一个bit位set返回true
        {}

        bool all()//全部NUM个bit位被set返回true
        {}

	private:
		vector<char> _bits;//位图
	};
}



set reset test flip

  • set是将pos位的0置为1。

首先通过 i=pos/8 找到bit位在第i个char中，再通过 j=pos%8 找到在这个char的第j位bit位上。将1左移j位后于这个char

按位或运算

即可。

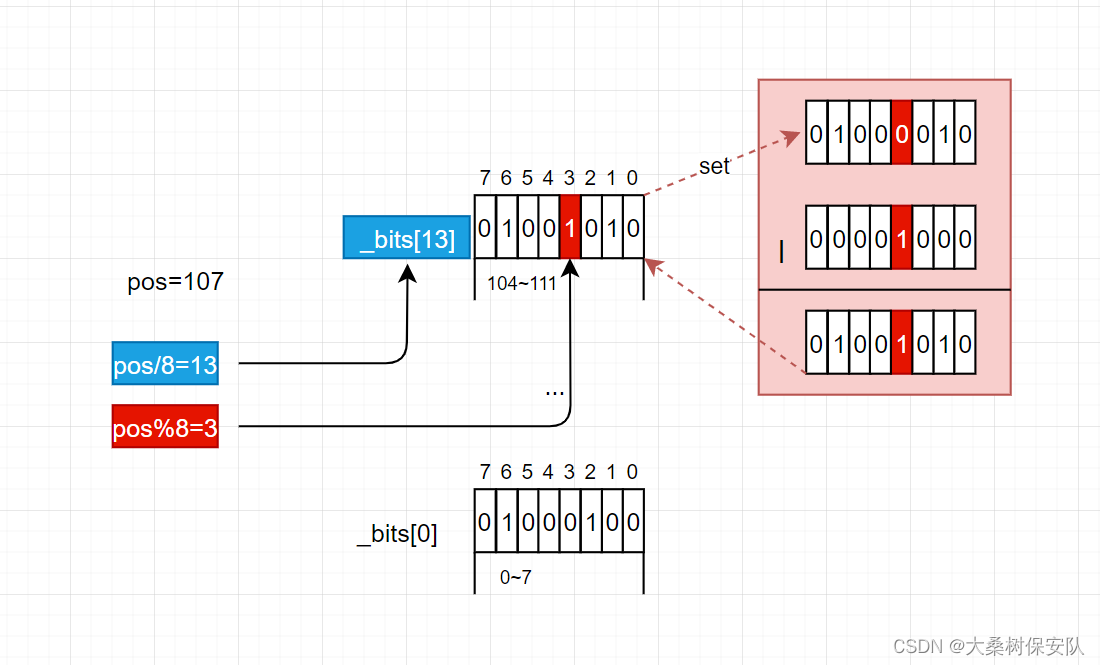
在这里插入图片描述 

void set(size_t pos)//设置指定位或者所有位
{
    size_t i = pos / 8;
    size_t j = pos % 8;

    _bits[i] |= (1 << j);
}
  • reset 将pos置0也是同理，将1左移j位，按位取反，再和这个char

    按位与运算

    即可：

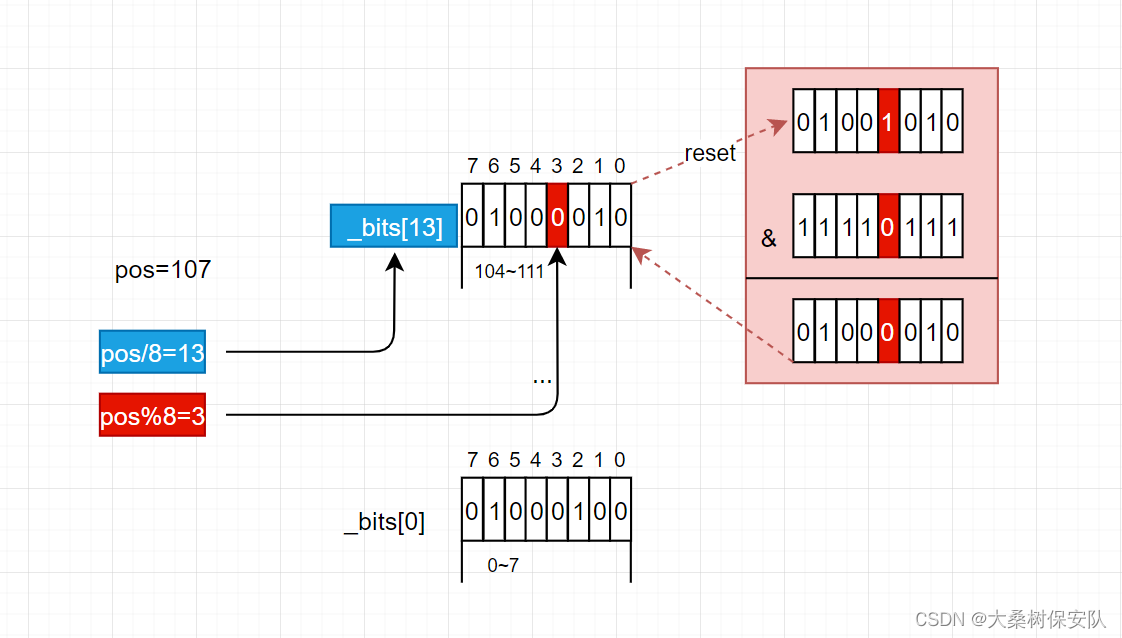
在这里插入图片描述 

void reset(size_t pos)//清空指定位或者所有位
{
    size_t i = pos / 8;
    size_t j = pos % 8;
    
    _bits[i] &= (~(1 << j));
}
  • test获取位的状态，将1左移j位，再和这个char

    按位与运算

    即可：

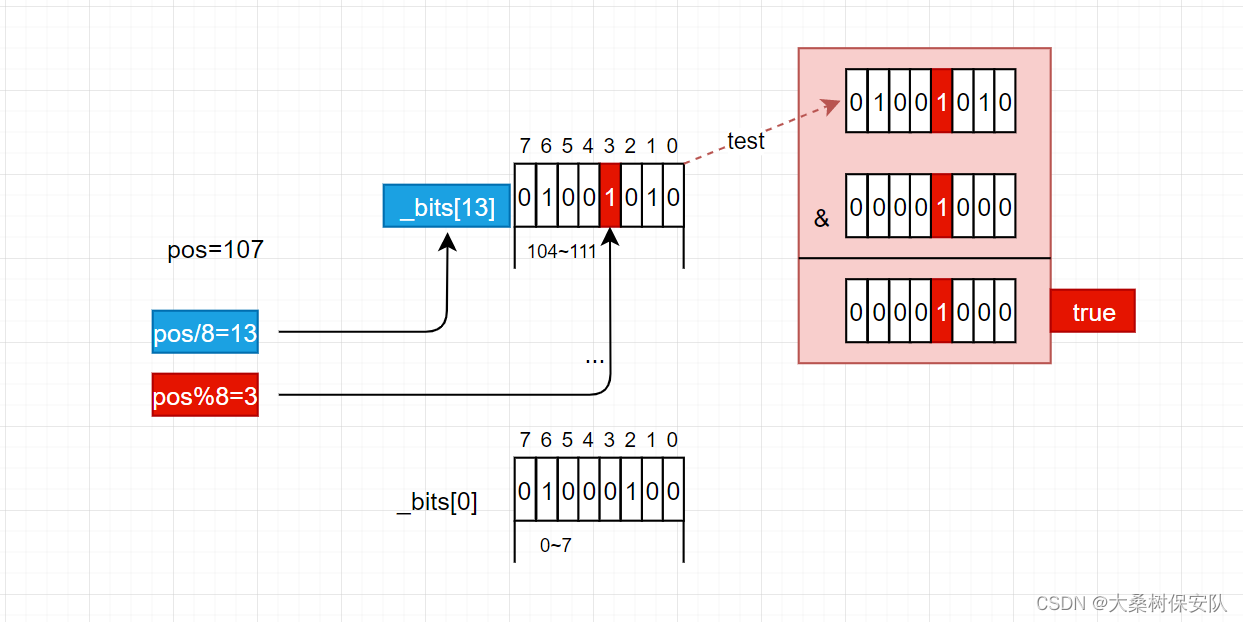
在这里插入图片描述 

bool test(size_t pos)//获取指定位状态
{
    size_t i = pos / 8;
    size_t j = pos % 8;

    return _bits[i] & (1 << j);
}
  • flip翻转位
  1. 计算出该位位于第 i 个char的第 j 个比特位。
  2. 将1左移 j 位后与第 i 个char进行

    按位异或运算

    即可。

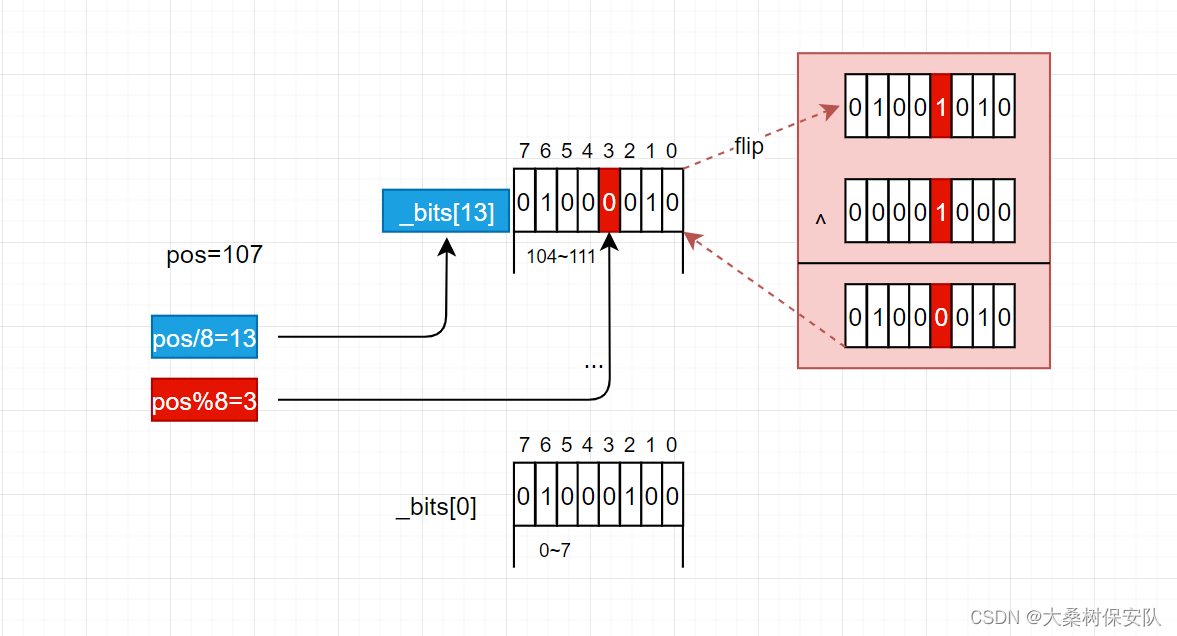
在这里插入图片描述 

void flip(size_t pos)
{
    size_t i=pos/8;
    size_t j=pos%8;

    _bits[i]^=(1<<j);
}



count

count 获取位图中被设置的位的个数，遍历每一个char，统计每个char中的二进制位1的个数

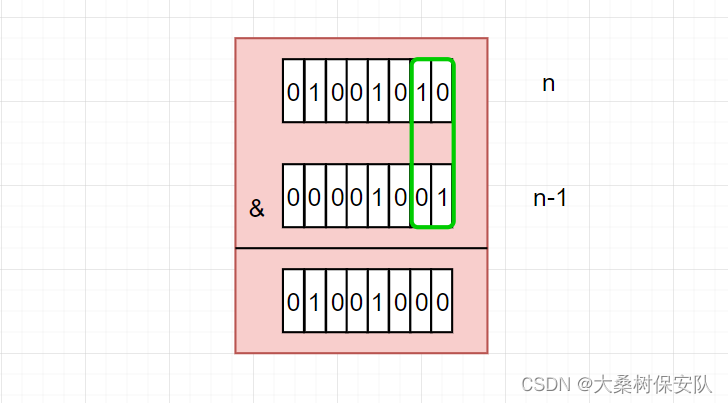
统计二进制中1的个数的方法：

  1. n = n & (n-1) => 消去n的二进制数中最右边的1；
  2. n不为零继续执行第一步；
  3. 执行了几次说明n中有多少个1；

在这里插入图片描述 

size_t count()
{
    size_t count;
    for(auto e:_bits)
    {
        int n=e;
        while(n)
        {
            n=n&(n-1);
            count++;
        }
    }
    return count;
}



none any all


  • none

遍历每一个char 如果全为0，则none返回true 

bool none()
{
	//遍历每个char
	for (auto e : _bits)
	{
		if (e != 0) //该整数中有位被设置
			return false;
	}
	return true; //全部整数都是0，则没有位被设置过
}

  • any

是none的逆操作 

bool any()
{
	return !none(); 
}

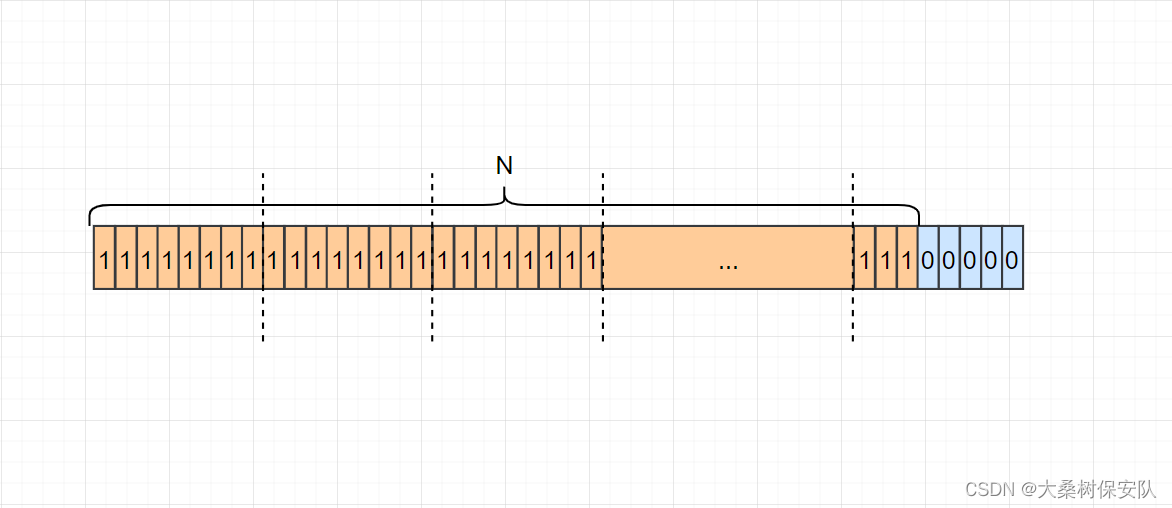
  • all

每一个char中的二进制位全为1，除了最后一个char的剩余的比特位。所以需要分情况：

在这里插入图片描述 

bool all()
{
    size_t size = _bits.size();
    for(size_t i = 0;i < size-1;++i)
    {
        if(~_bits[i]!=0)//取反应该为0，否则取反之前不全为1
            return false;
    }

    for(size_t j = 0;j < NUM % 8 ;++j)
    {
        if((_bits[size-1] & (1<<j))==0)
        {
            return false;
        }
    }
    return true;
}



应用



100亿个整数

给定100亿个整数，设计算法找到只出现1次的整数？

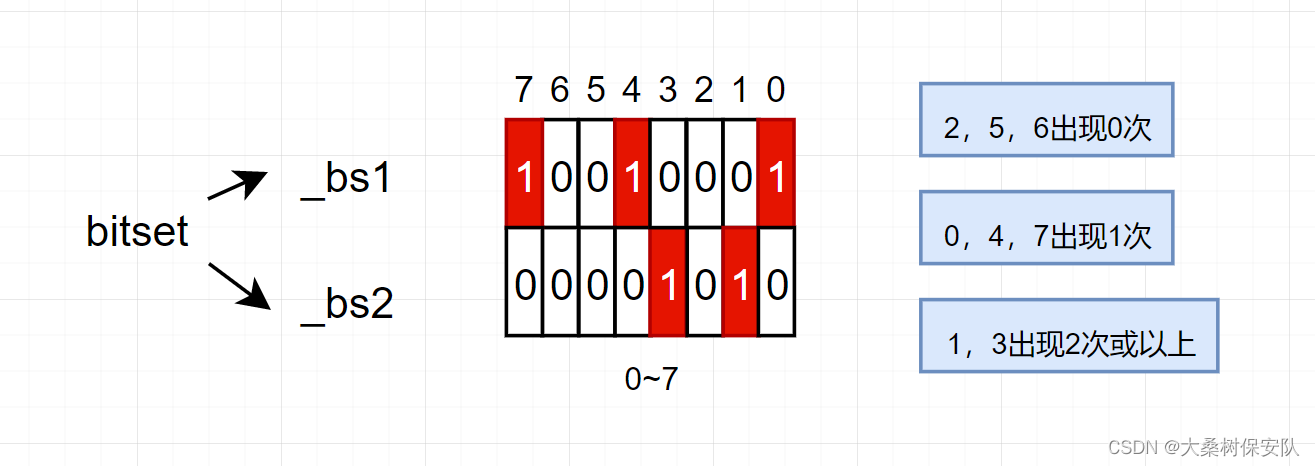
100亿个整数，占用40GB内存，如使用位图将占用512MB内存（因为整型为4字节，不会超过32位，2^32bits=512MB）。整数的出现次数有三种状态

  1. 出现0次
  2. 出现1次
  3. 出现2次及以上

由于一个bit位只能记录两种状态，所以这里需要两个bit位来记录3种状态。我们设计一个类其中封装两个bitset

在这里插入图片描述 

template<size_t N>
	class TwoBitset
	{
	public:
		void set(size_t pos)
		{
			if (!_bs1.test(pos) && !_bs2.test(pos))//00 -> 01
			{
				_bs1.set(pos);
			}
			else if (_bs1.test(pos) && !_bs2.test(pos))//01->10
			{
				//出现次数置为2
				_bs1.reset(pos);
				_bs2.set(pos);
			}
			//10 表示已经出现两次或以上，不用处理
		}

		//找出 出现次数为1（01）的整数,即只出现一次
		void PrintOnceNum()
		{
			for (size_t i = 0; i < N; ++i)
			{
				if (_bs1.test(i))
				{
					cout << i << ' ';
				}
			}
		}

	private:
		std::bitset<N> _bs1;
		std::bitset<N> _bs2;
	};



文件交集

给你两个文件，每个文件分别有100亿个整数，1G可用内存，如何找到两个文件的交集？


答1

：使用哈希函数将第一个文件中的所有整数映射到1000个文件中，如何哈希函数分配合理，那么每个文件几乎可以均匀的分到1000万个整数（4Bytes * 10 * 1000 * 1000 =40MB），将这1000个文件记为a1，…，a1000。同理将第二个文件也利用哈希函数均分1000个文件记为b1，…,b1000。由于是使用同一个哈希函数，两个文件一样的整数会被分到文件下标一致的文件中，那么分别对a1和b1求交集，…,a1000和b1000求交集，每次比较只会占用80MB内存，最后将交集的结果汇总即可。


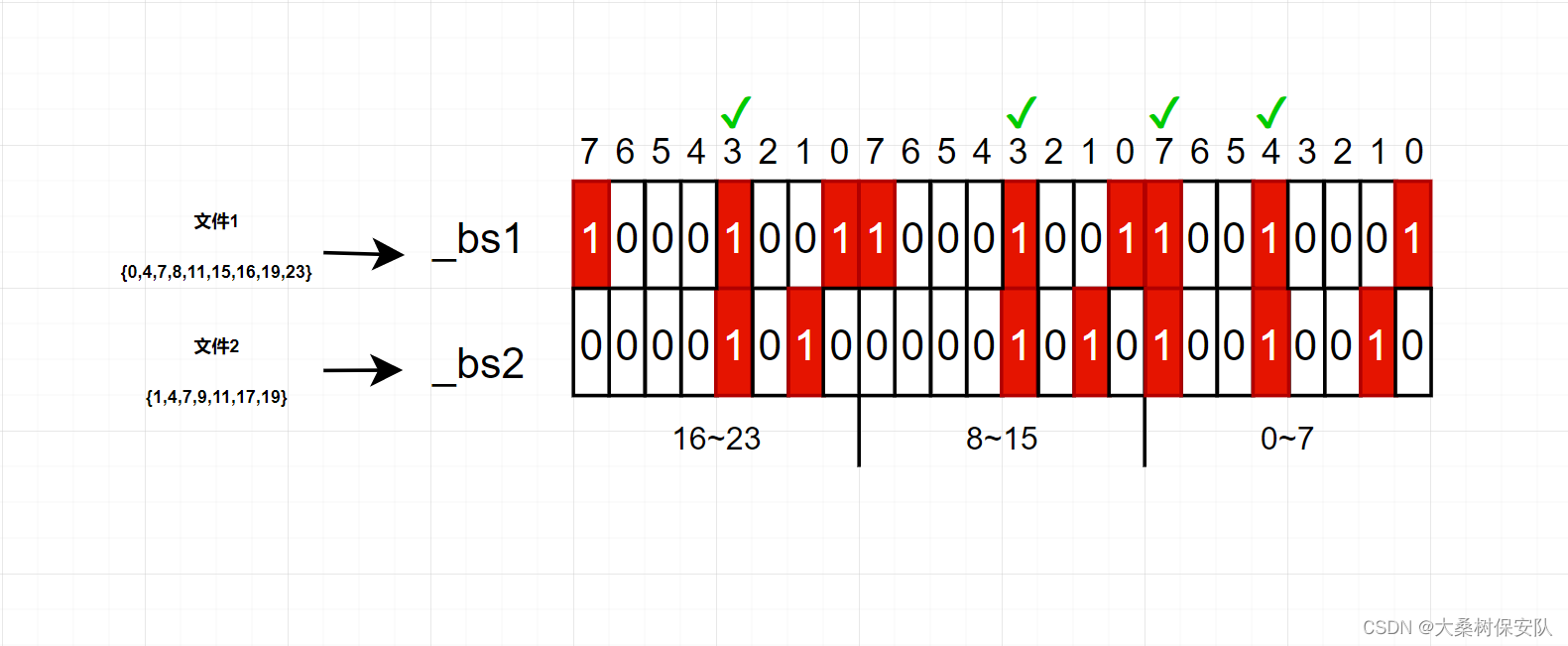
答2

：还是使用位图的方法，分别使用两个位图记录整数是否出现。最后将遍历两个位图，每位按位与运算，如果结果为true则说明为交集整数。

在这里插入图片描述



100亿个整数 1G可用内存

1个文件有100亿个int，1G可用内存，设计算法找到出现次数不超过两次的所有整数

两个位图

  1. 出现0次 ：00
  2. 出现1次 ：01
  3. 出现2次 ：10
  4. 出现3次及以上 ：11

这里出现了四种状态，需要两个位图即可解决；

以此类推如果题目要求为找出不超过5次的整数，那么3个位图可描述8个状态，可以应付这种要求。

— end —


青山不改 绿水长流


版权声明：本文为qq_43041053原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。