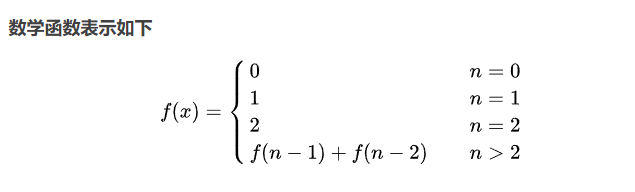? 前言
Wassup guys,我是你们的
机哥
?
(好几个朋友发私信都叫我
机哥
)
今天是C语言每日一练,第90天!
Let’s get it!

文章目录
1. 基础问题
? 题目描述
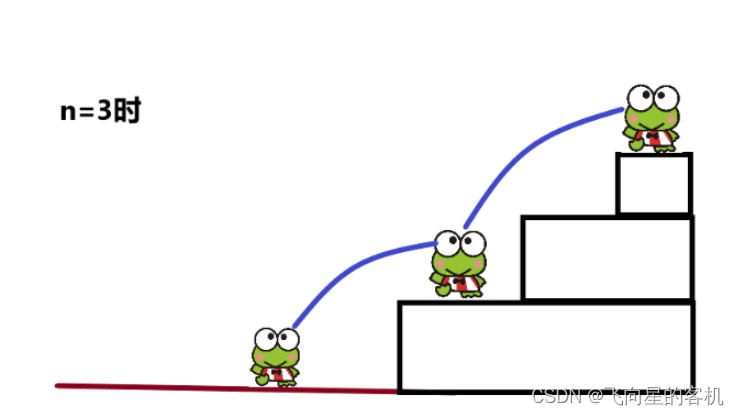
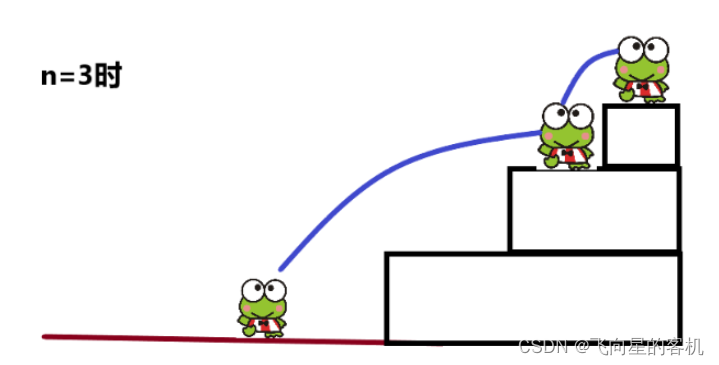
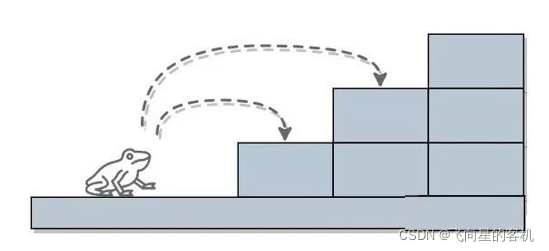
一只青蛙一次可以跳上 1 级台阶,也可以跳上 2 级。求该青蛙跳上一个 n 级的台阶总共有多少种跳法。
诺,就像下面这样?
? 解题思路
其实我一看到这道题,我也是懵的?,不知道从哪里着手分析,那我们就从最简单的情况开始分析。
假如
n = 1
,一共有一级台阶,显然就只有一种跳法
一次跳1阶
;?
假如
n = 2
,一共有两级台阶,共有两种跳法
跳1阶,再跳1阶
?
跳2阶
?
假设
n = 3
,共有三种跳法。
跳1阶,跳1阶,再跳1阶
?
跳1阶,再跳2阶
?
跳2阶, 再跳1阶
?
(
注:此过程图是我从网上找的,实在是难得画啦
?)
通过上面的分析,我们可以这样思考问题?
前往楼梯顶部的最后一步,
要么跳1阶
,
要么跳2阶
;
先假设
f(
n
)
f(n)
f
(
n
)
为
n
级台阶的总跳法数;那么第一次如果选择跳一级的话,剩下的
n-1
级台阶的跳法数就为
f(
n
−
1
)
f(n-1)
f
(
n
−
1
)
。如果第一次跳两级的话,剩下的
n-2
级台阶的跳法就是
f(
n
−
2
)
f(n-2)
f
(
n
−
2
)
;现在青蛙一次只能跳一级或两级,所以我们可以推出以下公式:
咦,这玩意儿不就是我们
斐波那契数
吗??只不过有一点不同的是,斐波那契数列一般是以
1,1,2,3,5,8,13……
开始的;而我们这是以
1,2,3,5,8,13……
开始的,少了最前面的一个1。
? 代码实现
上面说到这个过程有点类似于斐波那契数,但又不完全是,所以我们先看主代码部分?
#include <stdio.h>
int jump(int n)
{
if (n < 3)
{
//假设n的范围是[0, 3]
return n;
}
else
{
//n>3的时候
return jump(n - 1) + jump(n - 2);
}
}
int main()
{
int num = 0;
printf("请输入一个台阶数:> ");
scanf("%d", &num);
int ret = jump(num);
printf("小青蛙有 %d种 跳法\n", ret);
return 0;
}
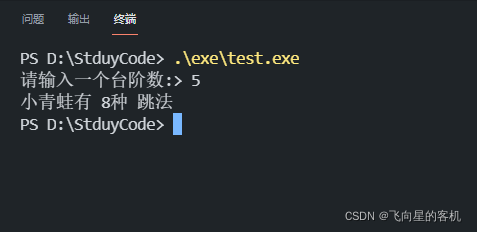
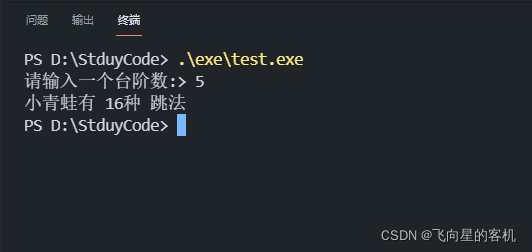
运行结果?
但是,我们来看一下计算的过程?要计算
f(
6
)
f(6)
f
(
6
)
,就需要先计算出子问题
f(
5
)
f(5)
f
(
5
)
和
f(
4
)
f(4)
f
(
4
)
然后要计算
f(
5
)
f(5)
f
(
5
)
,又要先算出子问题
f(
4
)
f(4)
f
(
4
)
和
f(
3
)
f(3)
f
(
3
)
,以此类推。一直到
f(
2
)
f(2)
f
(
2
)
和
f(
1
)
f(1)
f
(
1
)
,递归树才终止。因此,青蛙跳阶,递归解法的时间复杂度 等于
O(
1
)
∗
O
(
2
n
)
=
O
(
2
n
)
O(1) * O(2^n) = O(2^n)
O
(
1
)
∗
O
(
2
n
)
=
O
(
2
n
)
你仔细观察这颗递归树,你会发现存在「大量重复计算」;比如
f(
4
)
f(4)
f
(
4
)
被计算了两次,
f(
3
)
f(3)
f
(
3
)
被重复计算了3次…所以这个递归算法低效的原因,就是存在大量的重复计算!
所以我们可以对代码进行优化
? 递归升级
在递归法的基础上,新建一个长度为
nn
n
的数组,用于在递归时存储
f(
0
)
f(0)
f
(
0
)
至
f(
n
)
f(n)
f
(
n
)
的数字值,重复遇到某数字时则直接从数组取用,避免了重复的递归计算。所以我们设置一个数组,用于存放第一次计算某一个
nn
n
的
jump(n)
。当每一次要计算一个
jump(n)
的时候,就先查看数组中以
nn
n
为下标的地方是否有值,有的话就可以不调用
jump(n)
,而直接从数组中取得结果值,否则再计算
jump(n)
。
?代码实现
#include <stdio.h>
long int f[1000]={0};
int jump(int n){
//当只有一阶台阶的时候,只有一种上台阶的方式。
//当有2阶台阶的时候,有2种上台阶的方式,一种是一次上一阶,还有一种是一次上2个台阶。
//现在设有n阶台阶,如果n>2,那种应该有(先跳一阶)+(先跳2阶)的方式
//如果先跳一阶,那么就有jump(n-1)中方式。如果先跳2阶,那么就有jump(n-2)中方式。
//因此可以知道共有jump(n-1) + jump(n-2)种方式。
if(n==1)
{
f[1]=1;
return f[1];
}
if(n==0)
{
f[0]=1;
return f[0];
}
if(n==2)
{
f[2]=2;
return f[2];
}
else
{
if(f[n-1]!=0)
{
if(f[n-2]!=0)
{
return (f[n-1]+f[n-2]);
}
else
{
f[n-2]=jump(n-2);
return (f[n-1]+f[n-2]);
}
}
else
{
if(f[n-2]!=0)
{
f[n-1]=jump(n-1);
return (f[n-1]+f[n-2]);
}
else
{
f[n-1]=jump(n-1);
f[n-2]=jump(n-2);
return (f[n-1]+f[n-2]);
}
}
}
}
int main()
{
int num = 0;
printf("请输入一个台阶数:> ");
scanf("%d", &num);
int ret = jump(num);
printf("小青蛙有 %d种 跳法\n", ret);
return 0;
}
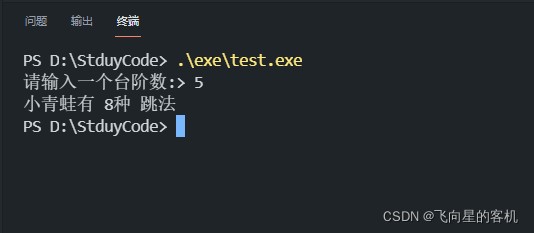
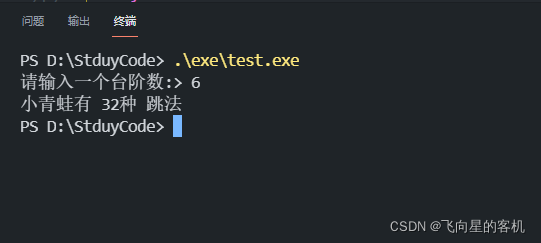
运行结果?
? 动态规划解法
很快我又发现,不必把所有的记录都记起来;
假设我有3阶楼梯,我只需要知道
跳2阶
和
跳1阶
的方法数是多少就可以算出跳3阶的方法数;因此每次只需要保留
n−
1
n-1
n
−
1
阶
和
n−
2
n-2
n
−
2
阶
的方法数。
?代码实现
#include <stdio.h>
int jump(int n)
{
//n=0、1、2的时候,直接返回n即可
if (n < 3)
{
return n;
}
//第一个数为1
int one = 1;
//第二个数为2
int two = 2;
//用于存放前两个数之和
int sum = 0;
while (n > 2)
{
sum = one + two;
one = two;
two = sum;
n--;
}
return sum;
}
int main()
{
int num = 0;
printf("请输入一个台阶数:> ");
scanf("%d", &num);
int ret = jump(num);
printf("小青蛙有 %d种 跳法\n", ret);
return 0;
}
运行结果?
2. 问题升级
? 题目描述
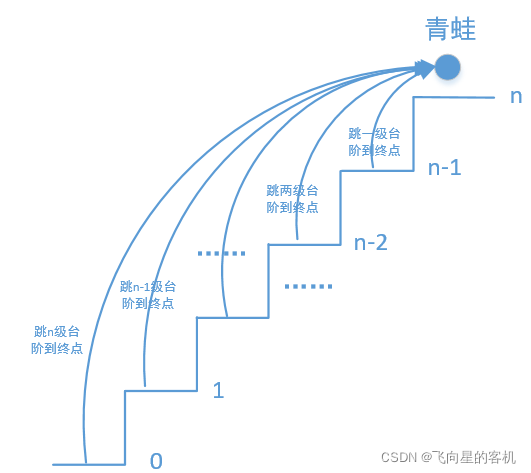
一只青蛙一次可以跳上一级台阶,也可以跳上二级台阶……,
也可以跳n级
,求该青蛙跳上一个n级的台阶总共需要多少种跳法。
? 解题思路
一只青蛙要想跳到n级台阶,可以从一级,二级……,也就是说可以从任何一级跳到n级?
当台阶为1级时,
f(
1
)
=
1
f(1)=1
f
(
1
)
=
1
;当台阶为2级时,
f(
2
)
=
1
+
1
=
2
f(2)=1+1=2
f
(
2
)
=
1
+
1
=
2
;当台阶为3级时,
f(
3
)
=
f
(
1
)
+
f
(
2
)
+
1
=
4
f(3)=f(1)+f(2)+1=4
f
(
3
)
=
f
(
1
)
+
f
(
2
)
+
1
=
4
;当台阶为4级时,
f(
4
)
=
f
(
1
)
+
f
(
2
)
+
f
(
3
)
+
1
=
8
f(4)=f(1)+f(2)+f(3)+1=8
f
(
4
)
=
f
(
1
)
+
f
(
2
)
+
f
(
3
)
+
1
=
8
;当台阶为5级时,
f(
5
)
=
f
(
1
)
+
f
(
2
)
+
f
(
3
)
+
f
(
4
)
+
1
=
16
f(5)=f(1)+f(2)+f(3)+f(4)+1=16
f
(
5
)
=
f
(
1
)
+
f
(
2
)
+
f
(
3
)
+
f
(
4
)
+
1
=
1
6
;所以递推公式我们很容易就能想到:
f(
n
)
=
f
(
n
−
1
)
+
f
(
n
−
2
)
+
…
…
+
f
(
2
)
+
f
(
1
)
+
f
(
0
)
f(n)=f(n-1)+f(n-2)+……+f(2)+f(1)+f(0)
f
(
n
)
=
f
(
n
−
1
)
+
f
(
n
−
2
)
+
…
…
+
f
(
2
)
+
f
(
1
)
+
f
(
0
)
最后这个
f(
0
)
f(0)
f
(
0
)
是可以去掉的,因为0级就相当于没跳,所以
f(
0
)
=
0
f(0)=0
f
(
0
)
=
0
然后我们把
f(
0
)
f(0)
f
(
0
)
去掉再转换一下:
f(
n
−
1
)
=
f
(
n
−
2
)
+
f
(
n
−
3
)
+
…
…
+
f
(
2
)
+
f
(
1
)
f(n-1)=f(n-2)+f(n-3)+……+f(2)+f(1)
f
(
n
−
1
)
=
f
(
n
−
2
)
+
f
(
n
−
3
)
+
…
…
+
f
(
2
)
+
f
(
1
)
;
推导过程?
我们列两个等式:
①
f(
n
)
=
f
(
n
−
1
)
+
f
(
n
−
2
)
+
f
(
n
−
3
)
+
…
+
f
(
2
)
+
f
(
1
)
f(n) = f(n-1) + f(n-2) +f(n-3) + … + f(2) + f(1)
f
(
n
)
=
f
(
n
−
1
)
+
f
(
n
−
2
)
+
f
(
n
−
3
)
+
…
+
f
(
2
)
+
f
(
1
)
②
f(
n
−
1
)
=
f
(
n
−
2
)
+
f
(
n
−
3
)
+
…
+
f
(
2
)
+
f
(
1
)
f(n-1) = f(n-2) +f(n-3) + … + f(2) + f(1)
f
(
n
−
1
)
=
f
(
n
−
2
)
+
f
(
n
−
3
)
+
…
+
f
(
2
)
+
f
(
1
)
由①-②得,
f(
n
)
=
2
f
(
n
−
1
)
f(n) = 2f(n-1)
f
(
n
)
=
2
f
(
n
−
1
)
? 代码实现
? 递归方法
?代码示例
int jump(int n)
{
if (n == 1)
{
return 1;
}
else
{
return 2 * jump(n - 1);
}
}
int main()
{
int num = 0;
printf("请输入一个台阶数:> ");
scanf("%d", &num);
int ret = jump(num);
printf("小青蛙有 %d种 跳法\n", ret);
return 0;
}
运行结果?
? 非递归方法
当然这里也可以用非递归的方式来实现
那么非递归怎么去思考呢?
可以这样理解:
f(
1
)
=
1
=
2
0
f(1) = 1 = 2^0
f
(
1
)
=
1
=
2
0
f(
2
)
=
1
+
f
(
1
)
=
2
=
2
1
f(2) = 1 + f(1) = 2 =2^1
f
(
2
)
=
1
+
f
(
1
)
=
2
=
2
1
f(
3
)
=
1
+
f
(
2
)
+
f
(
1
)
=
4
=
2
2
f(3) = 1 + f(2) + f(1) =4 = 2^2
f
(
3
)
=
1
+
f
(
2
)
+
f
(
1
)
=
4
=
2
2
f(
4
)
=
1
+
f
(
3
)
+
f
(
2
)
+
f
(
1
)
=
8
=
2
3
f(4) = 1 + f(3) + f(2) + f(1) = 8 =2^3
f
(
4
)
=
1
+
f
(
3
)
+
f
(
2
)
+
f
(
1
)
=
8
=
2
3
…
f(
n
)
=
2
(
n
−
1
)
f(n)=2^{(n-1)}
f
(
n
)
=
2
(
n
−
1
)
;然后使用用函数
pow(2,n -1)
,需要加头文件
<math.h>
但是我们这里可以不用库函数来实现,给大家介绍一种神奇的运算
?代码示例
int jump(int n)
{
if (n == 1)
{
return 1;
}
else
{
return 1 << (n-1);
}
}
int main()
{
int num = 0;
printf("请输入一个台阶数:> ");
scanf("%d", &num);
int ret = jump(num);
printf("小青蛙有 %d种 跳法\n", ret);
return 0;
}
运行结果?
我这里选择用
<<
左移操作符来计算
3. 特性总结
其实这道算法题的本质可以说就是斐波那契数的衍生;
反言之,对于算法,我的理解:
算法本质就是数学的解题过程