第一部分 程序结构和执行
我认为学会一个东西不能靠死记硬背,唯有把握了核心性质才能抓住问题关键,真正掌握这个知识,所以我尽量给大家理清核心性质
这一部分等全写完再补上
第一章 信息的表示和处理
2.1信息的存储
机器级程序将存储器视为一个非常大的字节数组,成为虚拟存储器。
每个字节都有唯一的数字标识,称为地址。
2.1.1 十六进制表示法

2.1.2 字
字长决定虚拟地址空间的大小,大小为0-
2
n
−
1
2^{n-1}
2
n
−
1
n是代表位数,我们常说的32位操作系统64位操作系统的内存最大就是
2
n
−
1
2^{n-1}
2
n
−
1
,也就是4GB和8GB。
2.1.3 数据大小

2.1.4 寻址和字节顺序
两种方法,大端法、小端法

最低有效字节在最前面叫小端法,最高有效字节在前面较大端法
2.1.5表示字符串
每一个char字符都有一个对应的ASCLL值,以0x00结尾
2.1.6 表示代码
程序只是字节序列,机器没有关于源程序的任何信息
2.1.7 布尔代数简介
涉及到了| & ^ ~ 四种符号
|是对两数字每一相同位存在1则为1,否则为0
&对两数字每一相同位上都为以1则为1,否则为0
^ 同0异1
~ 所有位都取反

2.1.8 C语言位级运算
C语言的位运算可以运用到任何整形数据类型中。
2.1.9 C语言逻辑运算
C语言中有|| 、&& 、!,这些逻辑运算符。
进行运算时只有0是false,其他都为true;
2.1.10 C语言中移位运算
右移分为算数右移和逻辑右移,算数右移最左侧为1的时候需要在最左侧补上一个1,这与补码的表示有关,而unsigned进行算数右移时会出现bug,只能进行逻辑右移,而 c语言没有对算数右移和逻辑右移做出明确规定,所以存在潜在bug。
此小节理解起来需要补码的知识,暂时理解不了也没关系。
java中明确规定了>>为算数右移,>>>为逻辑右移。
2.2整数表示
2.2.1整数数据类型

记住64位操作系统就行,然后int是
1
0
9
10^9
1
0
9
级别,long long是
1
0
18
10^{18}
1
0
1
8
,在算法题中常用,还有一个数值是log(
1
e
9
1e9
1
e
9
)≈30,在算时间复杂度时常用。
2.2.2 无符号数编码

简而言之就是每一个01序列对应的数字都是唯一的,每一个在范围内的数字对应唯一的01序列。
2.2.3 补码编码
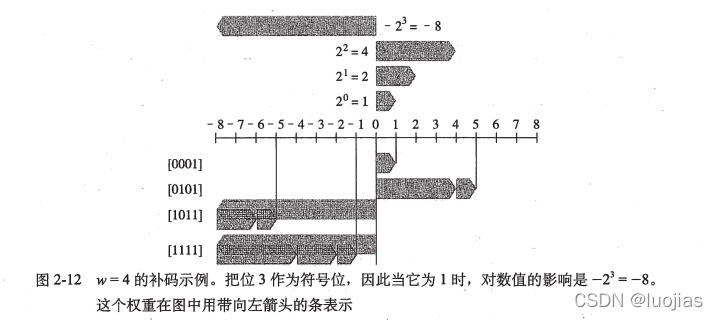
补码
按照书中说法,补码就是把最高位的向量方向向后指,从而能够表示负数,也就是最高位是1就是负数。

这两个公式对于理解反码原码本质十分重要
反码就是在补码的基础上将最高位权值-1;
原码则是最高位决定正负
2.2.4有符号数和无符号数之间的转换
在原文中给出了十分严谨的数学证明,其实证明的是一个浅显的道理,计算机按照不同的方式输出有符号数和无符号数,由于最高位的权值是相反的,所以值也是不同的。
这个公式也很好证明

最高位为1的时候值是大于
2
w
−
1
2^{w-1}
2
w
−
1
,所以减去
2
∗
2
w
−
1
2*2^{w-1}
2
∗
2
w
−
1
就是所求的有符号数。
2.2.5 C语言中的有符号数和无符号数
主要是一点:
c语言进行运算的时候,会将有符号数转变为无符号数
2.2.6 扩展一个数字的位表示
在补码情况下,拓展一个数字,只需要在需要拓展的最高位变为当前最高位上的数字即可。
因为有一个核心性质,当拓展的位数是0的时候直接加0。
但如果需要拓展的位数是1的时候,在最高位新添加1,数字的值会进行如下变化:(
−
2
n
+
2
∗
2
n
−
1
-2^{n}+2*2^{n-1}
−
2
n
+
2
∗
2
n
−
1
)。
第一个
−
2
n
-2^{n}
−
2
n
是最高位新添加的1,而在次高位的值从
−
2
n
−
1
-2{n-1}
−
2
n
−
1
变成了
2
n
−
1
2^{n-1}
2
n
−
1
,所以大小没有改变,能够以这种方式进行拓展。
2.2.7 截断数字
截断数字其实是一种取模运算,然后根据所截得的数字是有符号数还是无符号数,来确定是否使用上图的公式。
2.2.8关于有符号数和无符号数的建议
尽量避免两者混淆使用。
2.3 整数运算
2.3.1无符号数加法

相当于对
2
w
2^w
2
w
取模
2.3.2补码加法

先按正常进行计算然后删去前面的位数即可。
补码加法其实本质上也是一种取模运算,截断运算。
2.3.3补码的非
就是所有位取反后加1,证明如下:
当一个数是负数时,我们可以看成其他位为0的位的值的和-1,就是负数的值,而变为正数后,其他为0的位变为1,也就是为1的位的值得和+1就位正数的值。
同理,而当一个数为正数时,值可以看成为1的数的和,而负数则是为0的数的和-1,当正数取反后,所有1变成0,得到的数为正数取反-1.
所以就会出现一个问题当一个数除负数位之外的其他位全为0的时候变为相反数时还会是眼来的负数。
2.3.4无符号乘法

跟这个同时的原理相同
2.3.5补码乘法
补码乘法也是一种取模运算。
补码乘法在cpu中怎么进行的可以参考
这篇文章
2.3.6 乘以常数
文章向我们说明了,可以将乘法变为移位和加法进行计算。

2.3.7除以2的幂
(1)除以2可以看做是向右移位。
(2)除以负数时需要向0取整,则需要加上偏移量
2
k
−
1
2^k-1
2
k
−
1
,则变为
(
x
+
2
k
−
1
)
>
>
2
k
(x+2^k-1)>>2^k
(
x
+
2
k
−
1
)
>
>
2
k
可以简单证明出:当x能被整除时会得
x
/
2
k
x/2^k
x
/
2
k
,而不能整除时会得到
x
/
2
k
−
1
x/2^k-1
x
/
2
k
−
1
因为只要x有余数后面的偏移量加上余数除
2
k
2^k
2
k
必定会得到一个大小为1的数。
(3)该方法不能像乘法一样推广到任意常数
2.4浮点数
2.4.1二进制小数
二进制小数的表示:

2.4.2IEEE浮点表示
浮点标准:
(
−
1
)
s
∗
M
∗
2
e
(-1)^s*M*2^e
(
−
1
)
s
∗
M
∗
2
e
s是符号位,1代表负数,2代表正数
这部分证明非常复杂,后序找个时间单独写一篇关于浮点数的文章。
本文参考书籍深入理解计算机系统