一、角点检测
特征点检测广泛应用到目标匹配、目标跟踪等应用中,在进行目标建模时会对图像进行目标特征的提取,常用的有颜色、角点、特征点、轮廓、纹理等特征。其中Harris角点检测是特征点检测的基础,提出了应用邻近像素点灰度差值概念,从而进行判断是否为角点、边缘、平滑区域。
Harris角点检测原理是利用移动的窗口在图像中计算灰度变化值,算法基本思想是使用一个固定窗口在图像上进行任意方向上的滑动,比较滑动前与滑动后两种情况,窗口中的像素灰度变化程度,如果存在任意方向上的滑动,都有着较大灰度变化,那么计算机就认为该窗口中存在角点。
———————————————————————————————————————————
二、角点特征
角点是一幅图像上最明显与重要的特征,对于一阶导数而言,角点在各个方向的变化是最大的,而边缘区域在只是某一方向有明显变化。该点附近区域的像素点无论在梯度方向上还是其梯度幅值上有着较大变化:

在平坦区域上,窗口向各个方向移动均没有明显的梯度变化

在边缘区域内,窗口向平行于边缘方向移动,图像梯度变化不大,垂直于边缘方向移动,图像梯度变化很大。
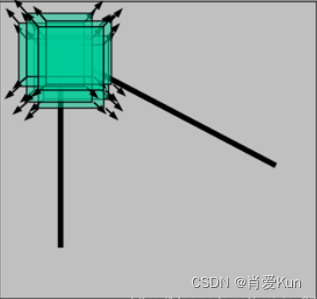
在角度区域内,窗口向任意方向移动,图像梯度的变化有着明显变化
———————————————————————————————————————————
三、Harris角点检测数学原理
Harris角点检测是通过数学计算在图像上发现角点特征的一种算法,而且其具有旋转不变性的特质。角点是一幅图像上最明显与重要的特征,对于一阶导数而言,角点在各个方向的变化是最大的,而边缘区域在只是某一方向有明显变化。Harris角点检测基本数学公式如下:
公式说明:
公式中
是一个与图像尺寸一样的的一个矩阵;
表示方形的二值窗口,若像素点在窗口内,则取值为1,否则为0;
表示x,y处像素灰度值强度,范围为0~255。任何一个函数表达式,均可有泰勒公式进行展开,以逼近原函数,我们可以对下面函数进行一阶展开。
泰勒公式进行展开:
计算权重
窗口的取值为1,其中
为图像在x方向上和y方向上的图像梯度,可以使用Sobel算子进行求取,Harris角点检测算法原理可以近似为:
对于局部微小的移动量
,可以近似得到下面的表达:
其中M为2*2的矩阵,可由图像的导数求得:
四、harris角点响应函数R
(1)矩阵M,将其对角化之后 ,特征值λ1, λ2 分别代表了X 和Y 方向的灰度变化率.
(2)通过M的两个特征值λ1, λ2的大小对图像点进行分类
如果λ1, λ2都很小, 图像窗口在所有方向上移动都无明显灰度变化。
如果λ1, λ2都很大, 图像窗口在所有方向上移动都产生明显灰度变化
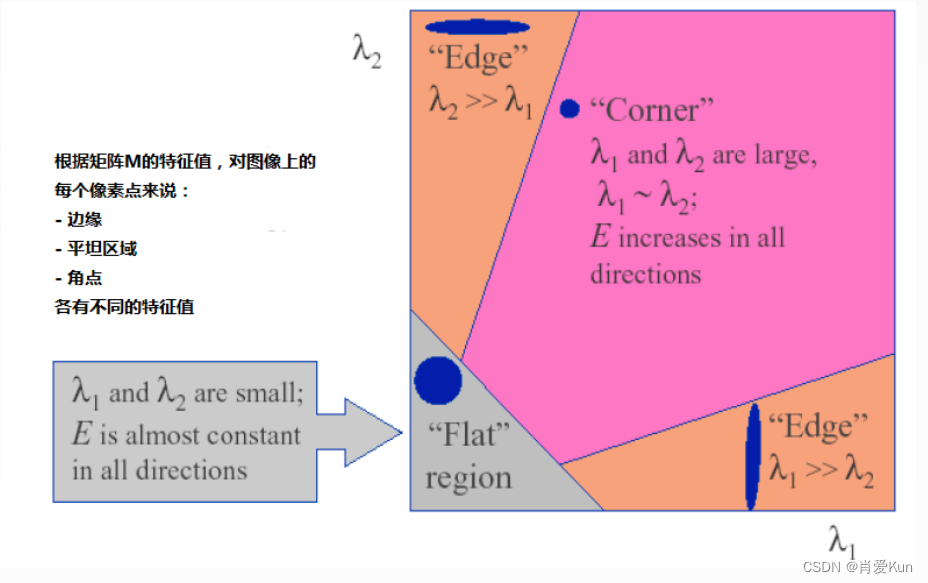
(3)定义角点响应函数R
如下图所示,R只与M的特征值有关,判定关系为,角点:R 为大数值正数;边缘:R为大数值负数;平坦区:R为小数值;
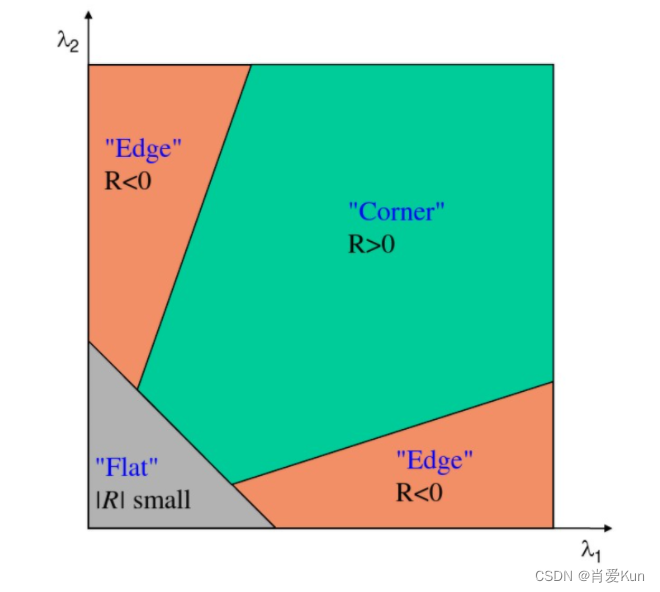
对角点响应函数R进行阈值处理
操作; 当
时,定义为角点,最后对所有提取出的角点进行非极大值抑制,提取R的局部极大值。角点响应函数R对于旋转具有不变性,对于图像的灰度变化具有部分不变性,对于图像尺度变化不8具有不变性。一个好的角点沿着任意方向移动都将导致明显的图像灰度变化,即:R具有大的正数值,对于k值,我们一般取0.04~0.06。
——————————————————————————————————————————
cornerHarris 函数API接口:
C++:void cornerHarris( InputArray src,
OutputArray dst,
int blockSize,
int ksize,
double k,
int borderType=BORDER_DEFAULT )
参数说明:
第一个参数src,输入8bit单通道灰度Mat矩阵
第二个参数dst, 用于保存Harris角点检测结果,32位单通道,大小与src相同
第三个参数blockSize, 滑块窗口的尺寸
第四个参数ksize, Sobel边缘检测滤波器大小
第五个参数k,Harris中间参数,经验值0.04~0.06
第六个参数bordertype,插值类型
———————————————————————————————————————————
代码实现
#include"stdafx.h"
#include <opencv2/opencv.hpp>
#include <iostream>
using namespace cv;
using namespace std;
Mat src, gray_src;
int thresh = 130;
int max_count = 255;
const char* output_title = "HarrisCornerDetection Result";
void Harris_Demo(int, void*);
int main(int argc, char** argv) {
src = imread("F:/photo/jz.jpg");
if (src.empty()) {
printf("could not load image...\n");
return -1;
}
namedWindow("input image", WINDOW_AUTOSIZE);
imshow("input image", src);
namedWindow(output_title, WINDOW_AUTOSIZE);
cvtColor(src, gray_src, COLOR_BGR2GRAY);
createTrackbar("Threshold:", output_title, &thresh, max_count, Harris_Demo);
Harris_Demo(0, 0);
waitKey(0);
return 0;
}
void Harris_Demo(int, void*) {
Mat dst, norm_dst, normScaleDst;
dst = Mat::zeros(gray_src.size(), CV_32FC1);
int blockSize = 2;
int ksize = 3;
double k = 0.04;
cornerHarris(gray_src, dst, blockSize, ksize, k, BORDER_DEFAULT);
normalize(dst, norm_dst, 0, 255, NORM_MINMAX, CV_32FC1, Mat());
convertScaleAbs(norm_dst, normScaleDst);
Mat resultImg = src.clone();
for (int row = 0; row < resultImg.rows; row++) {
uchar* currentRow = normScaleDst.ptr(row);
for (int col = 0; col < resultImg.cols; col++) {
int value = (int)*currentRow;
if (value > thresh) {
circle(resultImg, Point(col, row), 2, Scalar(0, 0, 255), 2, 8, 0);
}
currentRow++;
}
}
imshow(output_title, resultImg);
}———————————————————————————————————————————
图像处理效果
threshold = 130时的图像效果

threshold = 130时的图像效果
