字符串匹配算就是给定两个串，查找一个串是否在另一个串里面。为解决这个问题由此衍生了两个算法，B BF 算法和 KMP 算法。下面就来了解一下这两个算法吧。

1.用java实现 BF 算法

BF算法又称为暴力算法，它的核心思想是：从下标为 0 处比较主串和子串，若相等，则依次向下比较，直到子串结束，则得到匹配结果，若不相等，则主串回溯到下标为 1 处和子串下标为 0 处比较，依次类推，直到得到结果。

优点：比较容易理解，没有对主串和子串进行多余的处理。

缺点：每次

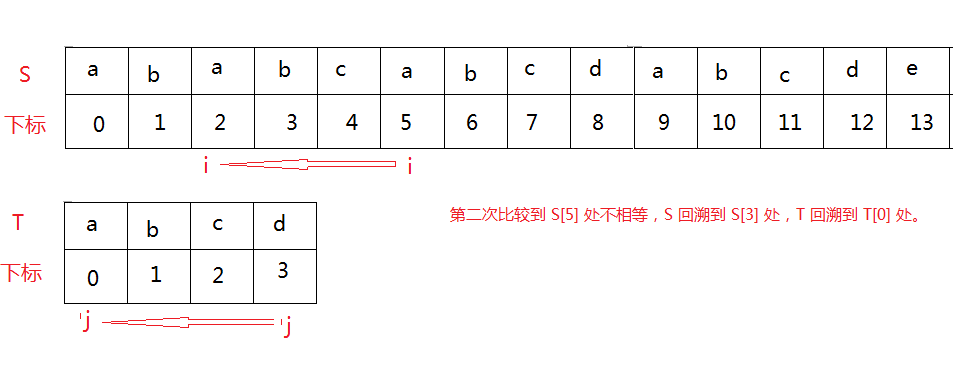
每次字符不匹配时，都要回溯到上次比较的下一个位置，时间开销大。

大家可以按照下面的图来理解比较容易一些。

由此我们发现 i 每次走的位置都等于 j 走的位置，所以我们的到 i 拖回的位置为 i-j+1。

下面用 java 实现 BF 算法的代码。

public static int BF(String str,String sub,int pos){
    //1.判断pos合法性。
    if(pos < 0 || pos > str.length()){
        return -1;
    }
    //2.开始查找。
    int i = pos;
    int j = 0;
    //3.遍历主串和子串。
    while(i <str.length() && j <sub.length()){
        if(str.charAt(i) == sub.charAt(j)){
	    i++;
	    j++;
        }else{
	    i = i-j+1;
	    j = 0;
	}
    }
    //4.哪种情况下表示找到
    if(j >= sub.length()){
	return i-j;
    }else{
        return -1;
    }
}	

下面是运算结果：

public static void main(String[] args) {
    String str = "ababcabcdabcde";
    String sub =  "abcd";
    System.out.println(BF(str,sub,0));
}

2.KMP算法

相比于 BF 算法，KMP 算法时间复杂度大大的减小了，主要在于主串不用回溯。但是 KMP 算法非常难理解，需要仔细琢磨。

我们举例来看。

以下是根据KMP算法写出的代码：

public static int Kmp(String str,String sub,int pos){
	int i = pos;
	int j = 0;
	int[] next = new int[sub.length()];
	getNext(next,sub);
	while(i < str.length() && j < sub.length()){
		if(j == -1 || str.charAt(i) == sub.charAt(j)){
			i++;
			j++;
		}else{
			j = next[j];
		}
	}
	if(j >= sub.length()){
		return i-j;
	}else{
		return -1;
	}
}

那么我们如何来找 j 退回的位置呢，这才是 KMP 算法的核心所在。找到 j 的退回位置有如下规则：

找到匹配成功部分的两个相等的真子串（不包含本身），一个以下标 0 开始，另一个以 j-1 下标结尾。

不管什么数据 next[0] = -1;next[1] = 0;

例如上图：主串前面的 ab 和子串开头的 ab 相等，所以我们直接将 j 退回到 c 的位置，然后比较 i 和 j 位置的字符。

为了得到每个 j 返回的位置，我们需要设一个数组 next 来存储 j 返回的位置。

上图的子串对应的数组即为-1,0,0,0,1,2.

我们推导出如下的公式：

下面是根据这个规则写出的代码：

public static void getNext(int[] next,String str){
	next[0] = -1;
	next[1] = 0;
	int i = 2;//下一项
	int k = 0;//前一项的k
	while(i < str.length()){
		if(k == -1||str.charAt(k) == str.charAt(i - 1)){//Pk == Pi时
			next[i] = k + 1;
			i++;
			k = k+1;
		}else{
			k = next[k];
		}
	}
}

如果有什么不当之处请指出。