(本人笔记潦草,估计只有我能看懂,保存给自己看,不代表肯定让其他人能理解)
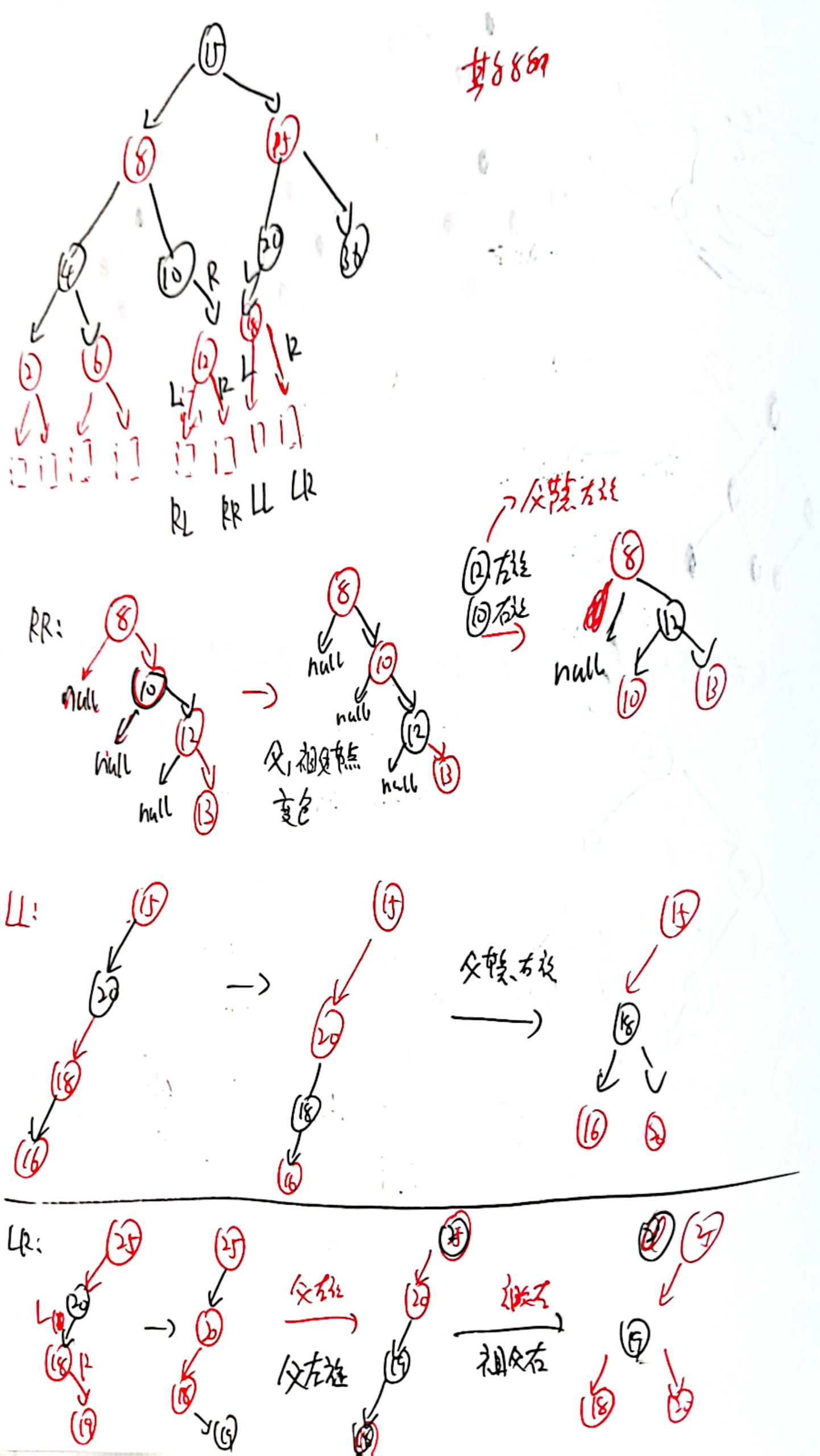
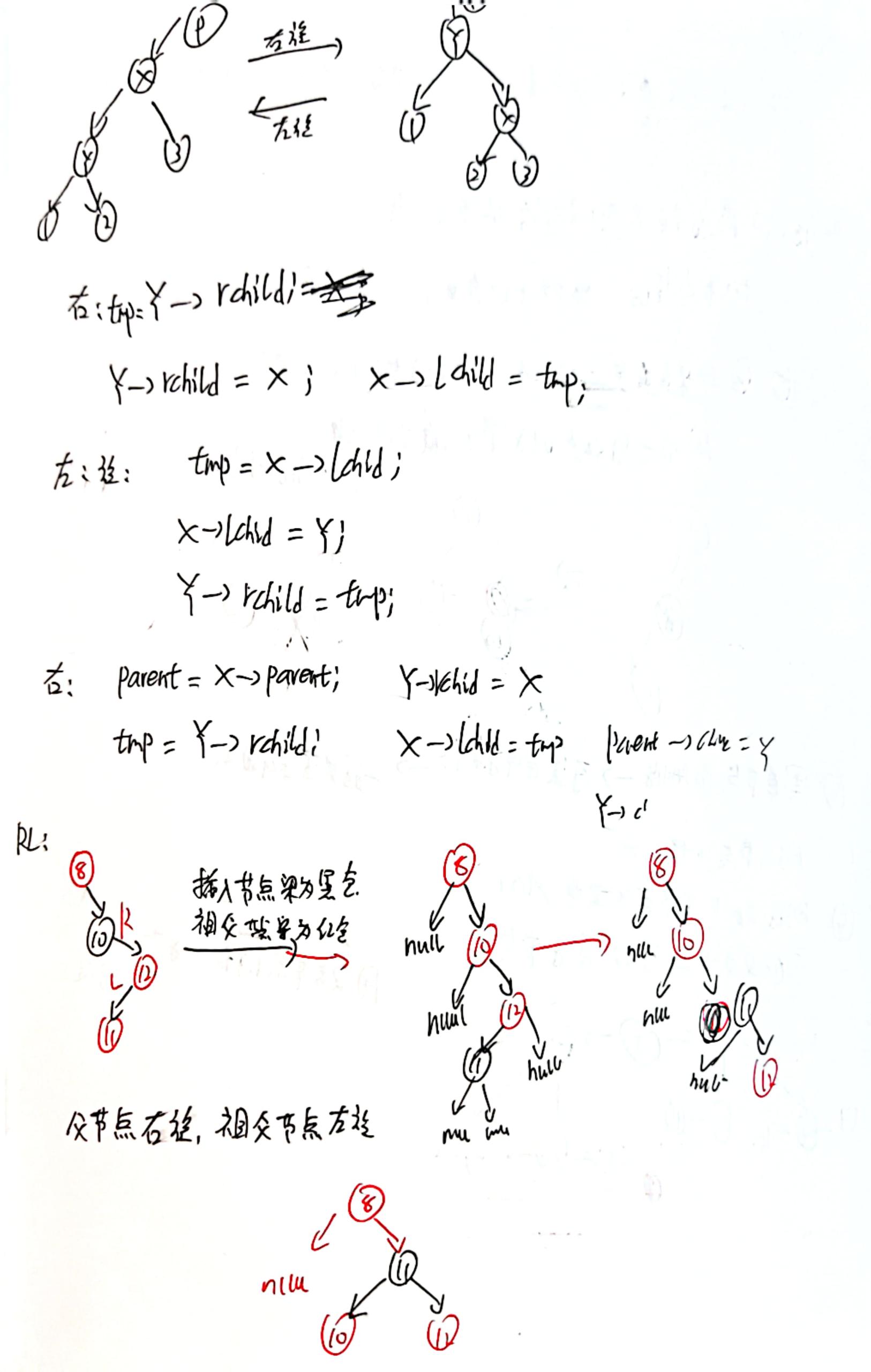

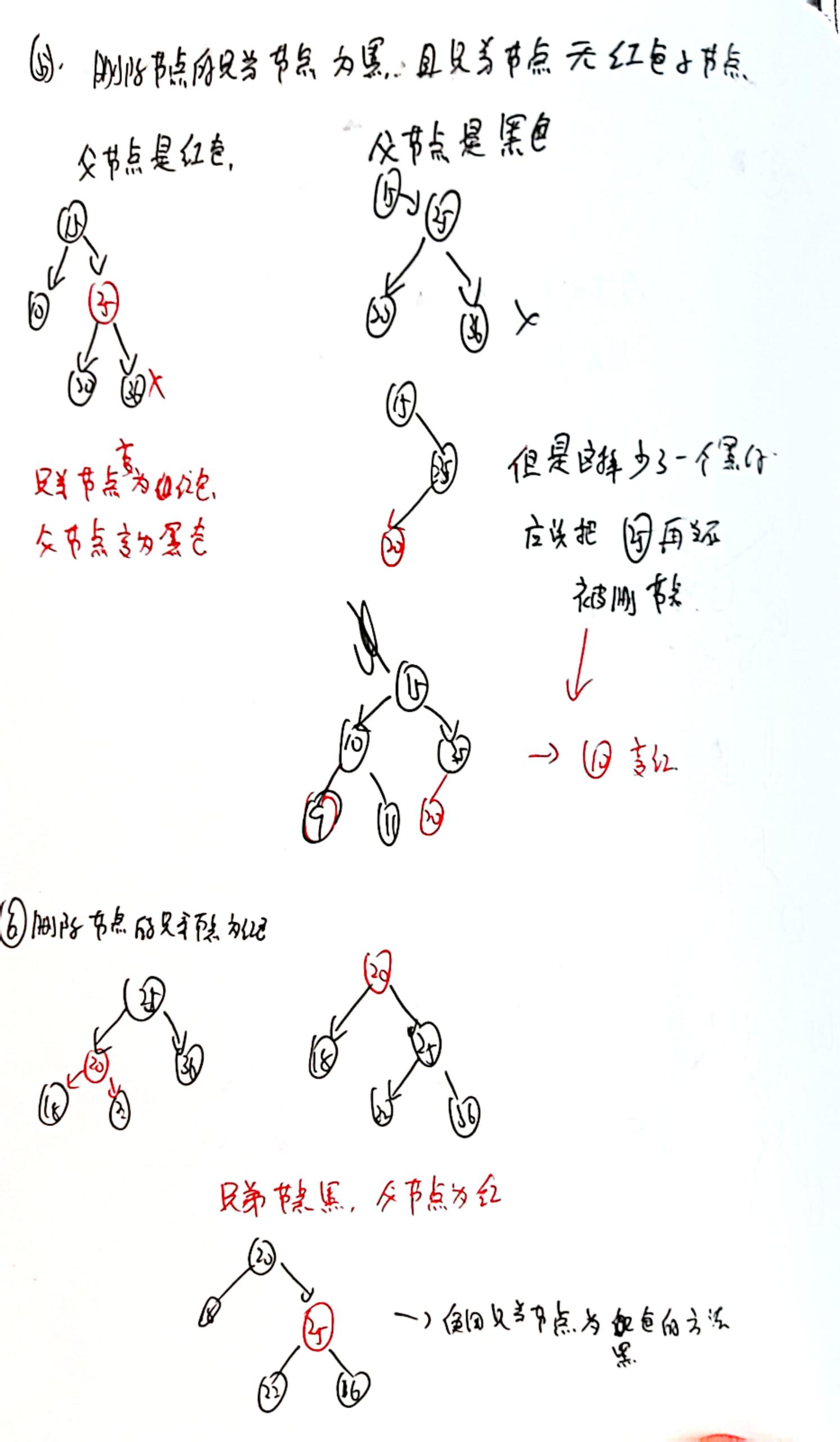
附上源码笔记:
// SPDX-License-Identifier: GPL-2.0-or-later
/*
Red Black Trees
(C) 1999 Andrea Arcangeli <andrea@suse.de>
(C) 2002 David Woodhouse <dwmw2@infradead.org>
(C) 2012 Michel Lespinasse <walken@google.com>
linux/lib/rbtree.c
*/
#include <linux/rbtree_augmented.h>
#include <linux/export.h>
/*
* red-black trees properties: https://en.wikipedia.org/wiki/Rbtree
*
* 1) A node is either red or black
* 2) The root is black
* 3) All leaves (NULL) are black
* 4) Both children of every red node are black
* 5) Every simple path from root to leaves contains the same number
* of black nodes.
*
* 4 and 5 give the O(log n) guarantee, since 4 implies you cannot have two
* consecutive red nodes in a path and every red node is therefore followed by
* a black. So if B is the number of black nodes on every simple path (as per
* 5), then the longest possible path due to 4 is 2B.
*
* We shall indicate color with case, where black nodes are uppercase and red
* nodes will be lowercase. Unknown color nodes shall be drawn as red within
* parentheses and have some accompanying text comment.
*/
/*
* Notes on lockless lookups:
*
* All stores to the tree structure (rb_left and rb_right) must be done using
* WRITE_ONCE(). And we must not inadvertently cause (temporary) loops in the
* tree structure as seen in program order.
*
* These two requirements will allow lockless iteration of the tree -- not
* correct iteration mind you, tree rotations are not atomic so a lookup might
* miss entire subtrees.
*
* But they do guarantee that any such traversal will only see valid elements
* and that it will indeed complete -- does not get stuck in a loop.
*
* It also guarantees that if the lookup returns an element it is the 'correct'
* one. But not returning an element does _NOT_ mean it's not present.
*
* NOTE:
*
* Stores to __rb_parent_color are not important for simple lookups so those
* are left undone as of now. Nor did I check for loops involving parent
* pointers.
*/
static inline void rb_set_black(struct rb_node *rb)
{
rb->__rb_parent_color |= RB_BLACK;
}
static inline struct rb_node *rb_red_parent(struct rb_node *red)
{
return (struct rb_node *)red->__rb_parent_color;
}
/*
* Helper function for rotations:
* - old's parent and color get assigned to new
* - old gets assigned new as a parent and 'color' as a color.
*/
static inline void
__rb_rotate_set_parents(struct rb_node *old, struct rb_node *new,
struct rb_root *root, int color) //在old节点和它的父节点之间插入一个新节点,替换old节点,old节点变成新节点的child
{
struct rb_node *parent = rb_parent(old);
new->__rb_parent_color = old->__rb_parent_color;
rb_set_parent_color(old, new, color);
__rb_change_child(old, new, parent, root);
}
static __always_inline void
__rb_insert(struct rb_node *node, struct rb_root *root, // 红黑树的插入
void (*augment_rotate)(struct rb_node *old, struct rb_node *new))
{
struct rb_node *parent = rb_red_parent(node), *gparent, *tmp; //获得插入节点的父节点,此时已经插入好了,需要变色
while (true) {
/*
* Loop invariant: node is red.
*/
if (unlikely(!parent)) { //如果插入节点的父节点是空,说明是根节点
/*
* The inserted node is root. Either this is the
* first node, or we recursed at Case 1 below and
* are no longer violating 4).
*/
rb_set_parent_color(node, NULL, RB_BLACK); // 根节点染黑,没有父节点
break;
}
// 插入的node一开始默认是红色的
/*
* If there is a black parent, we are done.
* Otherwise, take some corrective action as,
* per 4), we don't want a red root or two
* consecutive red nodes.
*/
if(rb_is_black(parent)) // 1. 如果父亲节点是黑色,直接退出,说明不用改变
break;
// 此时父亲节点肯定是红色了,获得父亲节点的父亲节点,也就是插入节点的祖父节点
gparent = rb_red_parent(parent);
tmp = gparent->rb_right; // 获取祖父节点的右节点
if (parent != tmp) { /* parent == gparent->rb_left */
// 如果tmp是插入节点的叔父节点,父亲节点在左边
if (tmp && rb_is_red(tmp)) { //2.如果叔父节点是红色,此时就是父亲和叔父节点都是红色
/*
* Case 1 - node's uncle is red (color flips).
*
* G g
* / \ / \
* p u --> P U
* / /
* n n
*
* However, since g's parent might be red, and
* 4) does not allow this, we need to recurse
* at g.
*/
// 叔父和父亲节点都变黑
rb_set_parent_color(tmp, gparent, RB_BLACK);
rb_set_parent_color(parent, gparent, RB_BLACK);
// 插入节点变成祖父节点,获取祖父节点的父亲节点,准备重新递归,让祖父节点向上变换颜色
node = gparent;
parent = rb_parent(node);
rb_set_parent_color(node, parent, RB_RED); // 祖父节点染成红色
continue;
} //如果没有走上面的if函数,说明叔父节点为黑色或者为空
tmp = parent->rb_right;
if (node == tmp) { //3. 如果插入节点在有右边,上面判断父亲节点在左边, LR
// 插入节点变黑-->祖父节点变红-->父亲节点左旋-->祖父节点右旋
/*
* Case 2 - node's uncle is black and node is
* the parent's right child (left rotate at parent).
*
* G G
* / \ / \
* p U --> n U
* \ /
* n p
*
* This still leaves us in violation of 4), the
* continuation into Case 3 will fix that.
*/
tmp = node->rb_left; //获取插入节点左边节点
WRITE_ONCE(parent->rb_right, tmp); //父亲节点右边指向tmp
WRITE_ONCE(node->rb_left, parent); //插入节点左边节点指向父亲节点
if (tmp)
rb_set_parent_color(tmp, parent,
RB_BLACK); //插入节点左边节点存在就把父亲节点指向parent
rb_set_parent_color(parent, node, RB_RED);//插入节点变成父亲节点的父亲
augment_rotate(parent, node);
parent = node; // 此时交换,父亲节点变成插入节点,为了下面的LL作准备
// 之前是tmp = parent->rb_right;但是node变成parent了,这里就是node的right
tmp = node->rb_right;
// 此时变成LL
}
// 4.此时变成LL, 父子节点都为红色,祖父节点右旋
/*
* Case 3 - node's uncle is black and node is
* the parent's left child (right rotate at gparent).
*
* G P
* / \ / \
* p U --> n g
* / \
* n U
*/
WRITE_ONCE(gparent->rb_left, tmp); /* == parent->rb_right */ //祖父节点的左边指向父亲节点右边
WRITE_ONCE(parent->rb_right, gparent); //父亲节点右边指向祖父节点
if (tmp)
rb_set_parent_color(tmp, gparent, RB_BLACK);
__rb_rotate_set_parents(gparent, parent, root, RB_RED);//祖父节点的父亲节点指向parent
augment_rotate(gparent, parent);
break;
} else { // 父亲节点是祖父节点的右节点
tmp = gparent->rb_left; //获取叔父节点
if (tmp && rb_is_red(tmp)) {
/* Case 1 - color flips */
rb_set_parent_color(tmp, gparent, RB_BLACK);
rb_set_parent_color(parent, gparent, RB_BLACK);
node = gparent;
parent = rb_parent(node);
rb_set_parent_color(node, parent, RB_RED);
continue; //如果叔父节点是红色,就递归,同上
}
tmp = parent->rb_left;
if (node == tmp) { //当前节点在父亲节点的左边,父亲节点在祖父节点右边,RL
// 父亲节点右旋,祖父节点左旋
/* Case 2 - right rotate at parent */
tmp = node->rb_right;
WRITE_ONCE(parent->rb_left, tmp);
WRITE_ONCE(node->rb_right, parent);
if (tmp)
rb_set_parent_color(tmp, parent,
RB_BLACK);
rb_set_parent_color(parent, node, RB_RED);
augment_rotate(parent, node);
parent = node;
tmp = node->rb_left;
}
/* Case 3 - left rotate at gparent */
WRITE_ONCE(gparent->rb_right, tmp); /* == parent->rb_left */
WRITE_ONCE(parent->rb_left, gparent);
if (tmp)
rb_set_parent_color(tmp, gparent, RB_BLACK);
__rb_rotate_set_parents(gparent, parent, root, RB_RED);
augment_rotate(gparent, parent);
break;
}
}
}
/*
* Inline version for rb_erase() use - we want to be able to inline
* and eliminate the dummy_rotate callback there
*/
static __always_inline void
____rb_erase_color(struct rb_node *parent, struct rb_root *root,
void (*augment_rotate)(struct rb_node *old, struct rb_node *new))
{
struct rb_node *node = NULL, *sibling, *tmp1, *tmp2;
while (true) {
/*
* Loop invariants:
* - node is black (or NULL on first iteration)
* - node is not the root (parent is not NULL)
* - All leaf paths going through parent and node have a
* black node count that is 1 lower than other leaf paths.
*/
sibling = parent->rb_right; //获得兄弟节点
if (node != sibling) { /* node == parent->rb_left */ // node 是左节点
if (rb_is_red(sibling)) { //兄弟节点是红色
/* // 左旋兄弟节点 + 此时就是兄弟节点为黑色的处理办法了
* Case 1 - left rotate at parent
*
* P S
* / \ / \
* N s --> p Sr
* / \ / \
* Sl Sr N Sl
*/
tmp1 = sibling->rb_left;
WRITE_ONCE(parent->rb_right, tmp1);
WRITE_ONCE(sibling->rb_left, parent);
rb_set_parent_color(tmp1, parent, RB_BLACK);
__rb_rotate_set_parents(parent, sibling, root,
RB_RED);
augment_rotate(parent, sibling);
sibling = tmp1;
}
//兄弟节点为黑色
tmp1 = sibling->rb_right; //获取兄弟节点的右节点
if (!tmp1 || rb_is_black(tmp1)) { //右节点为空或右节点为黑
tmp2 = sibling->rb_left; //获取兄弟节点的left节点
if (!tmp2 || rb_is_black(tmp2)) {//left节点为空或left节点为黑
/*
* Case 2 - sibling color flip
* (p could be either color here)
*
* (p) (p)
* / \ / \
* N S --> N s
* / \ / \
* Sl Sr Sl Sr
*
* This leaves us violating 5) which
* can be fixed by flipping p to black
* if it was red, or by recursing at p.
* p is red when coming from Case 1.
*/
rb_set_parent_color(sibling, parent,
RB_RED);
// 兄弟节点变红,如果父亲节点是红色就变黑
if (rb_is_red(parent))
rb_set_black(parent);
else { //否则向上递归,已parent为新node
node = parent;
parent = rb_parent(node);
if (parent)
continue;
}
break;
}
//left节点为红色,兄弟节点右旋,父亲节点左旋,父亲节点变为黑色
/*
* Case 3 - right rotate at sibling
* (p could be either color here)
*
* (p) (p)
* / \ / \
* N S --> N sl
* / \ \
* sl Sr S
* \
* Sr
*
* Note: p might be red, and then both
* p and sl are red after rotation(which
* breaks property 4). This is fixed in
* Case 4 (in __rb_rotate_set_parents()
* which set sl the color of p
* and set p RB_BLACK)
*
* (p) (sl)
* / \ / \
* N sl --> P S
* \ / \
* S N Sr
* \
* Sr
*/
tmp1 = tmp2->rb_right;
WRITE_ONCE(sibling->rb_left, tmp1);
WRITE_ONCE(tmp2->rb_right, sibling);
WRITE_ONCE(parent->rb_right, tmp2);
if (tmp1)
rb_set_parent_color(tmp1, sibling,
RB_BLACK);
augment_rotate(sibling, tmp2);
tmp1 = sibling;
sibling = tmp2;
}
// 此时就相当于右子节点为红色了,左节点也为红色,是无所谓的,右边节点旋转一次更快,兄弟节点肯定为红色
/*
* Case 4 - left rotate at parent + color flips
* (p and sl could be either color here.
* After rotation, p becomes black, s acquires
* p's color, and sl keeps its color)
*
* (p) (s)
* / \ / \
* N S --> P Sr
* / \ / \
* (sl) sr N (sl)
*/
tmp2 = sibling->rb_left;
WRITE_ONCE(parent->rb_right, tmp2);
WRITE_ONCE(sibling->rb_left, parent);
rb_set_parent_color(tmp1, sibling, RB_BLACK);
if (tmp2)
rb_set_parent(tmp2, parent);
__rb_rotate_set_parents(parent, sibling, root,
RB_BLACK);
augment_rotate(parent, sibling);
break;
} else { // 兄弟节点在左边
sibling = parent->rb_left;
if (rb_is_red(sibling)) {
/* Case 1 - right rotate at parent */
tmp1 = sibling->rb_right;
WRITE_ONCE(parent->rb_left, tmp1);
WRITE_ONCE(sibling->rb_right, parent);
rb_set_parent_color(tmp1, parent, RB_BLACK);
__rb_rotate_set_parents(parent, sibling, root,
RB_RED);
augment_rotate(parent, sibling);
sibling = tmp1;
}
tmp1 = sibling->rb_left;
if (!tmp1 || rb_is_black(tmp1)) {
tmp2 = sibling->rb_right;
if (!tmp2 || rb_is_black(tmp2)) {
/* Case 2 - sibling color flip */
rb_set_parent_color(sibling, parent,
RB_RED);
if (rb_is_red(parent))
rb_set_black(parent);
else {
node = parent;
parent = rb_parent(node);
if (parent)
continue;
}
break;
}
/* Case 3 - left rotate at sibling */
tmp1 = tmp2->rb_left;
WRITE_ONCE(sibling->rb_right, tmp1);
WRITE_ONCE(tmp2->rb_left, sibling);
WRITE_ONCE(parent->rb_left, tmp2);
if (tmp1)
rb_set_parent_color(tmp1, sibling,
RB_BLACK);
augment_rotate(sibling, tmp2);
tmp1 = sibling;
sibling = tmp2;
}
/* Case 4 - right rotate at parent + color flips */
tmp2 = sibling->rb_right;
WRITE_ONCE(parent->rb_left, tmp2);
WRITE_ONCE(sibling->rb_right, parent);
rb_set_parent_color(tmp1, sibling, RB_BLACK);
if (tmp2)
rb_set_parent(tmp2, parent);
__rb_rotate_set_parents(parent, sibling, root,
RB_BLACK);
augment_rotate(parent, sibling);
break;
}
}
}
/* Non-inline version for rb_erase_augmented() use */
void __rb_erase_color(struct rb_node *parent, struct rb_root *root,
void (*augment_rotate)(struct rb_node *old, struct rb_node *new))
{
____rb_erase_color(parent, root, augment_rotate);
}
EXPORT_SYMBOL(__rb_erase_color);
/*
* Non-augmented rbtree manipulation functions.
*
* We use dummy augmented callbacks here, and have the compiler optimize them
* out of the rb_insert_color() and rb_erase() function definitions.
*/
static inline void dummy_propagate(struct rb_node *node, struct rb_node *stop) {}
static inline void dummy_copy(struct rb_node *old, struct rb_node *new) {}
static inline void dummy_rotate(struct rb_node *old, struct rb_node *new) {}
static const struct rb_augment_callbacks dummy_callbacks = {
.propagate = dummy_propagate,
.copy = dummy_copy,
.rotate = dummy_rotate
};
void rb_insert_color(struct rb_node *node, struct rb_root *root)
{
__rb_insert(node, root, dummy_rotate);
}
EXPORT_SYMBOL(rb_insert_color);
void rb_erase(struct rb_node *node, struct rb_root *root)
{
struct rb_node *rebalance;
rebalance = __rb_erase_augmented(node, root, &dummy_callbacks);
if (rebalance)
____rb_erase_color(rebalance, root, dummy_rotate);
}
EXPORT_SYMBOL(rb_erase);
/*
* Augmented rbtree manipulation functions.
*
* This instantiates the same __always_inline functions as in the non-augmented
* case, but this time with user-defined callbacks.
*/
void __rb_insert_augmented(struct rb_node *node, struct rb_root *root,
void (*augment_rotate)(struct rb_node *old, struct rb_node *new))
{
__rb_insert(node, root, augment_rotate);
}
EXPORT_SYMBOL(__rb_insert_augmented);
/*
* This function returns the first node (in sort order) of the tree.
*/
struct rb_node *rb_first(const struct rb_root *root)
{
struct rb_node *n;
n = root->rb_node;
if (!n)
return NULL;
while (n->rb_left)
n = n->rb_left;
return n;
}
EXPORT_SYMBOL(rb_first);
struct rb_node *rb_last(const struct rb_root *root)
{
struct rb_node *n;
n = root->rb_node;
if (!n)
return NULL;
while (n->rb_right)
n = n->rb_right;
return n;
}
EXPORT_SYMBOL(rb_last);
struct rb_node *rb_next(const struct rb_node *node)
{
struct rb_node *parent;
if (RB_EMPTY_NODE(node))
return NULL;
/*
* If we have a right-hand child, go down and then left as far
* as we can.
*/
if (node->rb_right) {
node = node->rb_right;
while (node->rb_left)
node = node->rb_left;
return (struct rb_node *)node;
}
/*
* No right-hand children. Everything down and left is smaller than us,
* so any 'next' node must be in the general direction of our parent.
* Go up the tree; any time the ancestor is a right-hand child of its
* parent, keep going up. First time it's a left-hand child of its
* parent, said parent is our 'next' node.
*/
while ((parent = rb_parent(node)) && node == parent->rb_right)
node = parent;
return parent;
}
EXPORT_SYMBOL(rb_next);
struct rb_node *rb_prev(const struct rb_node *node)
{
struct rb_node *parent;
if (RB_EMPTY_NODE(node))
return NULL;
/*
* If we have a left-hand child, go down and then right as far
* as we can.
*/
if (node->rb_left) {
node = node->rb_left;
while (node->rb_right)
node = node->rb_right;
return (struct rb_node *)node;
}
/*
* No left-hand children. Go up till we find an ancestor which
* is a right-hand child of its parent.
*/
while ((parent = rb_parent(node)) && node == parent->rb_left)
node = parent;
return parent;
}
EXPORT_SYMBOL(rb_prev);
void rb_replace_node(struct rb_node *victim, struct rb_node *new,
struct rb_root *root)
{
struct rb_node *parent = rb_parent(victim);
/* Copy the pointers/colour from the victim to the replacement */
*new = *victim;
/* Set the surrounding nodes to point to the replacement */
if (victim->rb_left)
rb_set_parent(victim->rb_left, new);
if (victim->rb_right)
rb_set_parent(victim->rb_right, new);
__rb_change_child(victim, new, parent, root);
}
EXPORT_SYMBOL(rb_replace_node);
void rb_replace_node_rcu(struct rb_node *victim, struct rb_node *new,
struct rb_root *root)
{
struct rb_node *parent = rb_parent(victim);
/* Copy the pointers/colour from the victim to the replacement */
*new = *victim;
/* Set the surrounding nodes to point to the replacement */
if (victim->rb_left)
rb_set_parent(victim->rb_left, new);
if (victim->rb_right)
rb_set_parent(victim->rb_right, new);
/* Set the parent's pointer to the new node last after an RCU barrier
* so that the pointers onwards are seen to be set correctly when doing
* an RCU walk over the tree.
*/
__rb_change_child_rcu(victim, new, parent, root);
}
EXPORT_SYMBOL(rb_replace_node_rcu);
static struct rb_node *rb_left_deepest_node(const struct rb_node *node)
{
for (;;) {
if (node->rb_left)
node = node->rb_left;
else if (node->rb_right)
node = node->rb_right;
else
return (struct rb_node *)node;
}
}
struct rb_node *rb_next_postorder(const struct rb_node *node)
{
const struct rb_node *parent;
if (!node)
return NULL;
parent = rb_parent(node);
/* If we're sitting on node, we've already seen our children */
if (parent && node == parent->rb_left && parent->rb_right) {
/* If we are the parent's left node, go to the parent's right
* node then all the way down to the left */
return rb_left_deepest_node(parent->rb_right);
} else
/* Otherwise we are the parent's right node, and the parent
* should be next */
return (struct rb_node *)parent;
}
EXPORT_SYMBOL(rb_next_postorder);
struct rb_node *rb_first_postorder(const struct rb_root *root)
{
if (!root->rb_node)
return NULL;
return rb_left_deepest_node(root->rb_node);
}
EXPORT_SYMBOL(rb_first_postorder);
版权声明:本文为weixin_44708624原创文章,遵循 CC 4.0 BY-SA 版权协议,转载请附上原文出处链接和本声明。