词法分析
词法分析的任务
字符流到记号流
-
字符流:
- 和被编译的语言密切相关(ASCII, Unicode, or …)
-
记号流:
- 编译器内部定义的数据结构,编码所识别出的词法单元
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-A1TcpRn7-1629003388273)(https://i.bmp.ovh/imgs/2020/09/f35759edf271af84.png)]
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-8ikLBZin-1629003388275)(https://i.bmp.ovh/imgs/2020/09/74017cb7ba8fcd04.png)]
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-La6WeT3f-1629003388276)(https://i.bmp.ovh/imgs/2020/09/3d619125d4e36e47.png)]
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Kfjyskor-1629003388279)(https://i.bmp.ovh/imgs/2020/09/a42e5578aa5e0db1.png)]
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-huDypTwN-1629003388281)(https://i.bmp.ovh/imgs/2020/09/9ec263bed47ae85b.png)]
记号的数据结构定义
enum kind {IF, LPAREN, ID, INTLIT, ...};
struct token {
enum kind k;
char *lexeme;
};
词法分析器–手工构造法
至少两种实现方案:
-
手工编码实现法
- 相对复杂、且容易出错
-
但是目前非常流行的实现方法
- GCC, LLVM, …
-
词法分析器的生成器
- 可快速原型、代码量较少
- 但较难控制细节
转移图
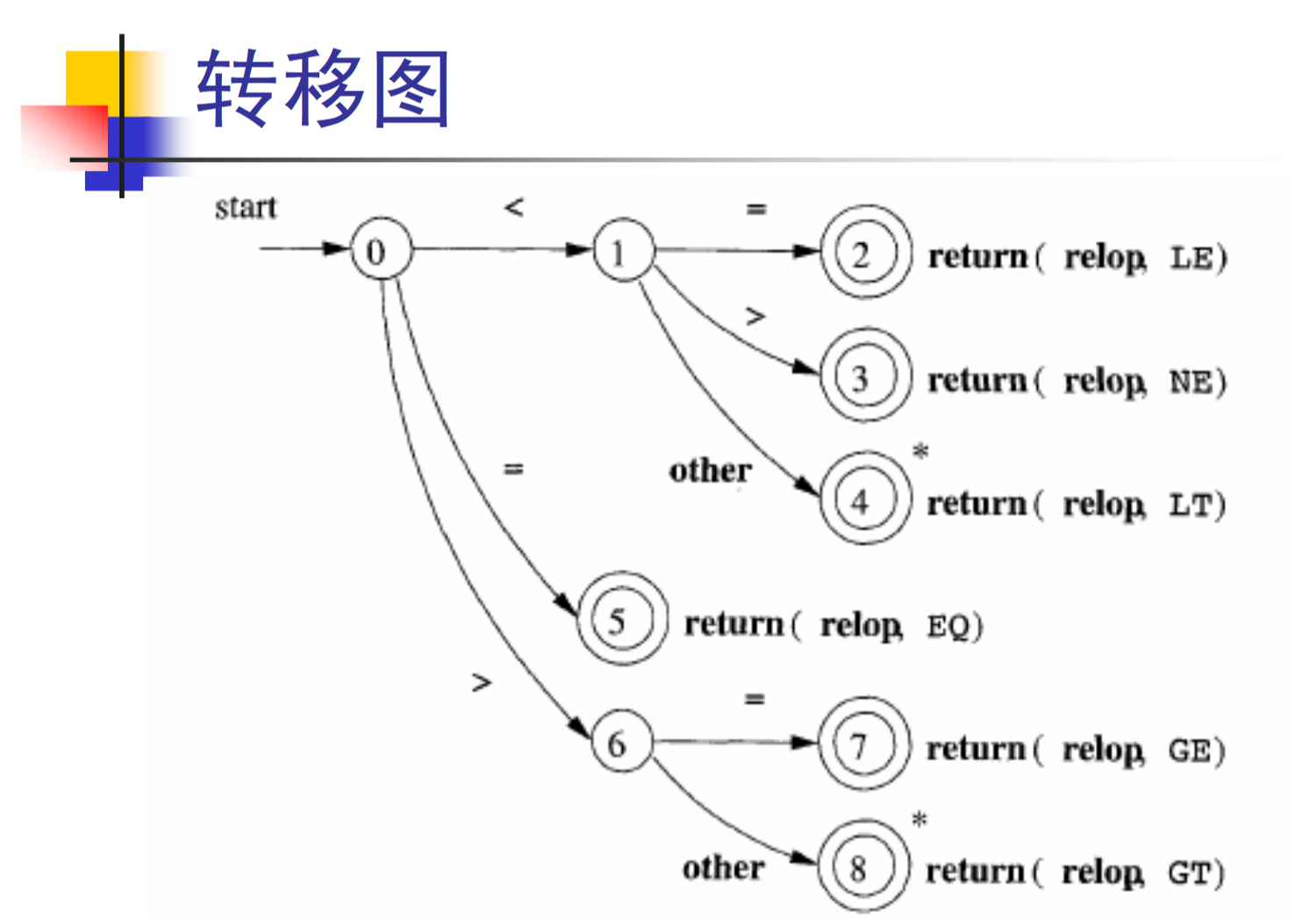
token nextToken()
c = getChar();
switch (c)
case '<':
c = getChar();
switch (c)
case '=': return LE;
case '>': return NE;
default: rollback(); return LT;
case '=': return EQ;
case '>':
c = getChar();
switch (c): // similar
标识符的转移图
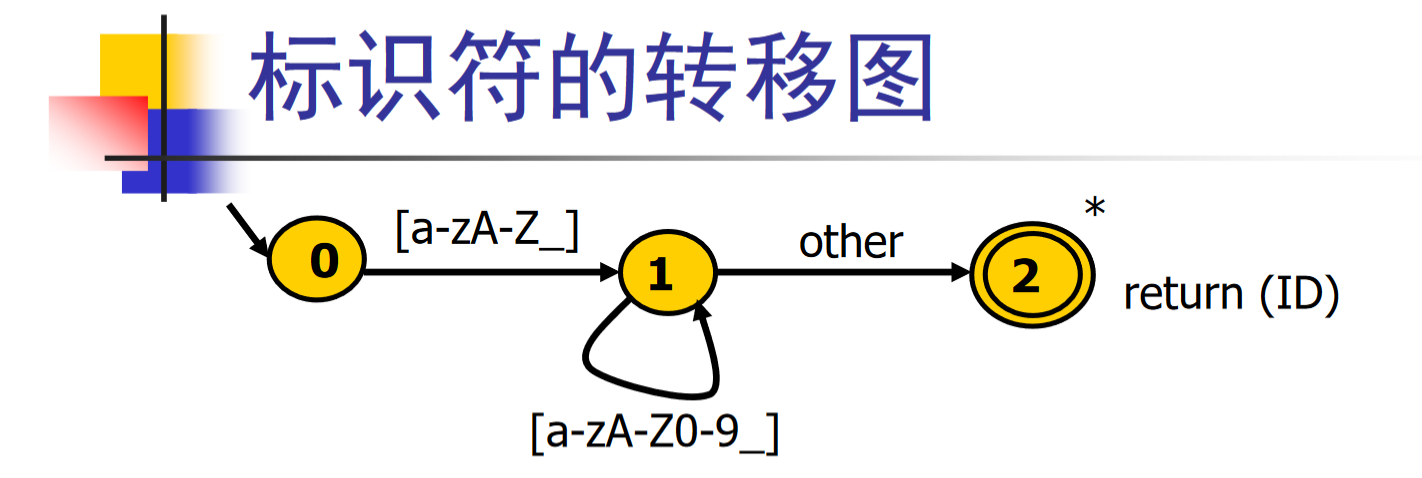
token nextToken()
c = getChar();
switch (c)
// continued from above cases...
case 'a', ..., 'z', 'A', ..., 'Z', '_':
c = getChar();
while (c == 'a' || c == 'b' || ... || c == '_')
c = getChar();
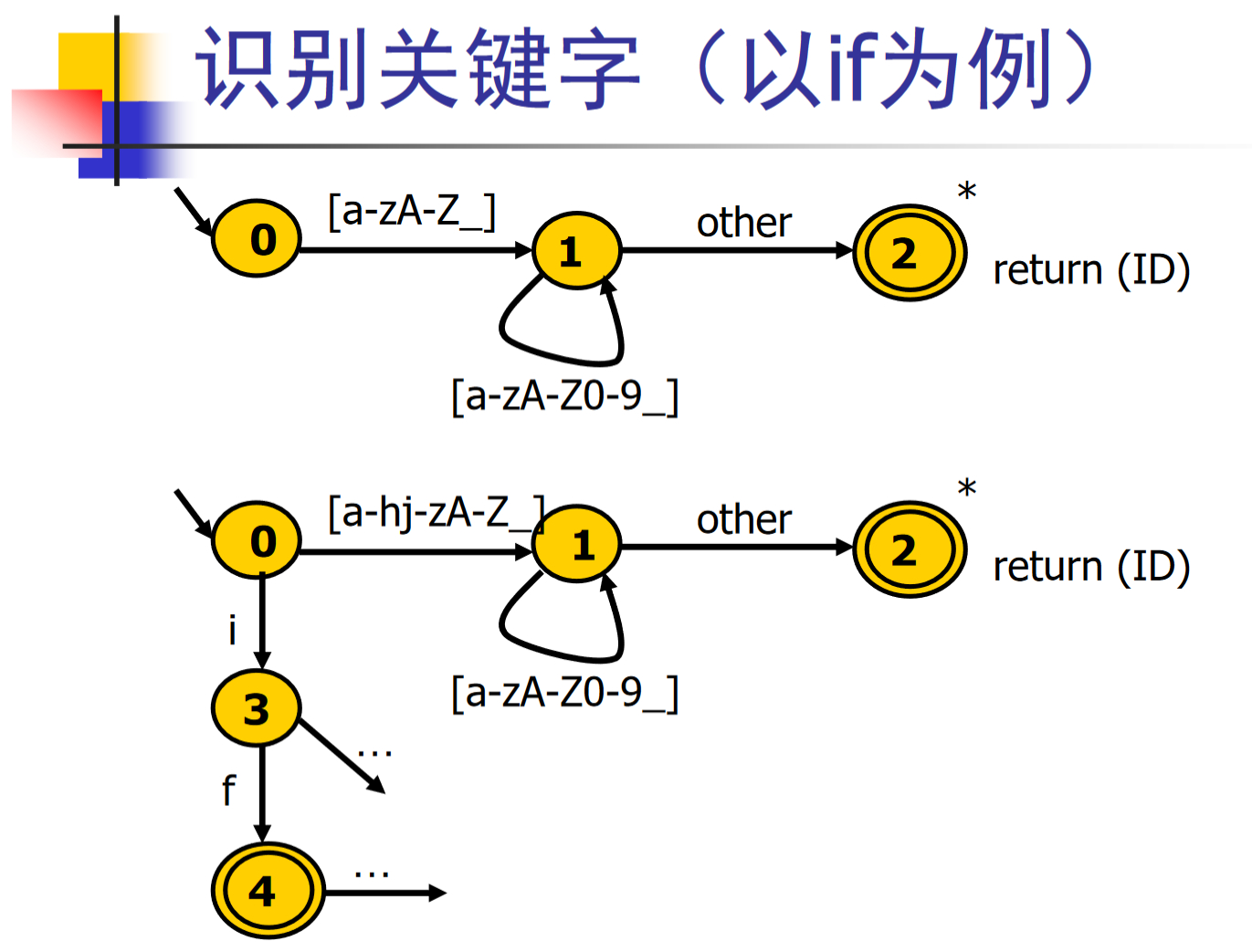
标识符和关键字
-
很多语言中的标识符和关键字有交集
- 从词法分析的角度看,关键字是标识符的一部分
-
以C语言为例:
- 标识符:以字母或下划线开头,后跟零个或多个字母、下划线、或数字
- 关键字:if, while, else, …
关键字表算法
- 对给定语言中所有的关键字,构造关键字构成的哈希表H
- 对所有的标识符和关键字,先统一按标识符的转移图进行识别
- 识别完成后,进一步查表H看是否是关键字
-
通过合理的构造哈希表H(
完美哈希
),可以O(1)时间完成
正则表达式
- 对给定的字符集∑={c1, c2, …, cn}
-
归纳定义:
- 空串ε是正则表达式
- 对于任意c∈∑,c是正则表达式
-
如果M和N是正则表达式, 则以下也是正则表达式
- 选择 M | N = {M, N}
- 连接 MN = {mn | m∈M, n∈N}
- 闭包 M* = {ε, M, MM, MMM, …}

语法糖
-
可以引入更多的语法糖,来简化构造
- [c1-cn] == c1|c2|…|cn
- e+ == 一个或多个e
- e? == 零个或一个e
- “a*” == a* 自身, 不是a的Kleen闭包
- e{i, j} == i到j个e的连接
- . == 除‘\n’外的任意字符
有限状态自动机
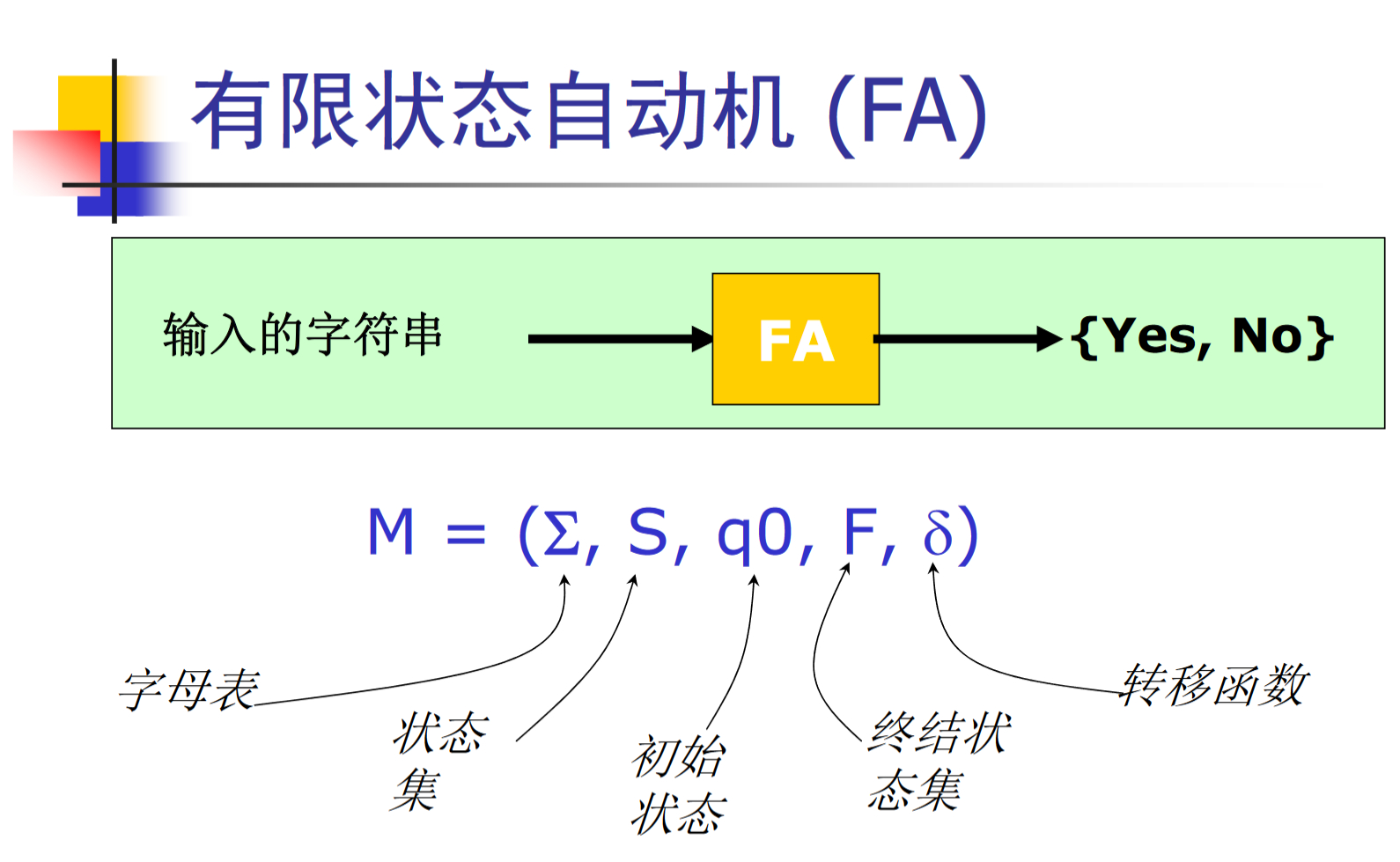
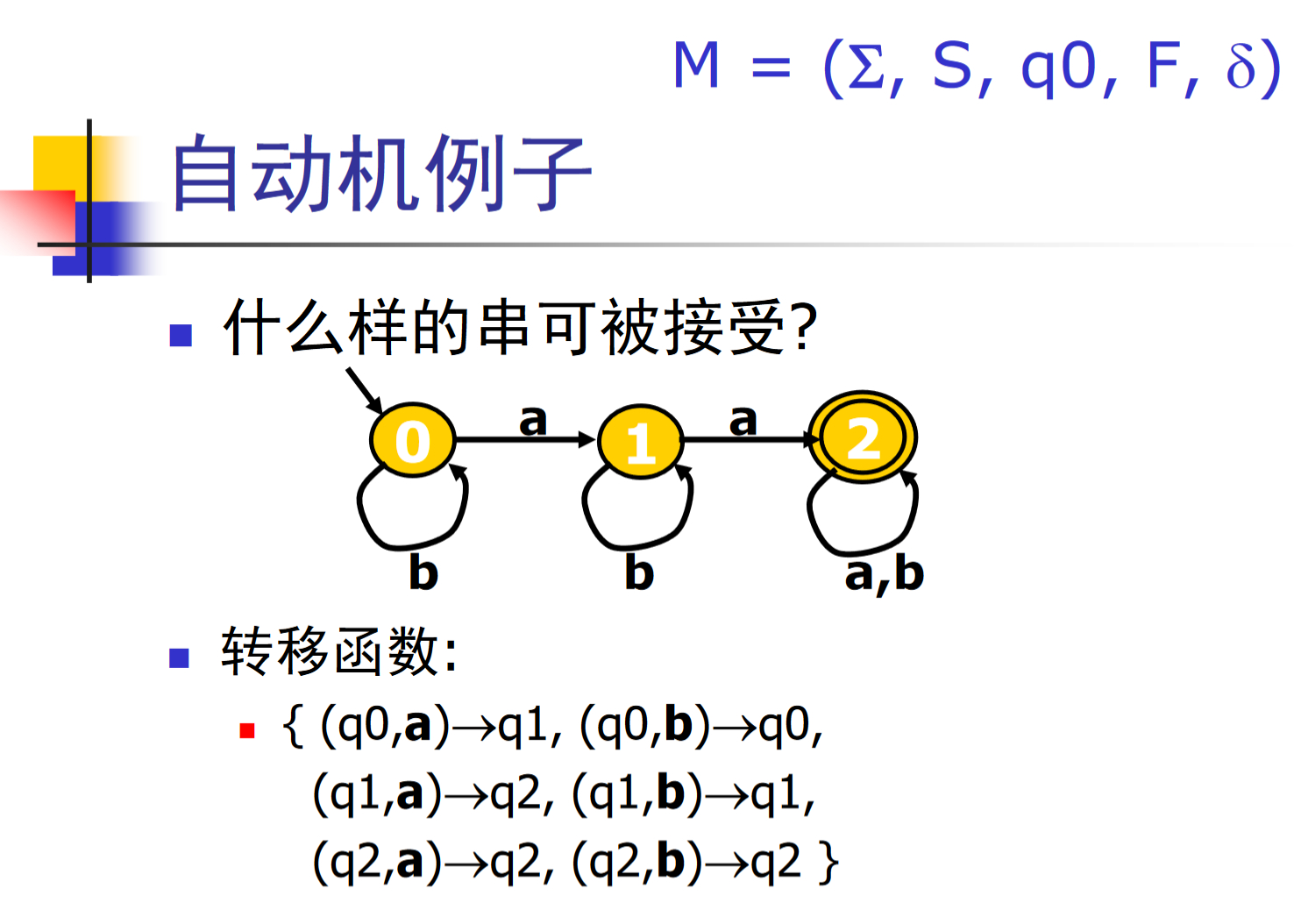
-
确定状态有限自动机DFA
-
对任意的字符,最多有一个状态可以转移
- δ: S x Σ → S
-
对任意的字符,最多有一个状态可以转移
-
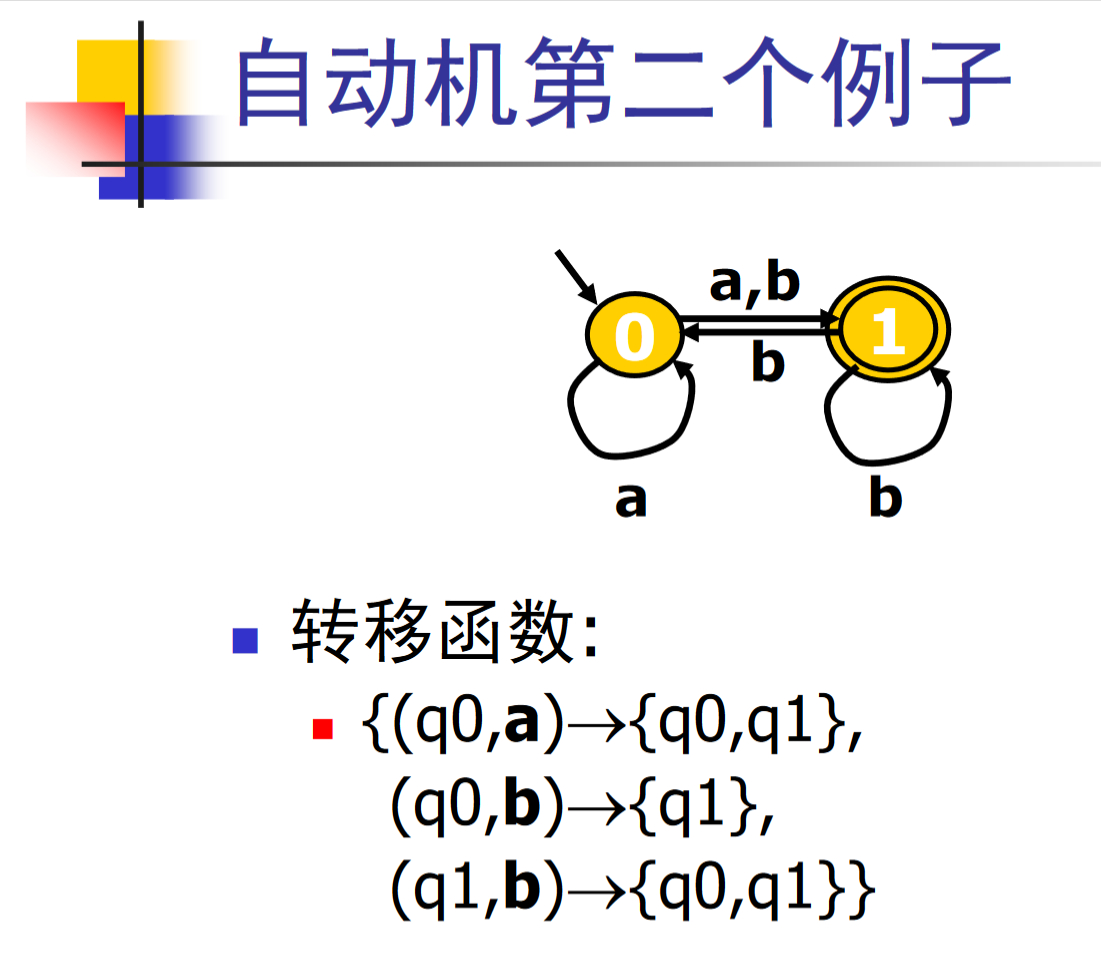
非确定的有限状态自动机NFA
-
对任意的字符,有多于一个状态可以转移
- δ: S x (Σ∪ε) → 2^S (幂集)
-
对任意的字符,有多于一个状态可以转移
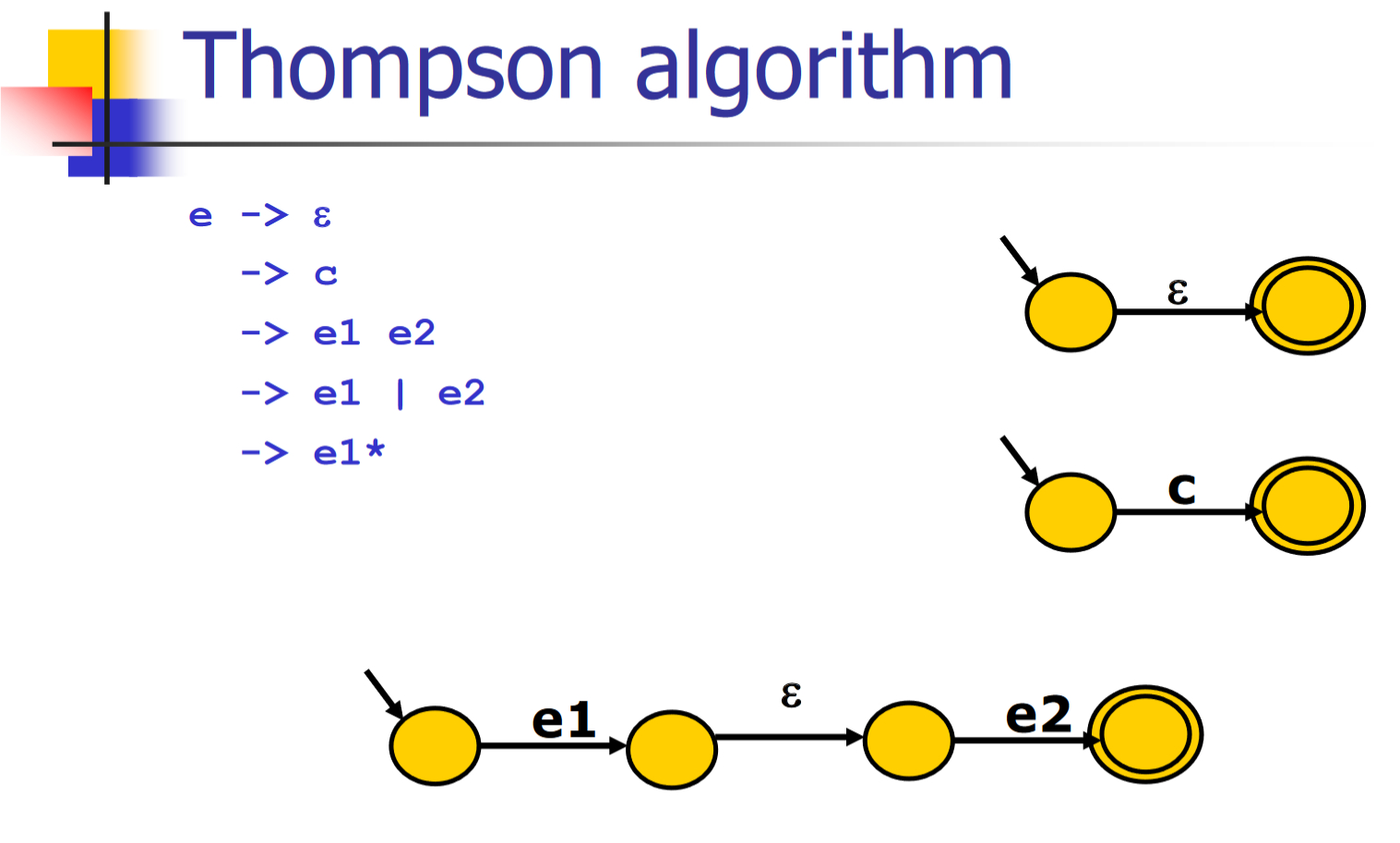
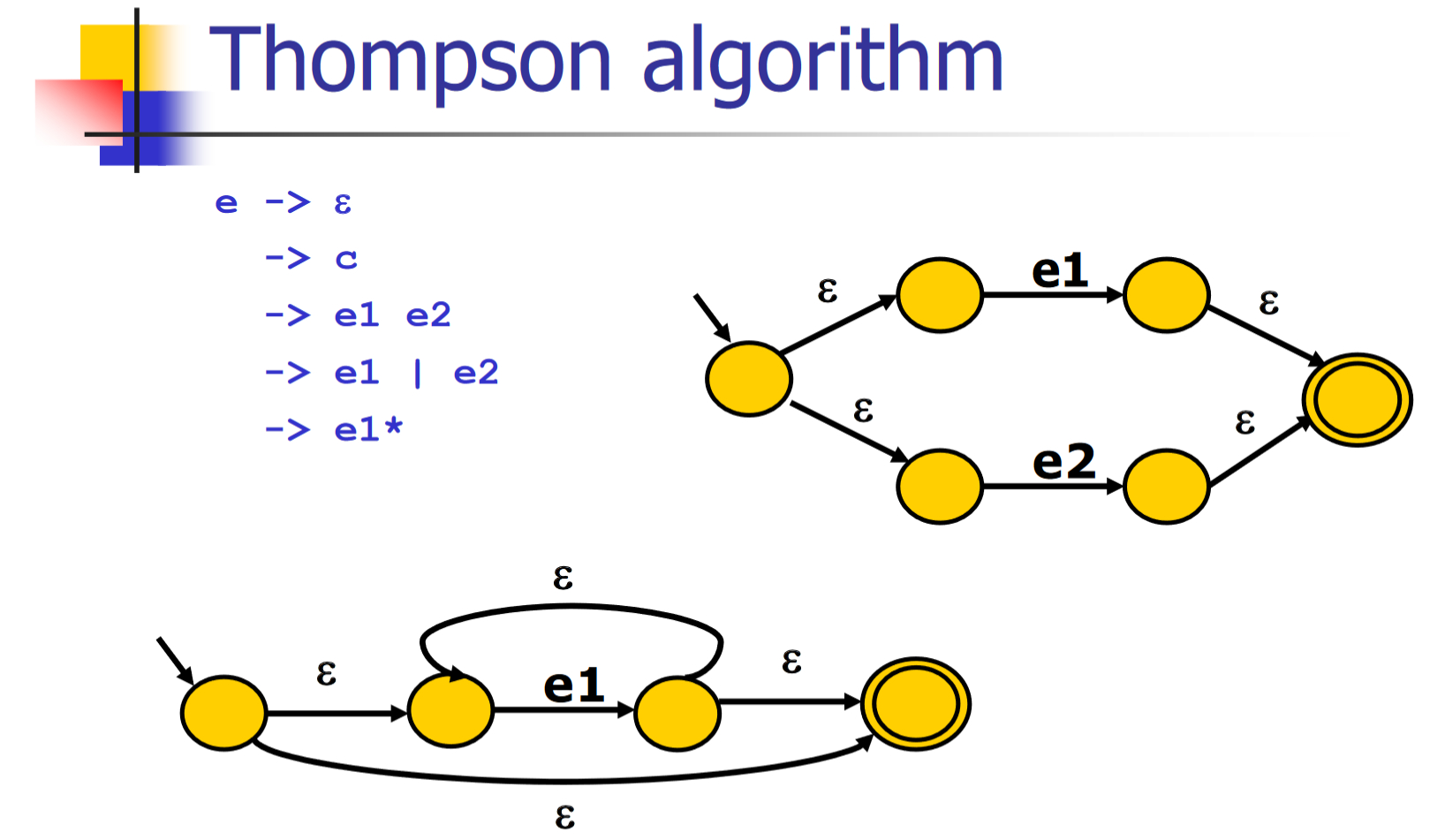
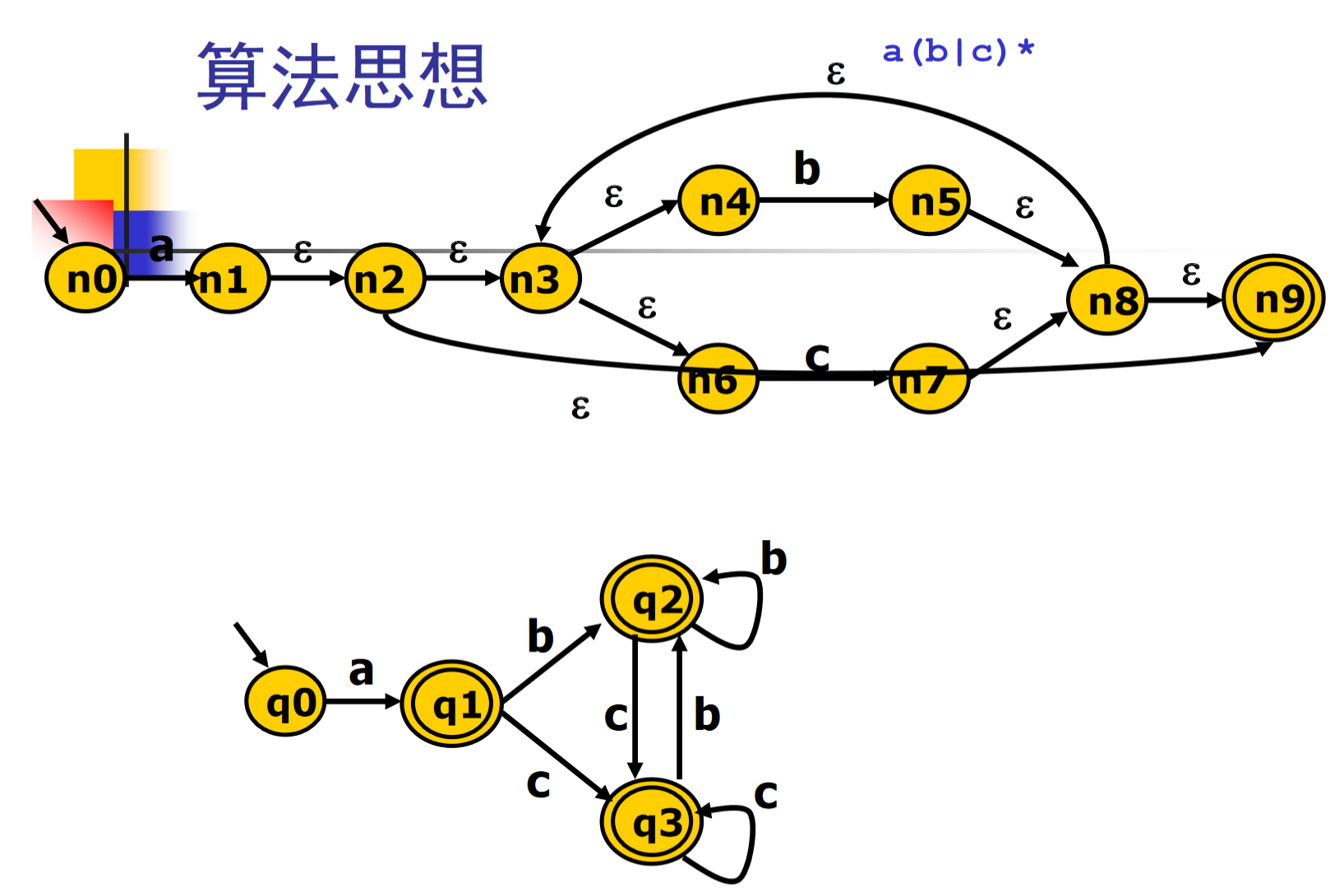
正则表达式到非确定有限状态自动机
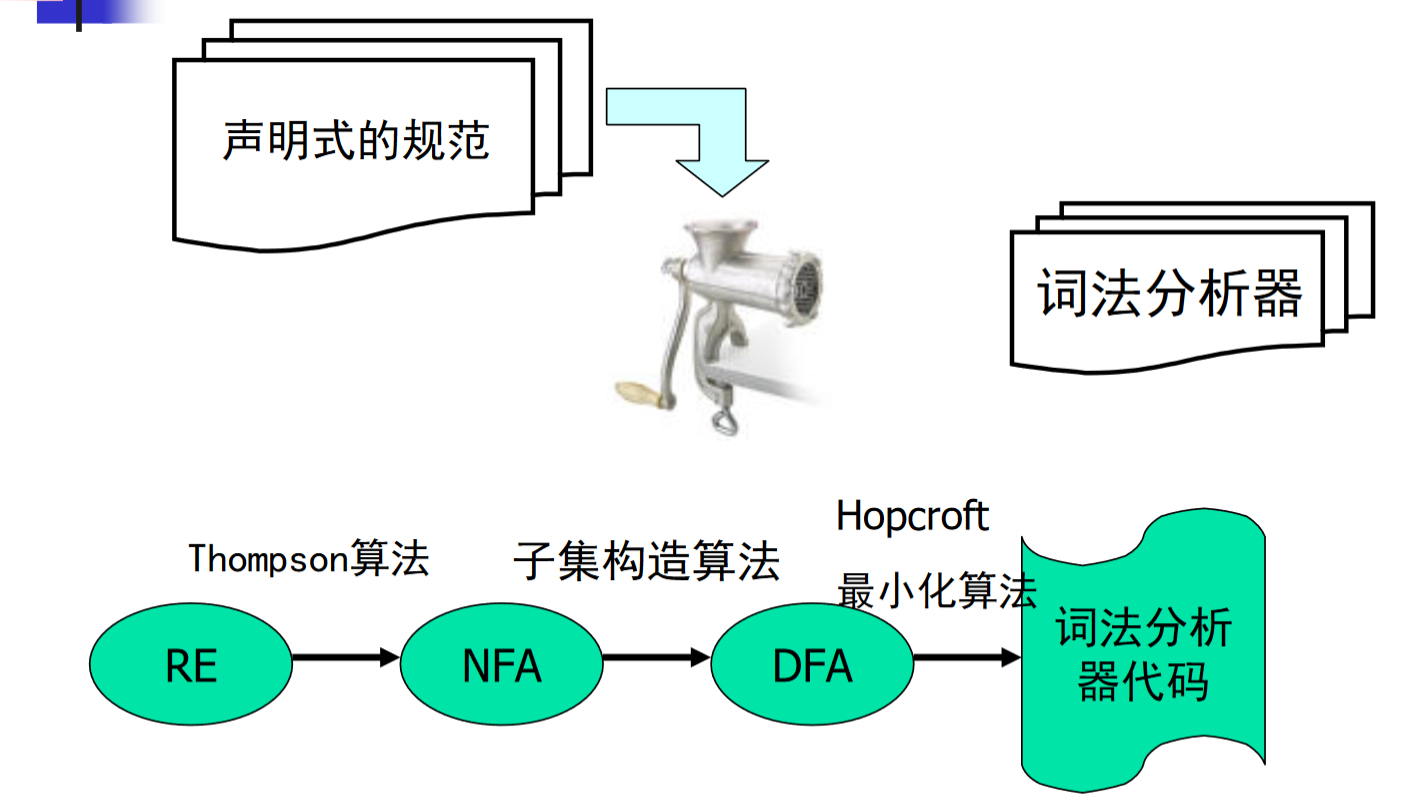
Thompson 算法
-
基于对RE的结构做归纳
- 对基本的RE直接构造
- 对复合的RE递归构造
- 递归算法,容易实现
NFA 到 DFA
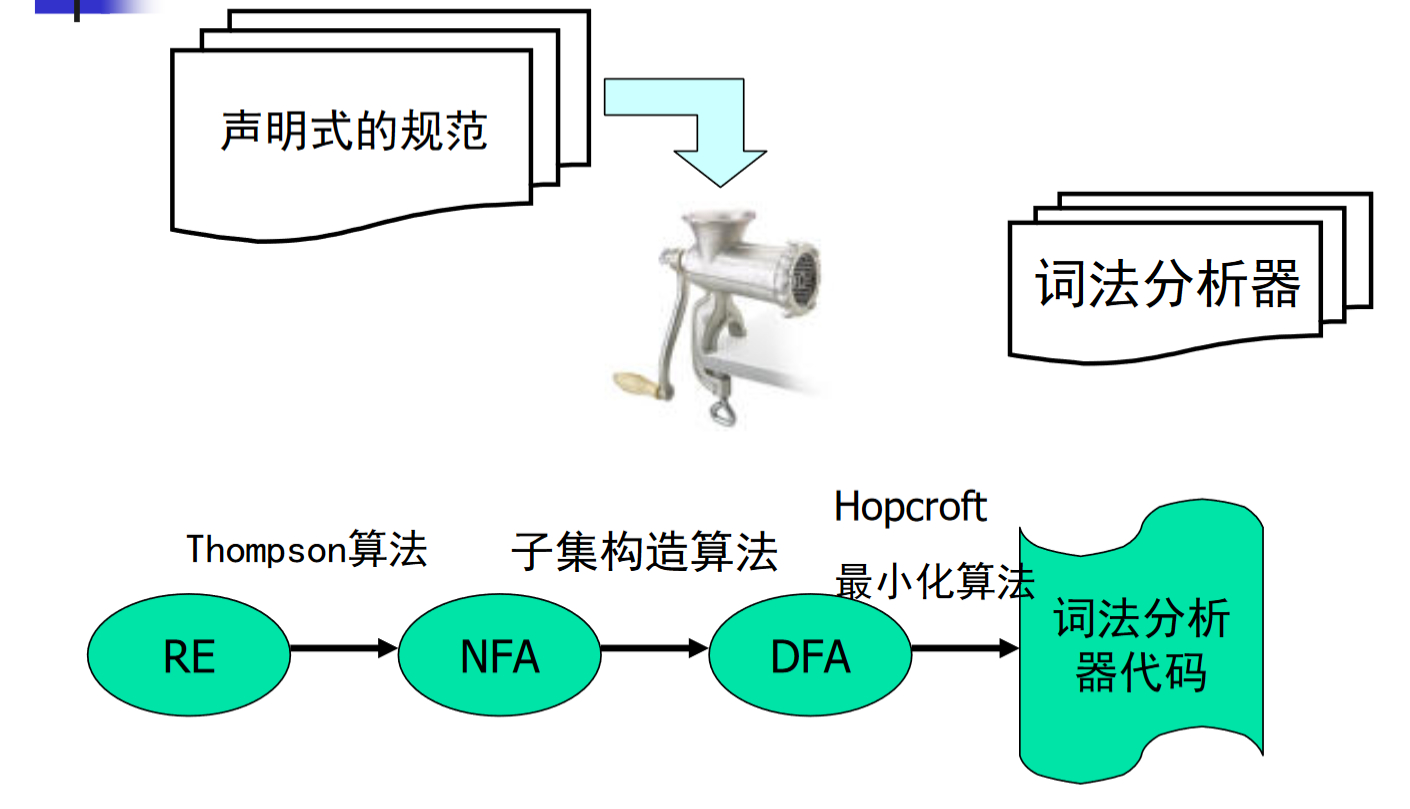
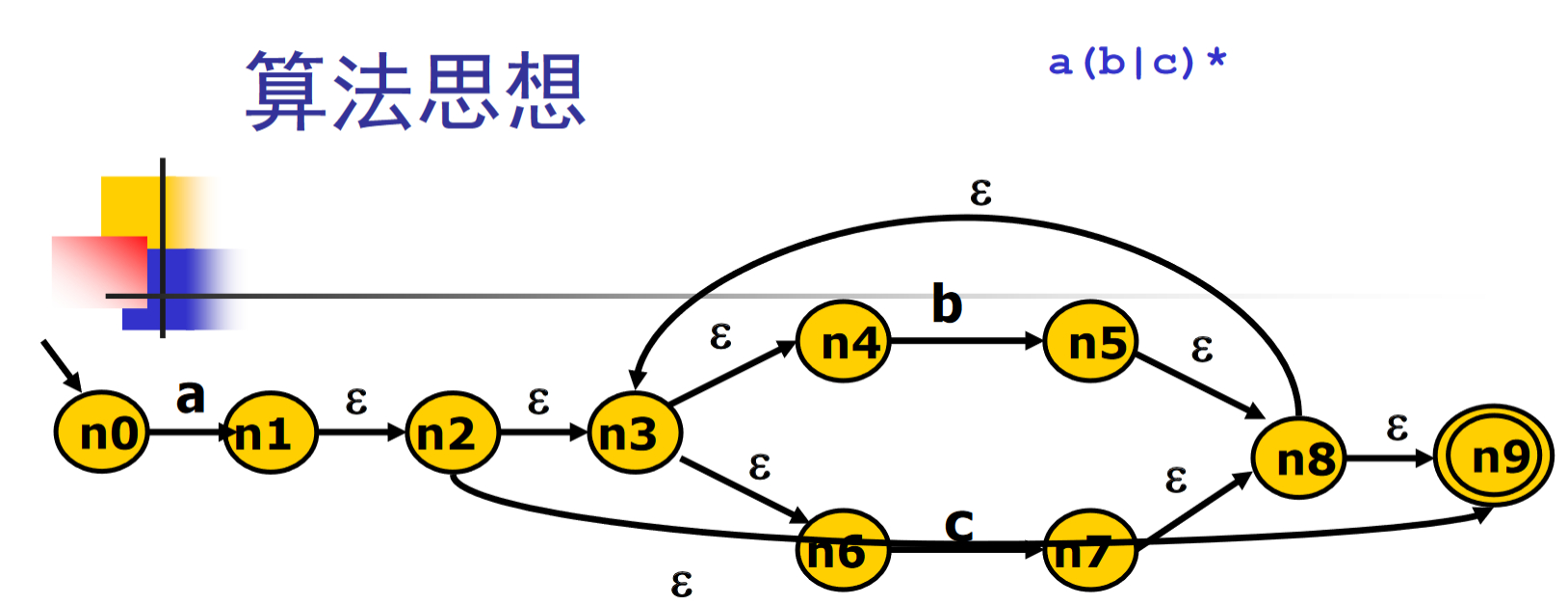
子集构造算法
/* 子集构造算法:工作表算法 */
q0 <- eps_closure(n0)
Q <- { q0 }
workList <- q0
while (workList != [])
remove q from workList
foreach (character c)
t <- eps_closure(delta(q, c))
D[q, c] <- t
if (t \not\in Q)
add t to Q and workList
对算法的讨论
-
不动点算法
- 算法为什么能够运行终止
-
时间复杂度
- 最坏情况 O(2N)
-
但在实际中不常发生
- 因为并不是每个子集都会出现
ε 的闭包运算
深度优先
/* 基于深度优先遍历的算法 */
set closure = {};
void eps_closure (x)
closure += {x}
foreach (y : x -- ε --> y)
if(!visited(y))
eps_closure (y)
广度优先
/* 基于广度优先的算法 */
set closure = {};
Q = []; // queue
void eps_closure(x)
Q = [x];
while (Q not empty)
q <- deQueue (Q)
closure += q
foreach (y : q -- ε --> y)
if (!visited(y))
enQueue(Q, y)
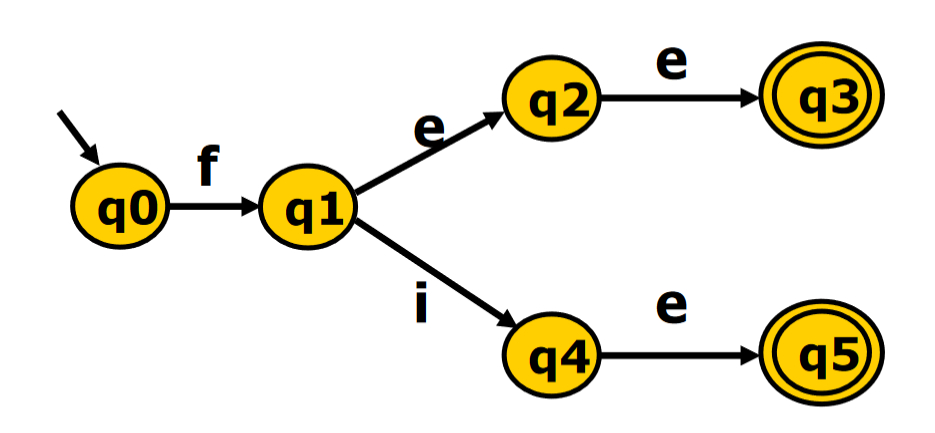
DFA 的最小化
Hopcroft 算法
// 基于等价类的思想
split(S)
foreach (character c)
if (c can split S)
split S into T1, ..., Tk
hopcroft()
split all nodes into N, A
while (set is still changes)
split(S)

算法的讨论
-
不动点算法
- 算法为什么能够运行终止
-
时间复杂度
- 最坏情况O(2N)?
-
实际中运行可能会更快
- 因为并不是每个子集都会分裂
DFA 的代码表示
- 概念上讲, DFA是一个有向图
-
实际上,有不同的DFA的代码表示
- 转移表(类似于邻接矩阵)
- 哈希表
- 跳转表
- 取决于在实际实现中,对时间空间的权衡
转移表
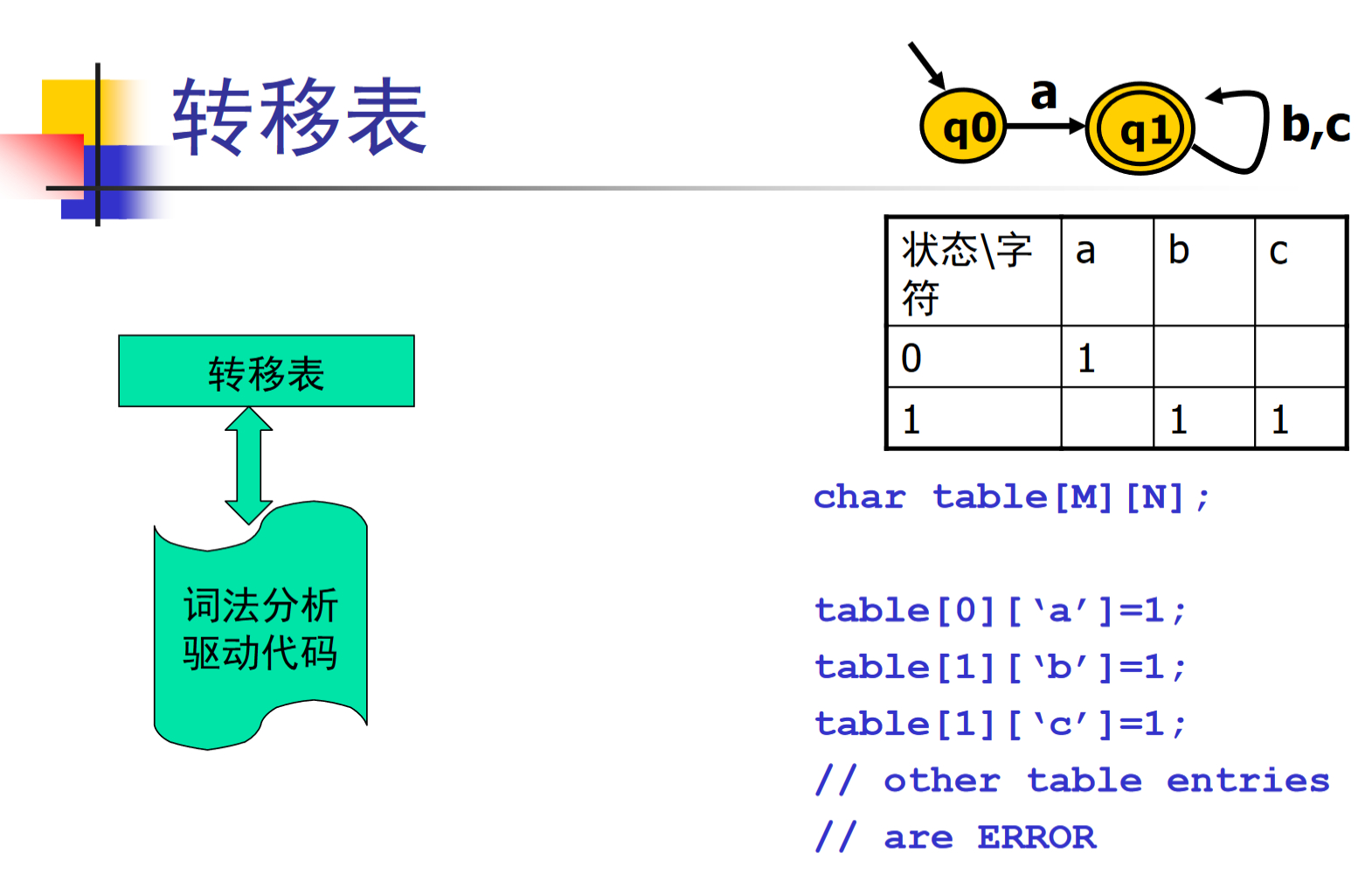
驱动代码
nextToken()
state = 0
stack = []
while (state != ERROR)
c = getChar()
if (state is ACCEPT)
clear(stack)
push(state)
state = table[state][c]
while (state is not ACCEPT)
state = pop()
rollback()

跳转表
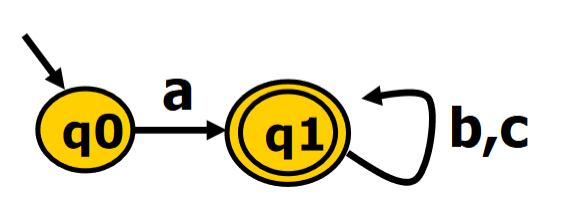
nextToken()
state = 0
stack = []
goto q0
q0:
c = getChar()
if (state is ACCEPT)
clear(stack)
push(state)
if(c == 'a')
goto q1
q1:
c = getChar()
if (state is ACCEPT)
clear(stack)
push(state)
if (c == 'b' || c == 'c')
goto q1