DFS 树

翻译自

THe DFS tree and its applications: how I found out I really didn’t understand bridges

介绍

这是一篇对可以用图的 DFS 树来解的题的教程/扩展。

在很长一段时间，我并没有真正理解传统算法是如何找到桥的。很多题解看起来没有真正解释它是如何工作的，很多只是顺带提到它但后迅速地进入实现部分。某一天有人解释了 DFS 树是什么，我才终于正确地理解了它。在此之前，我花了很长时间去理解寻找桥的算法，而且我经常要注意一些细节。现在我已经可以用打字的速度去实现它了。

但是更重要的是，我开始明白同样的算法该如何用在与桥或多或少无关的题目上。这件事，就像当你有一个黑盒时，你只可以把它当作一个黑盒去使用。但如果你有一个你十分了解的盒子，你可以把它分解，略加改动并把啊用在完全不同的事情上，并且毫无疏漏。

就我而言，DFS 树是我所知的解决图的结构问题最好的算法之一。此外，有时在你使用 DFS 树后，一些可疑的贪心算法的正确性也会变得显而易见。

考虑一个无向连通图 G，对它进行深度优先遍历。它可以用一个递归函数来实现，就像这样：

function visit(u):
     mark u as visited
     for each vertex v among the neighbours of u:
         if v is not visited:
             mark the edge uv
             call visit(v)

以下是实现过程的动画：

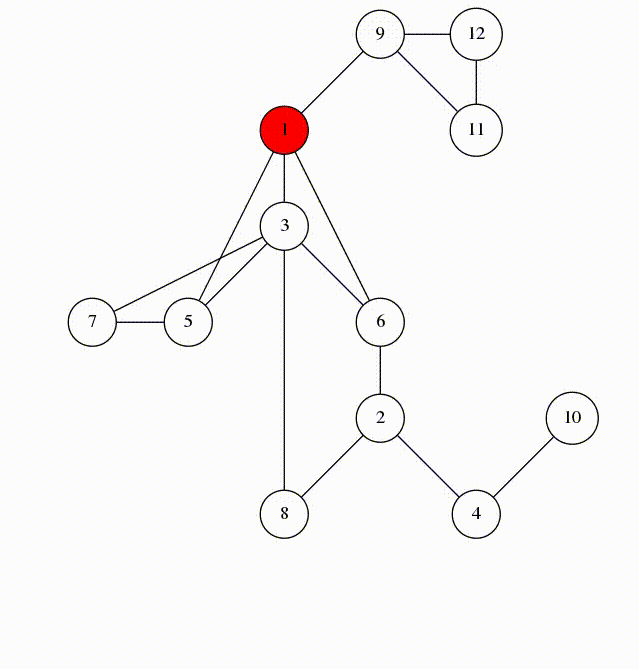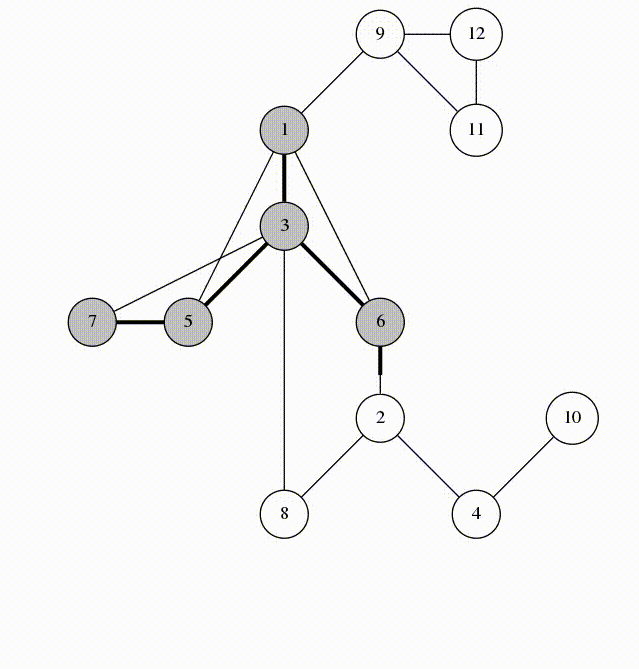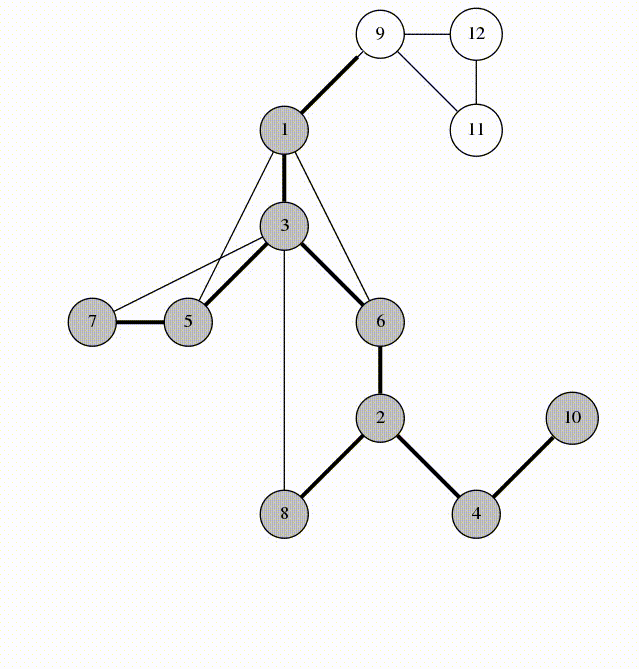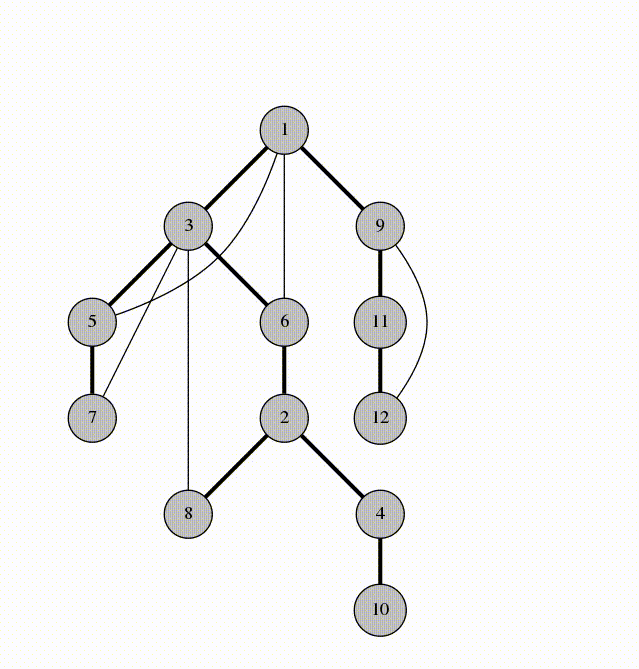
在这里插入图片描述

我们看一下在第 5 行被标记的边。他们构成 G 的以 1 为根的生成树。我们称这些边为

树边

，其他的所有边为

回边

。

这就是我们图的 DFS 树：

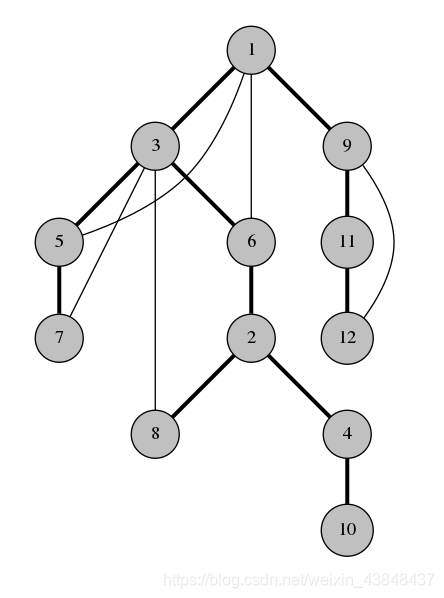
在这里插入图片描述

结论 1

：在生成树种，图的回边连接的都是一个顶点和它的子孙节点。

这就是 DFS 树好用的原因

。

证明：假设有一条边 uv，深度优先遍历已经访问了 u 但还没访问到 v。然后：

\cdot

$\cdot$

如果深度优先遍历沿着 uv 边由 u 走向 v，那么 uv 是一条树边。

\cdot

$\cdot$

如果深度优先遍历没有沿着 uv 从 u 访问 v，然而此时遍历到第四步发现 v 已经被访问过了。说明 v 是在遍历 u 的一个邻居节点时对它进行了访问，这意味着 v 是 u 在 DFS 树中的一个子孙节点。

例如在上面的图中，节点 4 和节点 8

不可能由一条回边相连因为它们各自都不是另一个的祖先节点，如果由一条边连接 4 和 8，遍历会从 4 走向 8 而不是返回 2。

这是 DFS 树最显而易见的结论。DFS 树如此有用因为它简化了图的结构。与其去考虑图中所有种类的边，我们此时只需要考虑一棵树和一些额外的祖先-子孙连边。这样的结构十分适于思考和尝试算法。

找桥（或割点）

DFS 树和结论 1 是 Tarjan 找桥算法的核心。传统的找桥教程只顺带提到了 DFS 树并从定义奇怪的 dfs[u] 数组和 low[u] 数组开始。把这些全部忘掉。这些是实现的细节，在我看来，它们甚至不是实现找桥算法最直观的方法。在找桥算法中，dfs[u] 只是一个用来确认某一顶点是否是 DFS 树中另一顶点的祖先的令人迷惑的方法。同时，也很难清楚地解释 low[u] 代表着什么。

以下就是在一个无向连通图中找桥的方法。考虑图 G 的 DFS 数。

结论 2

：当且仅当树边 uv 不存在连接其祖先和子孙节点的回边时，它是桥。也就是说，树边 uv 是桥当且仅当此时没有回边跨越它。

证明：移出边 uv 将生成书分成了两个互补连接的部分：uv 的子树和剩余的生成树。如果两部分间有回边相连，那么图依旧联通，否则 uv 就是个桥。回边连接这两部分的唯一情况就是它连接了 uv 的祖先和子孙。

例如，在上图的 DFS 树中，连接 6 和 2 的不是桥，因为即使我们移除了它，连接 3 和 8 的回边依旧使图联通。看另一个例子，连接 2 和 4 的边是桥，因为并没有跨越它的回边来使图在移除 2-4 边后继续联通

结论 3

：回边一定不是桥。

这引出了经典的找桥算法。考虑一个图 G:

1.建立这张图的 DFS 树。

2.对每一条树边 uv，寻找是否有一条回边跨越

uv，如果没有，它就是桥。

因为 DFS 树的简单结构，第二步十分容易实现。例如，你可以用传统的 low[u] 方法；或者，可以用前缀和来记录，这就是我推崇的。我用 dp[u] 来定义跨越点 u 和他的父节点的回边的数量。然后：

[

]

dp[u]

$d p [u]$

= (从 u 点开始的向上的回边) – (从 u 点开始向下的回边) +

[

]

是

的

一

个

孩

子

节

点

\sum dp[v] _{v 是 u 的一个孩子节点}

$\sum d p [v]_{v 是 u 的一个孩子节点}$

当且仅当 dp[u] = 0 时连接u及其父节点的边是桥。

给边定向来建立一个强连通图

从这道题开始：

codeforces 118 E – Betown roads

问题 1

：你有一个无向连通图。给每条边定向使生成的有向图是一个强连通图，或者申明这不可能。

我知道一个可以不用 DFS 树思想就能在线性时间解决的方法，但它十分麻烦而且我绝不想实现它。然而，DFS 树的解法仅用几行就可以实现。

结论 4

：如果图 G 有桥，就不可能。

证明：如果 uv 是桥且我们将其定向为 u

\to

$\to$

v，那么现在就不存在由 v 到 u 的边。

现在，假定有一张图不存在桥。让我们观察它的 DFS 树。将所有树边定向向下并将所有回边定向向上。

在这里插入图片描述

结论 5

：根节点可以走到任一节点。

证明：沿着生成书移动即可。

结论 6

：任意节点都可以回到根节点。

证明：考虑一个非根节点 v，假设 u 是它在生成树上的父节点。因为图中没有桥，所以一定存在一条回边跨越 uv，它连接了 v 的一个子孙节点和 u 的一个祖先节点。我们可以从 v 向下走知道到达回边，然后利用他移动到 u 的祖先节点。这样我们至少较之前向根节点上移了一步。重复此操作我们就能到达根节点。

因此，这张图现在已经强联通了。这种方法、可以与用与 DFS 树没有明显关联的方法去实现，但这是一个非常适宜用 DFS 树来证明正确性的例子。

实现仙人掌图

有时候 DFS 树是用来表示图并使实现某一特定事物更简单的方法。就像邻接表，但是比它深一个层次。这一部分单纯是实现的技巧。

仙人掌图是一个所有边（或顶点）至多属于一个简单环的图。第一种情况叫

点仙人掌

，第二种情况叫

边仙人掌

。比起一般的图，仙人掌图由更简单的结构，在仙人掌图上解决问题也比在一般图上更方便。但是在实现时，如果你不思考你在干什么，仙人掌算法的实现将会十分麻烦。

在仙人掌图的 DFS 树中，对于任一条树边，至多有一天回边跨越它。这就将环变成了一一对应的简单环：

\cdot

$\cdot$

每一条回边都与它跨越的树边组成和一个简单环

\cdot

$\cdot$

不存在其他情况的简单环

这样就囊括了仙人掌图大多的特性。因此，可以用这种表示去轻松地实现仙人掌算法。

例如：考虑如下问题：

问题 2

：你有一个联通的有 n 个节点的点仙人掌图。请回答“存在多少个不同的从点 p 到点 q 的简单路径”。

这是

codeforces 231E – Cactus

的大致题意。

官方题解

的方法大致是这样的：

1.将每一个环缩点。然后将这些点标记为黑色；

2.将图定根:

3.对每一个点 u，计算从根节点到 u 的路径上黑色点的个数，记录为 cnt[u]；

4.根据 (p, q) 两点最近公共祖先的颜色判断答案是（白）

[

]

[

]

−

[

(

)

]

2^{cnt[p] + cnt[q] – 2cnt[lca(p, q)]}

$2^{c n t [p] + c n t [q] - 2 c n t [l c a (p, q)]}$

还是（黑）

[

]

[

]

−

[

(

)

]

2^{cnt[p] + cnt[q] – 2cnt[lca(p, q)] + 1}

$2^{c n t [p] + c n t [q] - 2 c n t [l c a (p, q)] + 1}$

这样的方法不难理解。更有意思的部分是它的实现。

在这里插入图片描述

很有效是吧，但是该怎么实现呢？

在一段时间后，大多数人都会找到一些方法去实现它。但这里用 DFS 树会有更简单的方法：

1.给每个回边一个从 N + 1 开始的唯一的编号；

2.对每一个点 u，统计跨越 u 的回边的编号，记为 cycleId[u]；如果 u 不在一个环里，则标记 cycleId[u] = u；

3.建立一个新的连接表，对每一个 u，用 cycleId[u]将其代替。

第二步可以这样做：

1  function visit(u):
2      for each vertex v among the children of u:
3          visit(v)
4
5      if there is a back-edge going up from u:
6          cycleId[u] = the index of that back-edge
7      else:
8          cycleId[u] = u
9          for each vertex v among the children of u:
10             if cycleId[v] != v and there is no back-edge going down from v:
11                 cycleId[u] = cycleId[v]

移除边来构建二分图

问题 3

：考虑一个无向图，找到所有的边，将这些边移除后，图将变为二分图。

这题是

codeforces 19E – Fairy

。官方没有发布题解，但一个

非官方题解

提到了用复杂的数据结构动态树解答。利用 DFS 树，我们可以不使用高级的数据结构来解答这题。

在最初的问题中，图需要被连接。然而，明显可得：

\cdot

$\cdot$

如果图没有非二分部件，那么移除任意一条边都可以

\cdot

$\cdot$

如果图的多个非二分部件，那么不可能将其边为二分图

那么，唯一需要有意思的情况就是当、只有一个非二分部件的情况。显然移除的边显然来自该部件，所以我们可以假设只有一个部件。从现在开始，我们假设我们有一个非二分的连通图。

让我们建立该图的 DFS 树，我们可以将点涂成黑和白来让每个树边都连接一个黑色顶点和一个白色顶点。一些回边肯会连接同样颜色的顶点，我们称其为

矛盾边

。

结论 7

：回边 uv 满足条件当且仅当 uv 是唯一的矛盾边。

证明：如果我们移除唯一的矛盾边，图的所有边就都连接不同的颜色，那么就成为二分图；如果有其他的矛盾边或我们移除了一条非矛盾边，遗留的矛盾边将继续构成奇数环并且图无法成为二分图。

结论 8

：回边 uv 满足条件当且仅当所有矛盾边都是它的回边。

证明：如果我们移除了一条树边，生成树将会分成两个部分：uv 的子树和剩余的部分。此时剩余的所有树边依旧连接着不同颜色的点。因此，唯一使二分图成立的方法使将将 uv 的子树中的所有节点翻转颜色。

移除树边 uv 满足条件当且仅当翻转颜色后消除了所有的矛盾而且不产生新的矛盾。这只在矛盾边都是连接 uv 的子树和图的剩余部分是成立。

因此，我们可以这样解决问题：

1.建立图的 DFS 树并将它涂成两色；

2.如果只存在一条矛盾的回边，将其加入答案；

3.用动态规划去计算每一条树边有多少矛盾边和多少非矛盾边跨越它；

4.如果一条树边包含了所有的矛盾回边且没有非矛盾回边跨越它，将其加入答案

有向型

如果要建立有向图的 DFS 树怎么办？我们重新进行深度优先遍历：

1 function visit(u):
2     mark u as visited
3     for each vertex v among the neighbours of u:
4         if v is not visited:
5             mark the edge u->v
6             call visit(v)