博客

Mumford-Shah(1989年提出)

其主要思想是：通过分段平滑函数找到原始图像的最佳逼近。

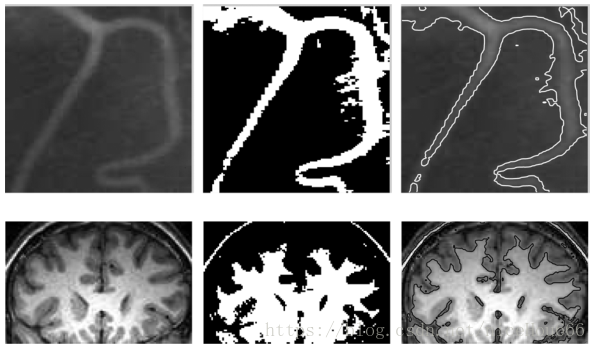
下图来自维基百科，左1是原图，左2是梯度图像，左3是MS模型的边缘图像，最右是最终结果。从结果可以看出，这样的近似图像忽略了很多小细节。

由于使用了图像梯度信息，在轮廓内作灰度平均，使得Mumford-Shah模型不适用于灰度不均匀的医学图像，难以反映细节，对噪声也相对敏感。另外，由于未知轮廓和函数非凸性，能量函数难以最小化。

Chan-vese,即CV模型（2001年提出）

主要思想是：用分段常数函数代替Mumford-Shah中的分段平滑函数。

由于分段常数函数是轮廓内外灰度平均值，即考虑的是灰度均匀的情况。所以当灰度不均匀时，分割结果会有较大差异。如下图。另外，CV模型为了在曲线演化过程中，保持符号距离函数特性，所以需要不断初始化水平集函数，计算量大，效率低。相较于MS模型，利用了水平集方法最小化能量函数。