博客

前言

LBP（Local Binary Pattern，局部二值模式）是一种用来描述图像局部纹理特征的算子；它具有旋转不变性和灰度不变性等显著的优点。它是首先由T. Ojala, M.Pietikäinen, 和 D. Harwood 在1994年提出，用于纹理特征提取。而且，提取的特征是图像的局部的纹理特征。常用的特征描述子有：HOG、Harris、LBP等等，其中LBP是最为简单且有效的一种特征描述子，下面来介绍一下LBP以及其变种，附带python的程序实现。

1、LBP

概述

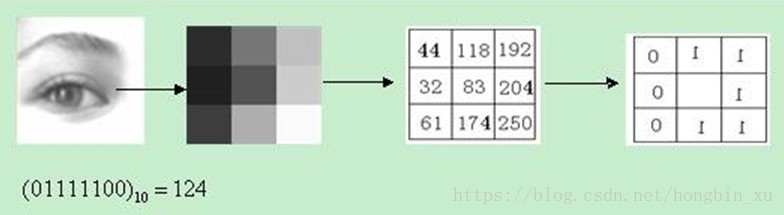
原始的LBP算子定义在一个








3


×


3










3

×

3


$3\times 3$
的窗口内，以窗口中心像素为阈值，与相邻的8个像素的灰度值比较，若周围的像素值大于中心像素值，则该位置被标记为1;，否则标记为0。如此可以得到一个8位二进制数（通常还要转换为10进制，即LBP码，共256种），将这个值作为窗口中心像素点的LBP值，以此来反应这个








3


×


3










3

×

3


$3\times 3$
区域的纹理信息。

示意图如下：（摘自网络）

公式

表示成数学公式：

$$LBP(x_c, y_c) = \sum_{p=1}^{8}s(I(p) - I(c)) * 2^p$$

其中，








p










p


$p$
表示









3


×


3

$3\times 3$
窗口中除中心像素点外的第








p










p


$p$
个像素点；









I




(


c


)

$I(c)$
表示中心像素点的灰度值，








I




(


p


)










I

(

p

)


$I(p)$
表示领域内第








p










p


$p$
个像素点的灰度值；









s


(


x


)

$s(x)$
公式如下：

$$s(x) = \begin{cases} 1, x \geq 0 \\ 0, otherwise \end{cases}$$

直观解释

通过上述变换，我们可以将一个像素点与8个相邻点之间的差值关系用一个数表示，这个数的范围是0-255。因为LBP记录的是中心像素点与领域像素点之间的差值，所以当光照变化引起像素灰度值同增同减时，LBP变化并不明显。所以可以认为LBP对与光照变化不敏感，LBP检测的仅仅是图像的纹理信息，因此，进一步还可以将LBP做直方图统计，这个直方图可以用来作为纹理分析的特征算子。

程序实现

完整程序会在最后一起给出，这里就只给出函数了。

def LBP(src):
    '''
    :param src:灰度图像
    :return:
    '''
    height = src.shape[0]
    width = src.shape[1]
    dst = src.copy()

    lbp_value = np.zeros((1,8), dtype=np.uint8)
    neighbours = np.zeros((1,8), dtype=np.uint8)
    for x in range(1, width-1):
        for y in range(1, height-1):
            neighbours[0, 0] = src[y - 1, x - 1]
            neighbours[0, 1] = src[y - 1, x]
            neighbours[0, 2] = src[y - 1, x + 1]
            neighbours[0, 3] = src[y, x - 1]
            neighbours[0, 4] = src[y, x + 1]
            neighbours[0, 5] = src[y + 1, x - 1]
            neighbours[0, 6] = src[y + 1, x]
            neighbours[0, 7] = src[y + 1, x + 1]

            center = src[y, x]

            for i in range(8):
                if neighbours[0, i] > center:
                    lbp_value[0, i] = 1
                else:
                    lbp_value[0, i] = 0

            lbp = lbp_value[0, 0] * 1 + lbp_value[0, 1] * 2 + lbp_value[0, 2] * 4 + lbp_value[0, 3] * 8 \
                + lbp_value[0, 4] * 16 + lbp_value[0, 5] * 32 + lbp_value[0, 6] * 64 + lbp_value[0, 0] * 128

            dst[y, x] = lbp

    return dst

运行结果

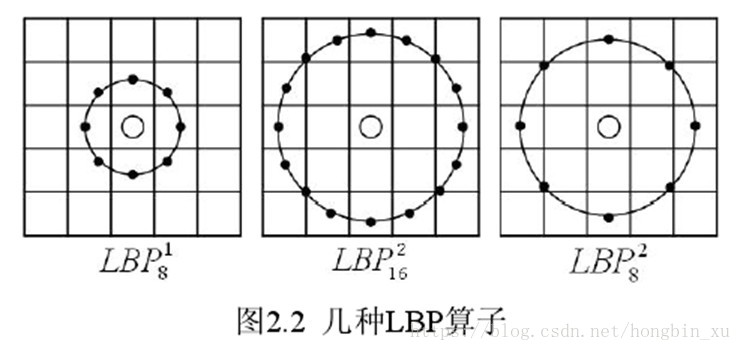
2、圆形LBP

概念

我们不难注意到原始的LBP算子仅仅只是覆盖了很小的一个








3


×


3










3

×

3


$3 \times 3$
领域的范围，这显然不能满足提取不同尺寸纹理特征的需求。为了适应不同尺度的纹理特征，并达到灰度和旋转不变性的要求，Ojala等对LBP 算子进行了改进，将 3×3邻域扩展到任意邻域，并用圆形邻域代替了正方形邻域。改进后的LBP 算子允许在半径为 R 的圆形邻域内有任意多个像素点。

假设半径为R的圆形区域内含有P个采样点的LBP算子：



对比上图，发现当








p


=


8


,


R


=


1










p

=

8

,

R

=

1


$p=8,R=1$
时，圆形LBP基本与原始LBP一致；比如在








p


=


16


,


R


=


2










p

=

16

,

R

=

2


$p=16,R=2$
时，圆形边界上的点可能不是整数或正好落在某个像素格子内，可能位于交界处，所以这种情况下，可以使用双线性插值法来计算该点的像素值。

公式

圆形LBP跟原始公式很像，无非就是增加了两个变量：采样点数








P












P


$P$
以及采样圆形领域半径









R

$R$
。

表示成数学公式：

L


B





P










P




,


R









(





x






c







,





y








c







)


=





∑








P












p


=


1









s


(


I




(


p


)


−


I




(


c


)


)


∗





2






p















L

B

P

P

,

R

(

x

c

,

y

c

)

=

∑

p

=

1

P

s

(

I

(

p

)

−

I

(

c

)

)

∗

2

p


$LBP_{P,R}(x_c, y_c) = \sum_{p=1}^{P}s(I(p) - I(c)) * 2^p$

其中，








p










p


$p$
表示圆形区域中总计









P

$P$
个采样点中的第








p










p


$p$
个采样点（注意大小写区分开了）；









I




(


c


)

$I(c)$
表示中心像素的灰度值，








I




(


p


)










I

(

p

)


$I(p)$
表示圆形边界像素点中第








p










p


$p$
个点的灰度值。

总共有









p

$p$
个点在圆形边界上，那么那些点的坐标如何计算？通过下面公式计算：

$$\begin{cases} x_p = x_c + R * \cos(\frac{2 \pi p}{P}) \\ y_p = y_c - R * \sin(\frac{2 \pi p}{P})\end{cases}$$

s


(


x


)










s

(

x

)


$s(x)$
公式与原始LBP中的一样，公式如下：

$$s(x) = \begin{cases} 1, x \geq 0 \\ 0, otherwise \end{cases}$$

程序实现

def circular_LBP(src, radius, n_points):
    height = src.shape[0]
    width = src.shape[1]
    dst = src.copy()
    src.astype(dtype=np.float32)
    dst.astype(dtype=np.float32)

    neighbours = np.zeros((1, n_points), dtype=np.uint8)
    lbp_value = np.zeros((1, n_points), dtype=np.uint8)
    for x in range(radius, width - radius - 1):
        for y in range(radius, height - radius - 1):
            lbp = 0.
            # 先计算共n_points个点对应的像素值，使用双线性插值法
            for n in range(n_points):
                theta = float(2 * np.pi * n) / n_points
                x_n = x + radius * np.cos(theta)
                y_n = y - radius * np.sin(theta)

                # 向下取整
                x1 = int(math.floor(x_n))
                y1 = int(math.floor(y_n))
                # 向上取整
                x2 = int(math.ceil(x_n))
                y2 = int(math.ceil(y_n))

                # 将坐标映射到0-1之间
                tx = np.abs(x - x1)
                ty = np.abs(y - y1)

                # 根据0-1之间的x，y的权重计算公式计算权重
                w1 = (1 - tx) * (1 - ty)
                w2 = tx * (1 - ty)
                w3 = (1 - tx) * ty
                w4 = tx * ty

                # 根据双线性插值公式计算第k个采样点的灰度值
                neighbour = src[y1, x1] * w1 + src[y2, x1] * w2 + src[y1, x2] * w3 + src[y2, x2] * w4

                neighbours[0, n] = neighbour

            center = src[y, x]

            for n in range(n_points):
                if neighbours[0, n] > center:
                    lbp_value[0, n] = 1
                else:
                    lbp_value[0, n] = 0

            for n in range(n_points):
                lbp += lbp_value[0, n] * 2**n

            # 转换到0-255的灰度空间，比如n_points=16位时结果会超出这个范围，对该结果归一化
            dst[y, x] = int(lbp / (2**n_points-1) * 255)

    return dst

运行结果

当








R


=


1


,


P




=


8










R

=

1

,

P

=

8


$R=1, P=8$
时：

当








R


=


2


,


P




=


16










R

=

2

,

P

=

16


$R=2,P=16$
时：

当








R


=


4


,


P




=


16










R

=

4

,

P

=

16


$R=4,P=16$
时：

3、旋转不变LBP

概念

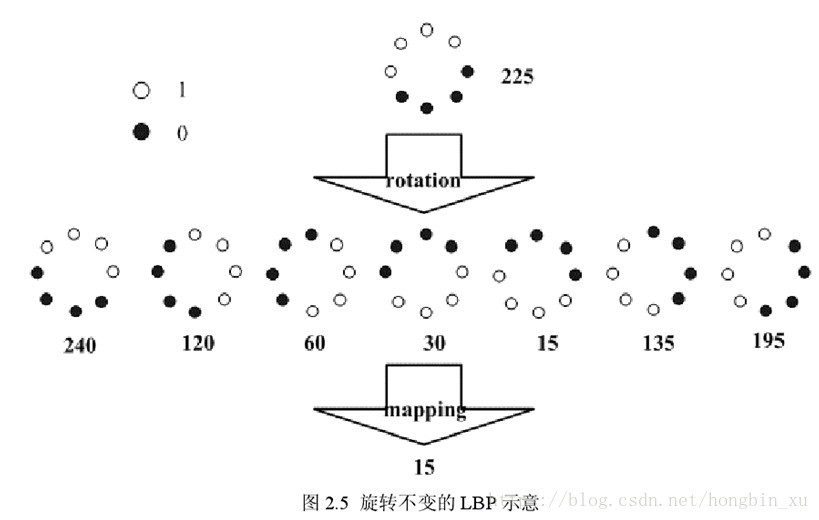
从原始LBP的定义来看，LBP算子是灰度不变的，但不是旋转不变的。图像旋转的话就会得到不同的LBP值。

Maenpaa等人又将 LBP算子进行了扩展，提出了具有旋转不变性的 LBP 算子，即不断旋转圆形邻域得到一系列初始定义的 LBP值，取其最小值作为该邻域的 LBP 值。



如上图所示（图片摘自网络），原始LBP得到的数值转化为二进制编码，对它进行循环移位操作，有8种情况（包括自身）。取其中最小的一个值，比如图中就对应着15，这个值是旋转不变的，因为对图像做旋转操作等价与上面8种移位的过程了，而8种情况都对应同一个值，即8个值中的最小值15，即拥有了旋转不变特性。

数学公式

LBP值计算方式与原始的LBP一样，这里不做赘述。

区别在于对LBP的结果进行二进制编码，并做循环位移，取所有结果中最小的那个值：

$$LBP_{P,R}^{rot} = \min{\{ROR(LBP_{P,R}, i) | i = 0,...,P-1\}}$$

程序实现

先定义计算旋转后灰度值的函数，以保证旋转不变的结果：

def value_rotation(num):
    value_list = np.zeros((8), np.uint8)
    temp = int(num)
    value_list[0] = temp
    for i in range(7):
        temp = ((temp << 1) | (temp / 128)) % 256
        value_list[i+1] = temp
    return np.min(value_list)

定义旋转不变LBP主体函数：

def rotation_invariant_LBP(src):
    height = src.shape[0]
    width = src.shape[1]
    dst = src.copy()

    lbp_value = np.zeros((1, 8), dtype=np.uint8)
    neighbours = np.zeros((1, 8), dtype=np.uint8)
    for x in range(1, width - 1):
        for y in range(1, height - 1):
            neighbours[0, 0] = src[y - 1, x - 1]
            neighbours[0, 1] = src[y - 1, x]
            neighbours[0, 2] = src[y - 1, x + 1]
            neighbours[0, 3] = src[y, x - 1]
            neighbours[0, 4] = src[y, x + 1]
            neighbours[0, 5] = src[y + 1, x - 1]
            neighbours[0, 6] = src[y + 1, x]
            neighbours[0, 7] = src[y + 1, x + 1]

            center = src[y, x]

            for i in range(8):
                if neighbours[0, i] > center:
                    lbp_value[0, i] = 1
                else:
                    lbp_value[0, i] = 0

            lbp = lbp_value[0, 0] * 1 + lbp_value[0, 1] * 2 + lbp_value[0, 2] * 4 + lbp_value[0, 3] * 8 \
                  + lbp_value[0, 4] * 16 + lbp_value[0, 5] * 32 + lbp_value[0, 6] * 64 + lbp_value[0, 0] * 128

            # 旋转不变值
            dst[y, x] = value_rotation(lbp)

    return dst

运行结果

4、均匀模式LBP（uniform LBP）

概念

基本LBP算子可以产生8位二进制数对应的











2






8







−


1










2

8

−

1


$2^8-1$
种模式，对于半径为








R










R


$R$
的圆形区域内含有









P

$P$
个采样点，会有











2






P









−


1










2

P

−

1


$2^P-1$
种模式。很显然，随着采样点数








P












P


$P$
的增加，二进制模式的种类是呈指数趋势增长的。过多的二进制模式对于纹理的表达是不利的，过于复杂且庞大的信息量，很明显违背了提取特征信息的初衷，我们需要的只是尽可能少且具有代表性的特征，因此需要对LBP得到的二进制模式种类进行降维，使用更少的数据量来最好地表示图像的信息。而这种降维的方法就是uniform LBP。

均匀模式LBP（uniform LBP），就是限制一个二进制序列从0到1或从1到0的跳变次数不超过2次。

为解决二进制模式过多的问题，提高统计性，Ojala提出了采用一种“等价模式”(Uniform Pattern)来对LBP算子的模式种类进行降维。Ojala等认为，在实际图像中，绝大多数LBP模式最多只包含两次从1到0或从0到1的跳变。因此，Ojala将“等价模式”定义为：当某个LBP所对应的循环二进制数从0到1或从1到0最多有两次跳变时，该LBP所对应的二进制就称为一个等价模式类。如00000000(0次跳变)，00000111(只含一次从0到1的跳变)，10001111(先由1跳到0，再由0跳到1，共两次跳变)都是等价模式类。除等价模式类以外的模式都归为另一类，称为混合模式类，例如10010111(共四次跳变)。通过这样的改进，二进制模式的种类大大减少，而不会丢失任何信息。模式数量由原来的2P种减少为 P ( P-1)+2种，其中P表示邻域集内的采样点数。对于3×3邻域内8个采样点来说，二进制模式由原始的256种减少为58种，即：它把值分为59类，58个uniform pattern为一类，其它的所有值为第59类。这样直方图从原来的256维变成59维。这使得特征向量的维数更少，并且可以减少高频噪声带来的影响。

数学公式

$$U(LBP_{P,R}) = |s[I(P-1) - I(c)] - s[I(0) - I(c)]| + |\sum_{p=1}^{P-1}{s[I(p) - I(c)] - s[I(p-1) - I(c)]}|$$

上式目的就是统计二进制数的跳变次数。

跳变次数小于等于2，则各自代表一类，跳变次数大于2的所有情况归为一类。

程序实现

为简便起见，我是在原始LBP的基础之上做uniform LBP的。所以总共会有8位二进制数，跳变数量小于2的模式共有58种，加上剩余的所有模式归为一种，加起来共59种。我将跳变数量小于2的模式分别定义为1-58，剩余的情况，即第59中情况，定义为0。

计算跳变次数的函数：

def getHopCnt(num):
    '''
    :param num:8位的整形数，0-255
    :return:
    '''
    if num > 255:
        num = 255
    elif num < 0:
        num = 0

    num_b = bin(num)
    num_b = str(num_b)[2:]

    # 补0
    if len(num_b) < 8:
        temp = []
        for i in range(8-len(num_b)):
            temp.append('0')
        temp.extend(num_b)
        num_b = temp

    cnt = 0
    for i in range(8):
        if i == 0:
            former = num_b[-1]
        else:
            former = num_b[i-1]
        if former == num_b[i]:
            pass
        else:
            cnt += 1

    return cnt

归一化函数，将像素值归一化，并重新投影到新的灰度空间，默认最大值为255，最小值为0：

def img_max_min_normalization(src, min=0, max=255):
    height = src.shape[0]
    width = src.shape[1]
    if len(src.shape) > 2:
        channel = src.shape[2]
    else:
        channel = 1

    src_min = np.min(src)
    src_max = np.max(src)

    if channel == 1:
        dst = np.zeros([height, width], dtype=np.float32)
        for h in range(height):
            for w in range(width):
                dst[h, w] = float(src[h, w] - src_min) / float(src_max - src_min) * (max - min) + min
    else:
        dst = np.zeros([height, width, channel], dtype=np.float32)
        for c in range(channel):
            for h in range(height):
                for w in range(width):
                    dst[h, w, c] = float(src[h, w, c] - src_min) / float(src_max - src_min) * (max - min) + min

    return dst

uniform LBP的主体函数：其中norm表示是否要进行归一化，因为使用uniform LBP出来的值是0-58的，显示效果可能不明显。

def uniform_LBP(src, norm=True):
    '''
    :param src:原始图像
    :param norm:是否做归一化到【0-255】的灰度空间
    :return:
    '''
    table = np.zeros((256), dtype=np.uint8)
    temp = 1
    for i in range(256):
        if getHopCnt(i) <= 2:
            table[i] = temp
            temp += 1

    height = src.shape[0]
    width = src.shape[1]
    dst = np.zeros([height, width], dtype=np.uint8)
    dst = src.copy()

    lbp_value = np.zeros((1, 8), dtype=np.uint8)
    neighbours = np.zeros((1, 8), dtype=np.uint8)
    for x in range(1, width - 1):
        for y in range(1, height - 1):
            neighbours[0, 0] = src[y - 1, x - 1]
            neighbours[0, 1] = src[y - 1, x]
            neighbours[0, 2] = src[y - 1, x + 1]
            neighbours[0, 3] = src[y, x - 1]
            neighbours[0, 4] = src[y, x + 1]
            neighbours[0, 5] = src[y + 1, x - 1]
            neighbours[0, 6] = src[y + 1, x]
            neighbours[0, 7] = src[y + 1, x + 1]

            center = src[y, x]

            for i in range(8):
                if neighbours[0, i] > center:
                    lbp_value[0, i] = 1
                else:
                    lbp_value[0, i] = 0

            lbp = lbp_value[0, 0] * 1 + lbp_value[0, 1] * 2 + lbp_value[0, 2] * 4 + lbp_value[0, 3] * 8 \
                  + lbp_value[0, 4] * 16 + lbp_value[0, 5] * 32 + lbp_value[0, 6] * 64 + lbp_value[0, 0] * 128

            dst[y, x] = table[lbp]

    if norm is True:
        return img_max_min_normalization(dst)
    else:
        return dst

运行结果

5、均匀模式+旋转不变模式LBP

概念

使用uniform LBP加上旋转不变模式LBP来提取特征，概念上面都介绍了，无非就是叠加起来而已。

数学公式

先计算跳变次数：

$$U(LBP_{P,R}) = |s[I(P-1) - I(c)] - s[I(0) - I(c)]| + |\sum_{p=1}^{P-1}{s[I(p) - I(c)] - s[I(p-1) - I(c)]}|$$

跳变次数小于等于2，则各自代表一类，跳变次数大于2的所有情况归为一类。得到的结果设为








L


B





P










u


n


i










P




,


R

















L

B

P

P

,

R

u

n

i


$LBP_{P,R}^{uni}$
。

再对其二进制编码做循环移位，求出最小值。

$$LBP_{P,R}^{rot, uni} = \min{\{ROR(LBP_{P,R}^{uni}, i) | i = 0,...,P-1\}}$$

程序实现

def rotation_invariant_uniform_LBP(src):
    table = np.zeros((256), dtype=np.uint8)
    temp = 1
    for i in range(256):
        if getHopCnt(i) <= 2:
            table[i] = temp
            temp += 1

    height = src.shape[0]
    width = src.shape[1]
    dst = np.zeros([height, width], dtype=np.uint8)
    dst = src.copy()

    lbp_value = np.zeros((1, 8), dtype=np.uint8)
    neighbours = np.zeros((1, 8), dtype=np.uint8)
    for x in range(1, width - 1):
        for y in range(1, height - 1):
            neighbours[0, 0] = src[y - 1, x - 1]
            neighbours[0, 1] = src[y - 1, x]
            neighbours[0, 2] = src[y - 1, x + 1]
            neighbours[0, 3] = src[y, x - 1]
            neighbours[0, 4] = src[y, x + 1]
            neighbours[0, 5] = src[y + 1, x - 1]
            neighbours[0, 6] = src[y + 1, x]
            neighbours[0, 7] = src[y + 1, x + 1]

            center = src[y, x]

            for i in range(8):
                if neighbours[0, i] > center:
                    lbp_value[0, i] = 1
                else:
                    lbp_value[0, i] = 0

            lbp = lbp_value[0, 0] * 1 + lbp_value[0, 1] * 2 + lbp_value[0, 2] * 4 + lbp_value[0, 3] * 8 \
                  + lbp_value[0, 4] * 16 + lbp_value[0, 5] * 32 + lbp_value[0, 6] * 64 + lbp_value[0, 0] * 128

            dst[y, x] = table[lbp]

    dst = img_max_min_normalization(dst)
    for x in range(width):
        for y in range(height):
            dst[y, x] = value_rotation(dst[y, x])

    return dst

运行结果

后记

这篇博客中总结了几种经典的LBP算子：原始LBP算子、圆形LBP算子、旋转不变模式LBP算子、均匀模式LBP算子（uniform LBP）、均匀模式+旋转不变模式LBP算子。LBP算子的原理不难，程序实现也很容易，但是功能确也很强大，用处还是很广的。下次有时间再整理一下其他变种形式的LBP。

参考资料：

1. 
   https://blog.csdn.net/u014114990/article/details/50913592
   
2. 
   https://blog.csdn.net/matrix_space/article/details/50481641
   
3. 
   https://blog.csdn.net/zouxy09/article/details/7929531
   
4. 
   http://blog.163.com/yuyang_tech/blog/static/21605008320138642618253/
   
5. 
   https://www.2cto.com/kf/201712/705037.html
   

附录：完整代码

# *_*coding:utf-8 *_*
# author: 许鸿斌
# 经典LBP算法复现：原始LBP、Uniform LBP、旋转不变LBP、旋转不变的Uniform LBP

import numpy as np
import cv2
import matplotlib.pyplot as plt
import math

def LBP(src):
    '''
    :param src:灰度图像
    :return:
    '''
    height = src.shape[0]
    width = src.shape[1]
    # dst = np.zeros([height, width], dtype=np.uint8)
    dst = src.copy()

    lbp_value = np.zeros((1,8), dtype=np.uint8)
    neighbours = np.zeros((1,8), dtype=np.uint8)
    for x in range(1, width-1):
        for y in range(1, height-1):
            neighbours[0, 0] = src[y - 1, x - 1]
            neighbours[0, 1] = src[y - 1, x]
            neighbours[0, 2] = src[y - 1, x + 1]
            neighbours[0, 3] = src[y, x - 1]
            neighbours[0, 4] = src[y, x + 1]
            neighbours[0, 5] = src[y + 1, x - 1]
            neighbours[0, 6] = src[y + 1, x]
            neighbours[0, 7] = src[y + 1, x + 1]

            center = src[y, x]

            for i in range(8):
                if neighbours[0, i] > center:
                    lbp_value[0, i] = 1
                else:
                    lbp_value[0, i] = 0

            lbp = lbp_value[0, 0] * 1 + lbp_value[0, 1] * 2 + lbp_value[0, 2] * 4 + lbp_value[0, 3] * 8 \
                + lbp_value[0, 4] * 16 + lbp_value[0, 5] * 32 + lbp_value[0, 6] * 64 + lbp_value[0, 0] * 128

            dst[y, x] = lbp

    return dst

def getHopCnt(num):
    '''
    :param num:8位的整形数，0-255
    :return:
    '''
    if num > 255:
        num = 255
    elif num < 0:
        num = 0

    num_b = bin(num)
    num_b = str(num_b)[2:]

    # 补0
    if len(num_b) < 8:
        temp = []
        for i in range(8-len(num_b)):
            temp.append('0')
        temp.extend(num_b)
        num_b = temp

    cnt = 0
    for i in range(8):
        if i == 0:
            former = num_b[-1]
        else:
            former = num_b[i-1]
        if former == num_b[i]:
            pass
        else:
            cnt += 1

    return cnt

def uniform_LBP(src, norm=True):
    '''
    :param src:原始图像
    :param norm:是否做归一化到【0-255】的灰度空间
    :return:
    '''
    table = np.zeros((256), dtype=np.uint8)
    temp = 1
    for i in range(256):
        if getHopCnt(i) <= 2:
            table[i] = temp
            temp += 1

    height = src.shape[0]
    width = src.shape[1]
    dst = np.zeros([height, width], dtype=np.uint8)
    dst = src.copy()

    lbp_value = np.zeros((1, 8), dtype=np.uint8)
    neighbours = np.zeros((1, 8), dtype=np.uint8)
    for x in range(1, width - 1):
        for y in range(1, height - 1):
            neighbours[0, 0] = src[y - 1, x - 1]
            neighbours[0, 1] = src[y - 1, x]
            neighbours[0, 2] = src[y - 1, x + 1]
            neighbours[0, 3] = src[y, x - 1]
            neighbours[0, 4] = src[y, x + 1]
            neighbours[0, 5] = src[y + 1, x - 1]
            neighbours[0, 6] = src[y + 1, x]
            neighbours[0, 7] = src[y + 1, x + 1]

            center = src[y, x]

            for i in range(8):
                if neighbours[0, i] > center:
                    lbp_value[0, i] = 1
                else:
                    lbp_value[0, i] = 0

            lbp = lbp_value[0, 0] * 1 + lbp_value[0, 1] * 2 + lbp_value[0, 2] * 4 + lbp_value[0, 3] * 8 \
                  + lbp_value[0, 4] * 16 + lbp_value[0, 5] * 32 + lbp_value[0, 6] * 64 + lbp_value[0, 0] * 128

            dst[y, x] = table[lbp]

    if norm is True:
        return img_max_min_normalization(dst)
    else:
        return dst

def img_max_min_normalization(src, min=0, max=255):
    height = src.shape[0]
    width = src.shape[1]
    if len(src.shape) > 2:
        channel = src.shape[2]
    else:
        channel = 1

    src_min = np.min(src)
    src_max = np.max(src)

    if channel == 1:
        dst = np.zeros([height, width], dtype=np.float32)
        for h in range(height):
            for w in range(width):
                dst[h, w] = float(src[h, w] - src_min) / float(src_max - src_min) * (max - min) + min
    else:
        dst = np.zeros([height, width, channel], dtype=np.float32)
        for c in range(channel):
            for h in range(height):
                for w in range(width):
                    dst[h, w, c] = float(src[h, w, c] - src_min) / float(src_max - src_min) * (max - min) + min

    return dst

def value_rotation(num):
    value_list = np.zeros((8), np.uint8)
    temp = int(num)
    value_list[0] = temp
    for i in range(7):
        temp = ((temp << 1) | (temp / 128)) % 256
        value_list[i+1] = temp
    return np.min(value_list)

def rotation_invariant_LBP(src):
    height = src.shape[0]
    width = src.shape[1]
    # dst = np.zeros([height, width], dtype=np.uint8)
    dst = src.copy()

    lbp_value = np.zeros((1, 8), dtype=np.uint8)
    neighbours = np.zeros((1, 8), dtype=np.uint8)
    for x in range(1, width - 1):
        for y in range(1, height - 1):
            neighbours[0, 0] = src[y - 1, x - 1]
            neighbours[0, 1] = src[y - 1, x]
            neighbours[0, 2] = src[y - 1, x + 1]
            neighbours[0, 3] = src[y, x - 1]
            neighbours[0, 4] = src[y, x + 1]
            neighbours[0, 5] = src[y + 1, x - 1]
            neighbours[0, 6] = src[y + 1, x]
            neighbours[0, 7] = src[y + 1, x + 1]

            center = src[y, x]

            for i in range(8):
                if neighbours[0, i] > center:
                    lbp_value[0, i] = 1
                else:
                    lbp_value[0, i] = 0

            lbp = lbp_value[0, 0] * 1 + lbp_value[0, 1] * 2 + lbp_value[0, 2] * 4 + lbp_value[0, 3] * 8 \
                  + lbp_value[0, 4] * 16 + lbp_value[0, 5] * 32 + lbp_value[0, 6] * 64 + lbp_value[0, 0] * 128

            dst[y, x] = value_rotation(lbp)

    return dst

def rotation_invariant_uniform_LBP(src):
    table = np.zeros((256), dtype=np.uint8)
    temp = 1
    for i in range(256):
        if getHopCnt(i) <= 2:
            table[i] = temp
            temp += 1

    height = src.shape[0]
    width = src.shape[1]
    dst = np.zeros([height, width], dtype=np.uint8)
    dst = src.copy()

    lbp_value = np.zeros((1, 8), dtype=np.uint8)
    neighbours = np.zeros((1, 8), dtype=np.uint8)
    for x in range(1, width - 1):
        for y in range(1, height - 1):
            neighbours[0, 0] = src[y - 1, x - 1]
            neighbours[0, 1] = src[y - 1, x]
            neighbours[0, 2] = src[y - 1, x + 1]
            neighbours[0, 3] = src[y, x - 1]
            neighbours[0, 4] = src[y, x + 1]
            neighbours[0, 5] = src[y + 1, x - 1]
            neighbours[0, 6] = src[y + 1, x]
            neighbours[0, 7] = src[y + 1, x + 1]

            center = src[y, x]

            for i in range(8):
                if neighbours[0, i] > center:
                    lbp_value[0, i] = 1
                else:
                    lbp_value[0, i] = 0

            lbp = lbp_value[0, 0] * 1 + lbp_value[0, 1] * 2 + lbp_value[0, 2] * 4 + lbp_value[0, 3] * 8 \
                  + lbp_value[0, 4] * 16 + lbp_value[0, 5] * 32 + lbp_value[0, 6] * 64 + lbp_value[0, 0] * 128

            dst[y, x] = table[lbp]

    dst = img_max_min_normalization(dst)
    for x in range(width):
        for y in range(height):
            dst[y, x] = value_rotation(dst[y, x])

    return dst

def circular_LBP(src, radius, n_points):
    height = src.shape[0]
    width = src.shape[1]
    # dst = np.zeros([height, width], dtype=np.uint8)
    dst = src.copy()
    src.astype(dtype=np.float32)
    dst.astype(dtype=np.float32)

    neighbours = np.zeros((1, n_points), dtype=np.uint8)
    lbp_value = np.zeros((1, n_points), dtype=np.uint8)
    for x in range(radius, width - radius - 1):
        for y in range(radius, height - radius - 1):
            lbp = 0.
            for n in range(n_points):
                theta = float(2 * np.pi * n) / n_points
                x_n = x + radius * np.cos(theta)
                y_n = y - radius * np.sin(theta)

                # 向下取整
                x1 = int(math.floor(x_n))
                y1 = int(math.floor(y_n))
                # 向上取整
                x2 = int(math.ceil(x_n))
                y2 = int(math.ceil(y_n))

                # 将坐标映射到0-1之间
                tx = np.abs(x - x1)
                ty = np.abs(y - y1)

                # 根据0-1之间的x，y的权重计算公式计算权重
                w1 = (1 - tx) * (1 - ty)
                w2 = tx * (1 - ty)
                w3 = (1 - tx) * ty
                w4 = tx * ty

                # 根据双线性插值公式计算第k个采样点的灰度值
                neighbour = src[y1, x1] * w1 + src[y2, x1] * w2 + src[y1, x2] * w3 + src[y2, x2] * w4

                neighbours[0, n] = neighbour

            center = src[y, x]

            # print('center:{}; neighbours:{}'.format(center, neighbours))

            for n in range(n_points):
                if neighbours[0, n] > center:
                    lbp_value[0, n] = 1
                else:
                    lbp_value[0, n] = 0

            # print('lbp_value:{}'.format(lbp_value))

            for n in range(n_points):
                lbp += lbp_value[0, n] * 2**n
                # print('lbp_value[0, n] * 2**n : {}'.format(lbp_value[0, n] * 2**n))

            # print('lbp_value transformed:{}'.format(lbp))

            dst[y, x] = int(lbp / (2**n_points-1) * 255)

            # print('dst value of [{}, {}]:{}'.format(y, x, dst[y,x]))

    return dst

def disp_test_result(img, gray, dst, mode=0):
    '''
    :param mode:0,opencv显示图片；1,matplotlib显示图片。
    :return:
    '''
    if mode == 0:
        cv2.imshow('src', img)
        cv2.imshow('gray', gray)
        cv2.imshow('LBP', dst)
        cv2.waitKey()
        cv2.destroyAllWindows()
    else:
        plt.figure()
        plt.subplot(131)
        plt.imshow(img)
        plt.title('src')

        plt.subplot(132)
        plt.imshow(gray, cmap='gray')
        plt.title('gray')

        plt.subplot(133)
        plt.imshow(dst, cmap='gray')
        plt.title('LBP')

        plt.show()


if __name__ == '__main__':
    img = cv2.imread('test.jpg')
    gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
    # dst = LBP(gray)
    dst1 = uniform_LBP(gray)
    # dst2 = rotation_invariant_LBP(gray)
    dst3 = rotation_invariant_uniform_LBP(gray)
    # dst4 = circular_LBP(gray, radius=4, n_points=16)

    # disp_test_result(img, gray, dst, mode=0)
    disp_test_result(img, gray, dst1, mode=0)
    # disp_test_result(img, gray, dst2, mode=0)
    # disp_test_result(img, gray, dst3, mode=0)
    # disp_test_result(img, gray, dst4, mode=0)