博客

稳定性定义：相同的值在排序结束之后的相对次序不变。

1. 冒泡排序

每一轮相邻两个值之间比较，大小顺序相反的交换位置，最后的值总是最大。

稳定性：稳定

def BubbleSort(alist):
    """冒泡排序 """
    #最坏时间复杂度= O(n^2)
     #用count控制如某一层从头到尾的比较中没有做任何交换，说明顺序已经正确，不用继续比,可使最优复杂度变为 O(n)
    n = len(alist)
    for i in range(n-1) # 外层控制一共走多少次       
        count = 0 
        for j in range(n-1-i):
            # 内层控制从头走到尾
            if alist[j] > alist[j+1]:#因为没有等号，所以相邻值相等时不改变次序，是稳定的算法
                alist[j],alist[j+1] = alist[j+1],alist[j]
            	count += 1
        if count == 0:
            return


if __name__ == "__main__":
    li = [32,54,12,45,23,13,67,12,43]
    print(li)
    BubbleSort(li)
    print(li)

2. 选择排序

思路：认为左边有序右边无序。将右边无序的数值中找到最小的，第二小的依次与左边的交换位置。

稳定性：考虑从小到大排列，第一个元素是10，被最小值调换之后就排到列表中的10后面.所以不稳定

def SelectSort(alist):
    """选择排序""" # 最优和最坏时间复杂度都是O(n^2) 不稳定
    n = len(alist)
    for i in range(n-1):
        min_index = i
        for j in range(i+1,n):
            if alist[j] < alist[min_index]:
                min_index = j
        alist[i],alist[min_index] = alist[min_index],alist[i]

if __name__ == "__main__":
    li = [32,54,12,45,23,13,67,12,43]
    print(li)
    SelectSort(li)
    print(li)

3. 插入排序

假设左边有序，右边无序。

先拿出第一个元素，每一轮将右边剩下的元素与左边比较，依次往前挪直到前面一个比他小

• 最优时间复杂度：O(n) （升序排列，序列已经处于升序状态）
• 最坏时间复杂度：O(n^2) （升序排列，序列处于降序状态）
• 稳定性：稳定

# def InsertSort(alist):
#     n = len(alist)
#     for i in range(1,n):
#         j = i  # j代表内层循环起始值
#         while j > 0:
#             if alist[j] < alist[j-1]:
#                alist[j],alist[j-1] = alist[j-1],alist[j]
#                j -= 1
#             else:
#                 break
""" 等价2个for循环："""
def InsertSort(alist):
    n = len(alist)
    for i in range(n-1):
        for j in range(i+1,0,-1):
            if alist[j] < alist[j-1]: #因为没有等号，所以相邻值相等时不改变次序，是稳定的算法
                alist[j], alist[j-1] = alist[j-1], alist[j]

if __name__ == "__main__":
    li = [32,11,54,129,45,23,13,67,12,43]
    print(li)
    InsertSort(li)
    print(li)

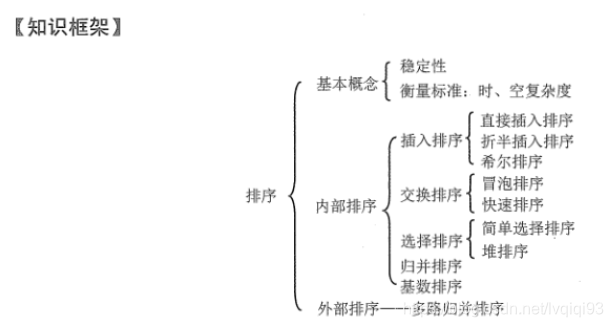
4. 希尔排序

是不需要递归的简单算法中执行效率较高的排序算法。属于插入排序的优化算法。

稳定性：不稳定

def ShellSort(alist):
    """希尔排序"""
    n = len(alist)
    gap = n // 2
    while gap >= 1:
        for i in range(gap, n):
            j = i
            while j > 0:
                if alist[j] < alist[j-gap]:
                    alist[j], alist[j-gap] = alist[j-gap], alist[j]
                    j = j -gap
                else:
                    break
        gap = gap // 2

if __name__ == "__main__":
    li = [32,11,54,129,45,23,13,67,12,43]
    print(li)
    ShellSort(li)
    print(li)

5. 快速排序

• 最优时间复杂度：O(nlogn)

• 最坏时间复杂度：O(n^2)

• 稳定性：不稳定

• 通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列.

• 把第一个元素拿出来，设为中间元素mid，两头各一个游标，各自和中间元素mid比较，右边边必须比mid大，否则和左边游标处空出来的位置交换，并且换左边移动，满足条件则不动，继续往中间移动。指定左右两个游标都移动到中间，这时两边分别递归继续快速排序。

def QuickSort(alist,start,end):
    """快速排序"""
    #start和end是不会变的开头和末尾元素，left和right会移动
    if start >= end:
        return
    mid = alist[start]
    left = start
    right = end

    while left < right:
        while left < right and alist[right] >= mid:
            right -= 1
        alist[left] = alist[right]

        while left < right and alist[left] < mid:
            left += 1
        alist[right] = alist[left]

    alist[left] = mid
    QuickSort(alist,start,left-1)
    QuickSort(alist, left+1, end)

if __name__ == "__main__":
    li = [32,11,3,129,45,9,13,67,12,43]
    print(li)
    QuickSort(li,0,len(li)-1)
    print(li)

快排时间复杂度计算：

一共递归了logN次，每次O(N), 一共(NlogN)

最坏情况：有序数组，每次只搞定一个数O(N^2)

问题：与数据状况有关，如果分偏了，对复杂度有影响。

6. 归并排序

先将数组分成两组，各自用递归的方法排好序，然后用left和right两个游标各自指向第一个元素，哪个小就添加到最后排序数组，并且把游标向右移动一个。

def MergeSort(alist):
    n = len(alist)
    mid = n // 2
    if 1 == n:
        return alist

    #对左伴部分进行归并排序
    left_li = MergeSort(alist[:mid]) #T(N/2)
    #对右伴部分进行归并排序
    right_li = MergeSort(alist[mid:])#T(N/2)
    #左神解法：T(N)=2T(N/2)+O(N) 所以根据master公式 复杂度是NlogN
    #只考虑单个分的情况是对半，不考虑一共对半了多少次
    
    #合并两个有序集合
    left, right = 0, 0
    result = []
    while left < len(left_li) and right < len(right_li):
        # 此处等号意味着左右相等的2个值，左边还是先添加进来，保证稳定性
        if left_li[left] <= right_li[right]: 
            result.append(left_li[left])
            left += 1
        else:
            result.append(right_li[right])
            right += 1

    
    #下俩其实只执行了一个
    result += left_li[left:]
    result += right_li[right:]

    return result

if __name__ == "__main__":
    li = [32,11,3,129,45,9,13,67,12,43]
    print(li)
    sorted_li=MergeSort(li)
    print(sorted_li)

7. 根排序

不稳定

def HeapSort(alist):
    """堆排序"""
    if alist ==[] or len(alist) < 2:
        return alist

    for i in range(len(alist)):
        heapInsert(alist, i) #建立大根堆结构
    heapSize = len(alist)
    alist[0], alist[heapSize - 1] = alist[heapSize - 1], alist[0] #大根堆首尾交换
    heapSize -= 1 #去掉最末尾的节点（也就是此时大根堆的最大值）
    while heapSize > 0:
        heapify(alist, 0, heapSize)
        alist[0], alist[heapSize - 1] = alist[heapSize - 1], alist[0]
        heapSize -= 1
    return alist


def heapInsert(alist, index):
    """建立大根堆结构： 当前节点比他的父节点大的时候，交换，跳到index的父节点的位置，再往上跟他的父节点比较，直到整个完全形成大根堆的结构"""
    """ 大根堆：每一个子树的根节点都是这个树里的最大值 """
    # 考虑父节点不能小于0
    while alist[index] > alist[(index - 1) // 2] and ((index - 1) // 2 >= 0): 
        alist[index], alist[(index - 1) // 2] = alist[(index - 1) // 2], alist[index]
        index = (index - 1) // 2 #跳到index的父节点的位置


#判断根节点的数字是不是最大，不是就一直往下沉，直到重新恢复到大根堆的结构
def heapify(alist, index, heapSize):
    left = index * 2 + 1
    while left < heapSize:
        # 取到左右两个叶节点的最大值
        largest = left + 1 if left + 1 < heapSize and alist[left + 1] > alist[left] else left  
        # 将左右两个叶节点的最大值跟其父节点比较取最大值
        largest = largest if alist[largest] > alist[index] else index 
        # 等价于上一行代码中 alist[largest] <= alist[index] 父节点比两个子节点大或相等
        if largest == index:  
            break             # 不需再往下沉了
        # largest ！= index 父亲往下沉
        alist[largest], alist[index] = alist[index], alist[largest] 
        index = largest #父亲index变成了他较大孩子的下标
        left = index * 2 + 1

if __name__ == "__main__":
    li = [32,11,54,129,45,23,13,67,12,43]
    print(li)
    HeapSort(li)
    print(li)

8.桶排序

def maxGap(alist):
    """不是桶排序 给定一个数组，求如果排序之后，相邻两数的最大差值，
    要求时间复杂度O(N)，且要求不能用非基于比较的排序。"""
    if alist is None or len(alist) < 2:
        return 0

    n = len(alist)
    minNum = min(alist)
    maxNum = max(alist)

    if minNum == maxNum:
        return 0

    bucketBool = [False] * (n + 1)
    bucketMax = [0] * (n + 1)
    bucketMin = [0] * (n + 1)

    for i in range(n):
        bid = bucket(alist[i], n, minNum, maxNum)  # 得出来自几号桶
        bucketMin[bid] = min(bucketMin[bid], alist[i]) if bucketBool[bid] else alist[i]
        bucketMax[bid] = max(bucketMax[bid], alist[i]) if bucketBool[bid] else alist[i]
        bucketBool[bid] = True
    res = 0
    lastMax = bucketMax[0]
    # 找到每一个非空桶和离他最近的左边的非空桶，用当前最小减前一个桶的最大
    for i in range(n + 1):
        if bucketBool[i]:
            res = max(res, bucketMin[i] - lastMax)
            lastMax = bucketMax[i]
    return res

#确定这个数来自几号桶 n:桶的个数
def bucket(num, n, minNum, maxNum):
    return int((num - minNum) * n / (maxNum - minNum))

时间复杂度和稳定性比较：

稳定的：冒泡排序，插入排序，归并排序

不稳定的：选择排序，希尔排序，堆排序，快速排序

排序算法的选择：

基本数据类型（int,double,char,float）相同值无差异，不用在意稳定性：

快速排序

自定义字段，在意稳定性：

归并排序

不管什么类型，数组长度很短（长度<60）代码极其简单，忽略常数项，样本量很低的情况下：

插排

O（n^2)

参考：

王道考研算法与数据结构