一、为什么MySQL采用B+树
哈希索引
理想时间复杂度为 O(1)
适用场景:适用于等值查询的场景,内存数据的索引
典型实现:Redis,
MySQL
的
memory
引擎
平衡二叉树索引
查询和更新的时间复杂度都是 O(log(n))
适用场景:内存数据的索引,但不适合磁盘数据的索引,可以认为
树的高度决定了磁盘 I/O 的次数
,百万数据树高约为
20(lg(1000000)/ lg(2))
BTree 索引
BTree
其实就是
n
叉树,分叉多意味着节点中的孩子(
key
)多,树高自然就降低了
分叉数由页大小和行(包括 key 与
value
)大小决定
假设页大小为 16k,每行 40
个字节,那么分叉数就为
16k / 40
≈
410
而分叉为 410,则百万数据树高约为3,仅
3
次 I/O 就能找到所需数据
局部性原理
:
每次
I/O
按页为单位读取数据,把多个
key
相邻
的行放在同一页中(每页就是树上一个节点),能进一步减少 I/O
B+ 树索引
在
BTree
的基础上做了改进,索引上只存储
key
,这样能进一步增加分叉数,假设
key
占
13
个字节,那么一页数据分叉数可以到
1260
,树高可以进一步下降为
2
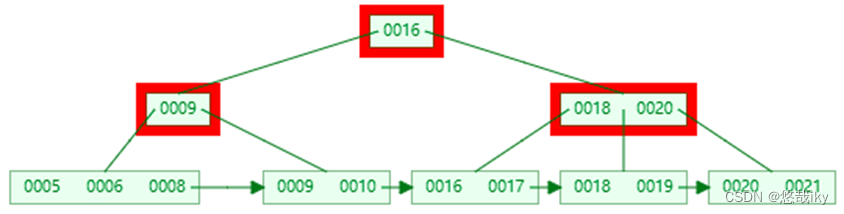
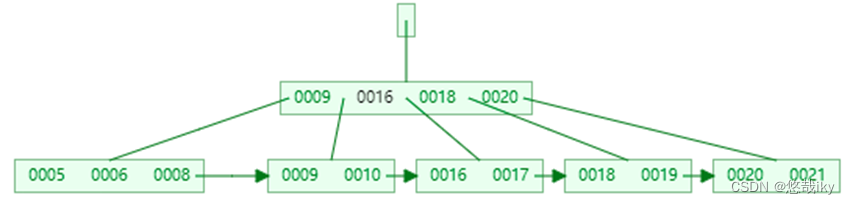
二、BTree vs B+Tree
1、BTree key
及
value
在每个节点上,无论叶子还是非叶子节点,而
B+Tree
普通节点只存
key
,叶子节点才存储
key
和
value
2、B+Tree
叶子节点用链表连接,可以方便范围查询及全表遍历

3、无论 BTree
还是
B+Tree
,每个叶子节点到根节点距离都相同,
B+Tree
必须到达叶子节点才能找到
value

注:这两张图都是仅画了 key,未画 value
二、
B+Tree
新增
key
(以
5
阶为例)
插入
19
、
20
、
21
、
22
、
6
、
9

插入
7
,当前结点的
key
个数到达
5
,需要分裂

分裂后 key 7 进入到父结点中,这时父节点
key
个数也到达
5

非叶子节点分裂规则
:左子结点包含前
(m-1)/2
个
key
,将中间的
key
进位到父结点中(
不保留
),右子节点包含剩余的
key
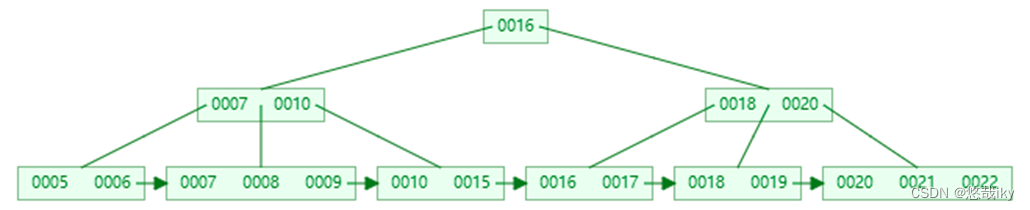
三、
B+Tree
查询
key
以查询 15
为例
第一次 I/O
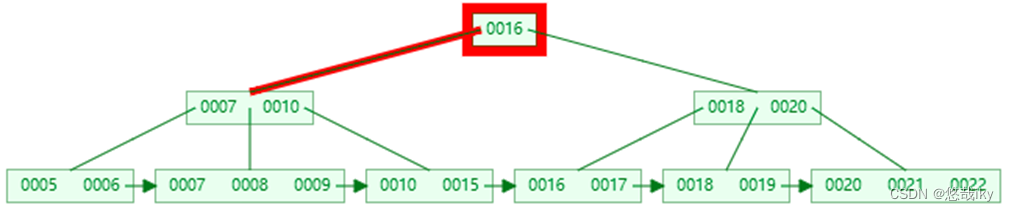
第二次
I/O
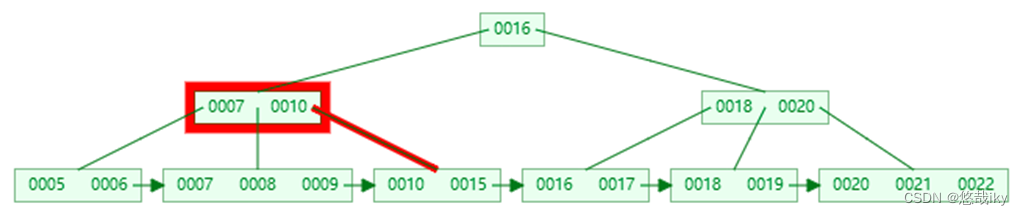
第三次 I/O
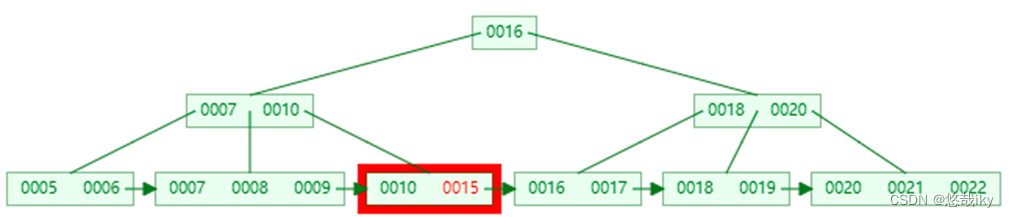
四、
B+Tree
删除
key
叶子节点
的
key
删除,初始状态
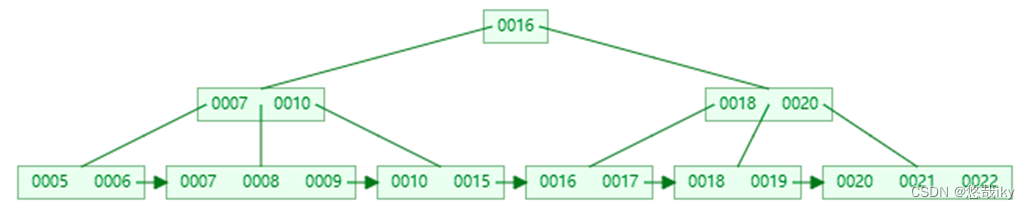
删完有富余
。即删除后结点的
key
的个数
>
m/2 – 1
,删除操作结束,例如删除
22
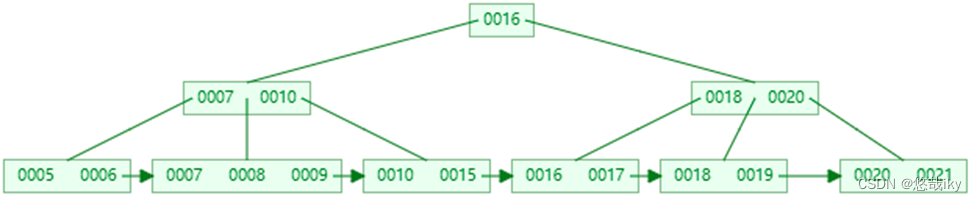
删完没富余,但兄弟节点有富余
。即兄弟结点
key
有富余(
>
m/2 – 1
),向兄弟结点借一个记录,同时替换父节点,例如删除
15

兄弟节点也不富余,合并兄弟叶子节点
。即
兄弟节点合并成一个新的叶子结点,并删除父结点中的
key
,将当前结点指向父结点,例如删除
7
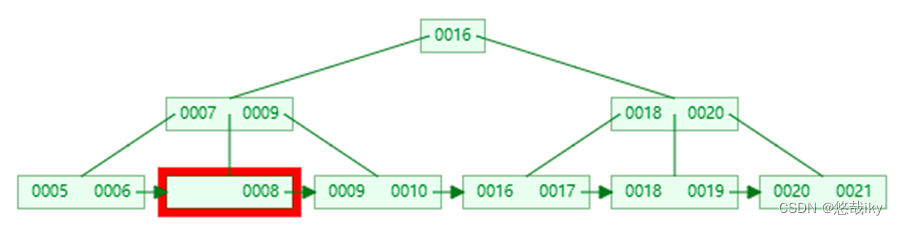
也需要删除非叶子节点中的
7
,并替换父节点保证区间仍有效
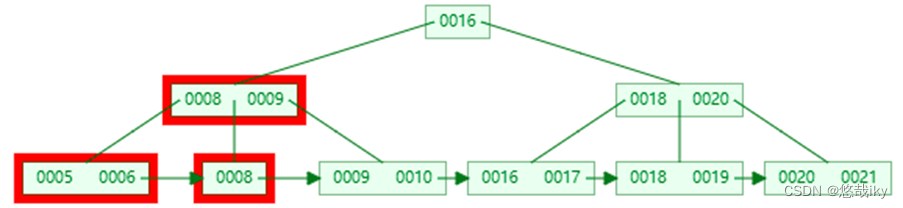
左右兄弟都不够借,合并
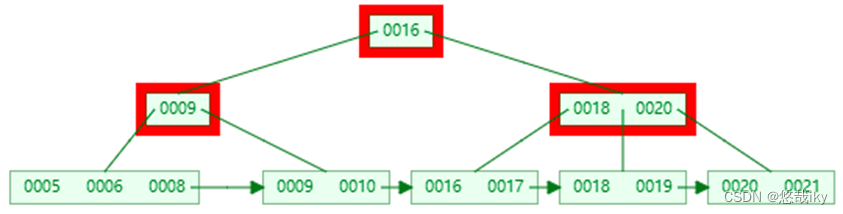
回顾删除要点:
1.
非叶子节点
key
的个数
>
m/2 – 1
,则删除操作结束,否则执行
2
2. 若兄弟结点有富余,父结点
key
下移,兄弟结点
key
上移,删除结束,否则执行
3
3. 兄第节点没富余,当前结点和兄弟结点及父结点合并成一个新的结点。重复
1