逻辑回归的极大似然推导:
由于似然函数是样本的函数,需要知道其分布,并且假设相互独立。



上述公式就推导出梯度下降更新的方向
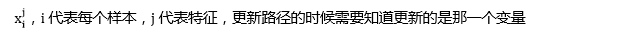
梯度更新的方法:

逻辑回归编程实现(
按步骤手工编程
)
假设我们有一个数据,共有100个样本,含两个x变量,x1、x2,一个目标变量y。数据如下:
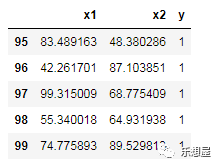
我们的目标是求出参数θ0、θ1、θ2。
步骤1:定义sigmoid函数
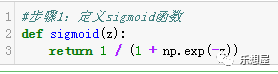
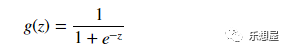
logistic转化成预测概率。
步骤2:定义线性回归函数z的表达式

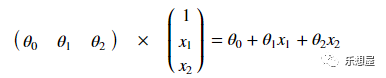
步骤3:定义初始值
θ

步骤4:根据对数似然函数,写出J(
θ
),并写出损失函数
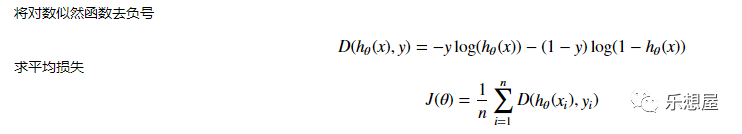

当
θ初始值为0时,此时的损失函数的值为ln(0.5)
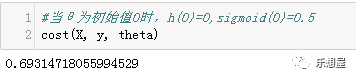
步骤5:计算每个参数的梯度下降方向
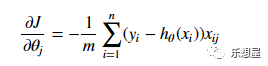

步骤6:定义样本数据的刷新重排
每次迭代后需要重新刷新数据:

步骤7:梯度下降算法模块
1)设置不同的迭代停止策略,
共有三种策略:根据迭代次数、根据两次迭代目标值的变化、根据梯度值。

2)定义梯度下降公式。

3)定义梯度下降的方法

梯度下降有三种方法:
-
批量梯度下降法:
在更新参数时使用所有样本来进行更新.
-
随机梯度下降法:
批量梯度下降法原理类似,区别在与求梯度时没有用所有的n个样本的数据,而是仅仅选取1个样本来求梯度。和批量梯度下降法是两个极端值
-
小批量梯度下降法:
是批量梯度下降法和随机梯度下降法的折中,也就是对于n个样本,我们采用m个样子来迭代,1<m<n。一般可以取m=10,当然根据样本的数据,可以调整这个m的值。
步骤8:梯度下降算法实施案例。
可尝试不同的方法和策略
1、对比不同的停止策略,采用批量梯度下降法
1)策略1:采用限制迭代次数停止法。迭代策略设置为5000次。最后损失值为0.63
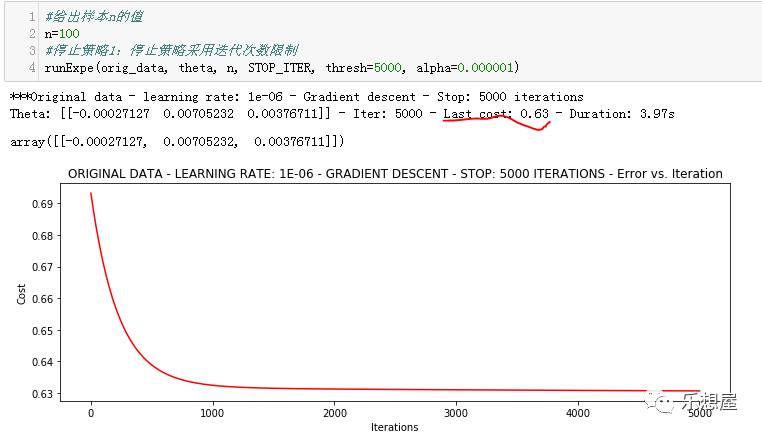
2)策略2:采用目标值变化的限制,两次目标值的变动小于0.000001时则停止。大约迭代了109901次,最后的损失值为0.38.
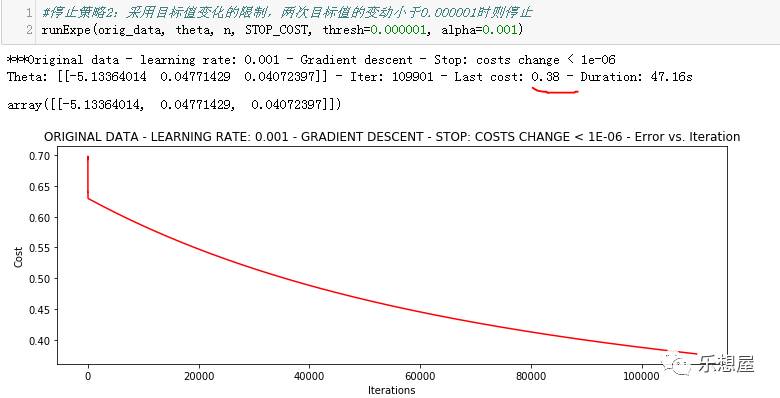
3)停止策略3:采用梯度值的方法限制,梯度值的限制为0.05。大约迭代了140045次,最后的损失值为0.49.
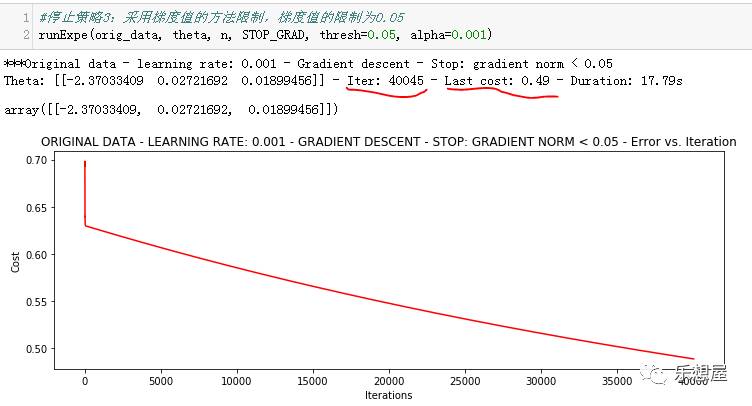
也可以看出迭代次数越多效果越好。
2、对比不同梯度下降法
1)采用随机梯度下降法:取
1个样本来求梯度
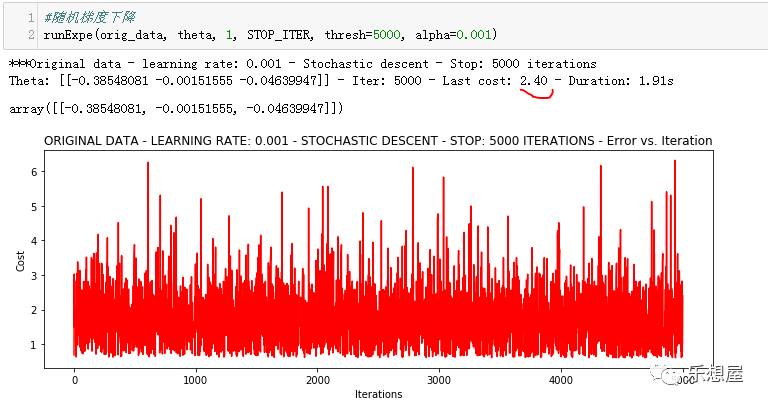
可以看出模型不稳定。尝试调小学习率,增加迭代次数
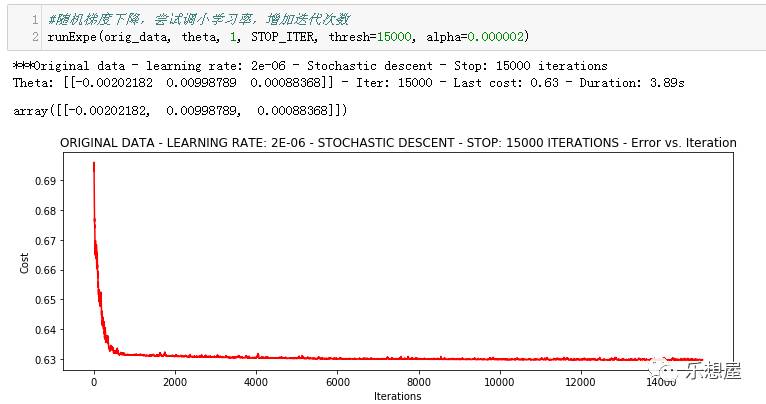
2)采用小批量梯度下降法:取10个样本来求梯度
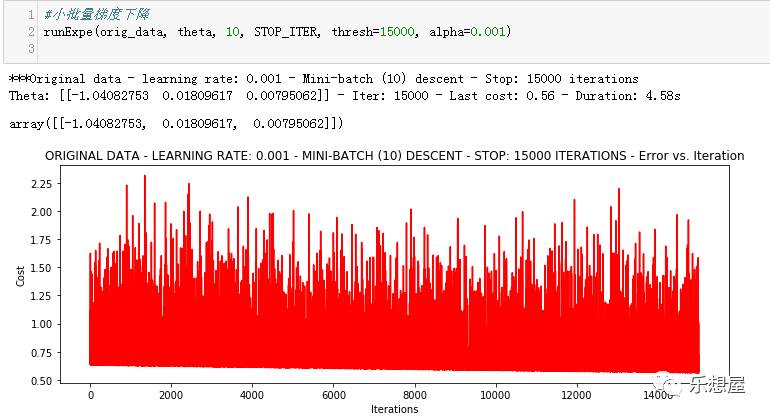
结果仍然不太稳定。
3、数据标准化之后的处理
尝试下对数据进行标准化 将数据按其属性(按列进行)减去其均值,然后除以其方差。最后得到的结果是,对每个属性/每列来说所有数据都聚集在0附近,方差值为1。

1)批量梯度下降法,迭代5000次,求解目标值为0.38.数据预处理非常重要,可以提高迭代效率。
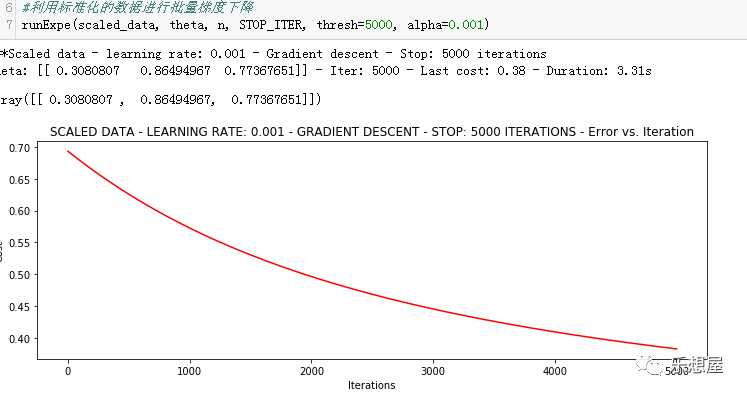
2)批量梯度下降法,迭代次数增加,可以使损失函数降的更多
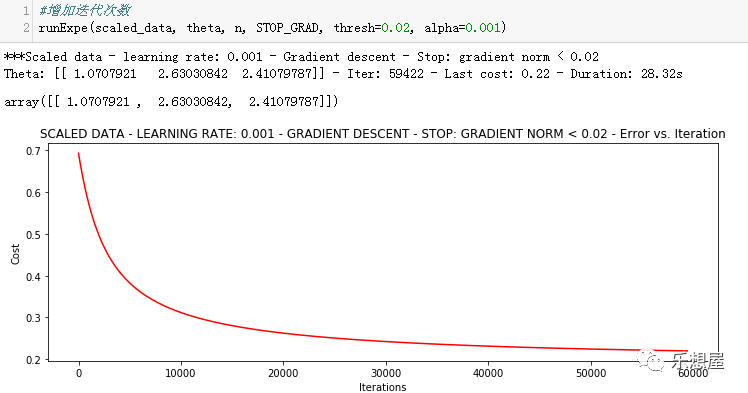
更多的迭代次数会使得损失下降的更多。
3)小批量梯度下降法,增加迭代次数,下降效果更好
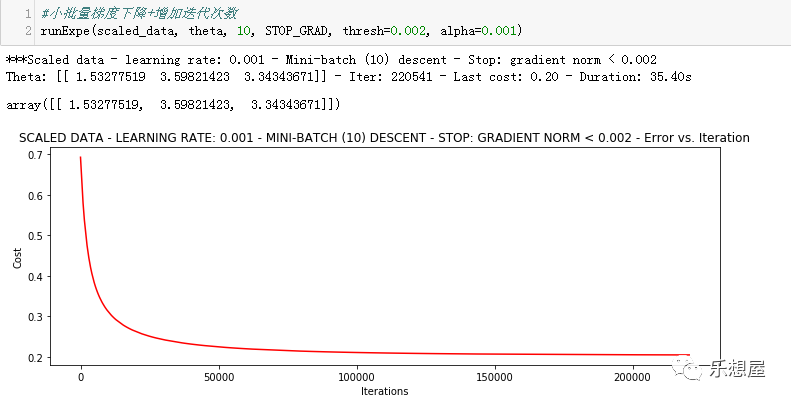
步骤10:定义精确度,并求解优化前及优化后的精度对比。

计算精度
当theta=
array([[ 0., 0., 0.]])时,计算精度为:

当theta为梯度优化后的值时,求出的精度为89%
Theta: [[ 1.49844241 3.5261332 3.27347064]]

关于逻辑回归的知识,可参考:
统计知识3:逻辑回归函数、Sigmoid函数、极大似然
关于梯度下降的知识,可参考:
统计知识4:梯度下降