博客

1. 线性回归算法

• 解决回归问题
• 算法简单
• 许多强大的非线性模型的基础
• 结果具有可解释性
• 蕴含机器学习中很多重要的思想

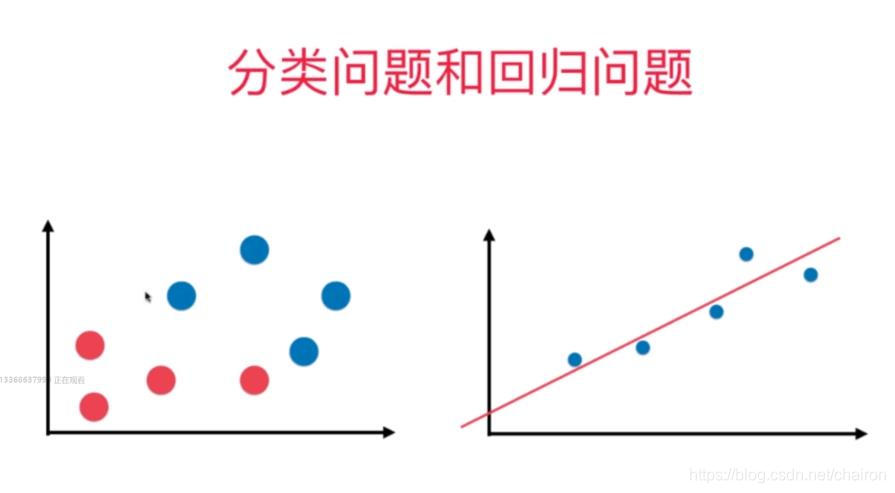
2. 分类问题和回归问题

分类问题的坐标轴都表示属性，坐标轴中的点的颜色表示分类结果；回归问题的y轴表示预测结果，x轴表示属性（简单线性回归）

3. 简单线性回归

• 适用于只有一个属性
• 找到最佳拟合曲线y=a*x+b
• 找到参数a，b使每一个样本点x_train的y_train和y_predict之间的差距尽量小（找到参数a，b，使损失函数/效用函数尽可能小/大

4. 参数学习算法的基本思路

1. 通过分析问题，确定问题的损失函数或效用函数
2. 通过最优化损失函数或者效用函数，获得机器学习的模型
3. 参数学习只要获得参数，无需存储训练数据集

5. 简单线性回归的实现

 1. 求a,b----->最小二乘法（对a、b求偏导，使偏导数为0）
 2. 获得y=a*x+b的曲线

实现 simple linear regrassion

import numpy as np
import matplotlib.pyplot as plt

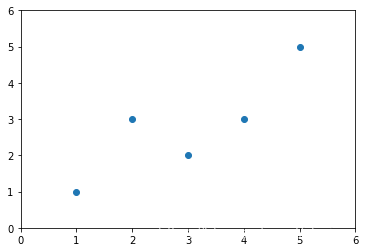
x=np.array([1.,2.,3.,4.,5.])
y=np.array([1.,3.,2.,3.,5.])

plt.scatter(x,y)
plt.axis([0,6,0,6])

[0, 6, 0, 6]

1. 根据公式计算a,b的值

x_mean=np.mean(x)
y_mean=np.mean(y)

1. 使用for循环

num=0.0
d=0.0
for x_i,y_i in zip(x,y):
    num+=(x_i-x_mean)*(y_i-y_mean)
    d+=(x_i-x_mean)**2

**2. 可以用向量的乘法计算num，d，向量相乘，等于对应元素相乘相加**

num=(x-x_mean).dot(y-y_mean)
d=(x-x_mean).dot(x-x_mean)

a=num/d
b=y_mean-a*x_mean

a

0.8

b

0.39999999999999947

2. 绘制预测的曲线

y_hat=a*x+b

plt.scatter(x,y)
plt.plot(x,y_hat,color='r')
plt.axis([0,6,0,6])

[0, 6, 0, 6]

3. 新数据进行预测

x_predict=6
y_predict=a*x_predict+b

y_predict

5.2