MATLAB滤波常用函数
模拟滤波器阶数选择函数
buttord
功能:计算butterworth模拟滤波器的阶数
调用格式:
[n,Wn]=buttord(Wp,Ws,Rp,Rs,'s');
% 参数中的n是求出模拟滤波器最小的阶数,Wn是等效低通滤波器的截止频率;Wp和Ws分别是通带和阻带的频率(截止频率)。当Wp>Ws时,为高通滤波器,当Wp和Ws为二元矢量时,为带通或带阻滤波器,这时求出的Wn也是二元矢量。
%此处buttord可替换为 cheb1ord,cheb2ord,ellipord函数,相应为切比雪夫I型,切比雪夫II型,椭圆滤波器。
butter
功能:butterworth模拟滤波器的设计
调用格式:
[b,a]=butter(n,Wn,'s');
[b,a]=butter(n,Wn,'ftype','s')
%此处buttord可替换为 cheb1ord,cheb2ord,ellipord函数,相应为切比雪夫I型,切比雪夫II型,椭圆滤波器。
%当Wn=[W1 W2](W1<W2)时,表示设计一个带通滤波器,函数将产生一个2n阶的数字带通滤波器,其通带频率为W1<w<W2。
% 当带有参数'ftype'时,表示可设计出高通或带阻滤波器。
% 当ftype=high时,设计出截止频率为Wn的高通滤波器。
%当ftype=stop时,设计出带阻滤波器,这时Wn=[W1 W2],且阻带频率为W1<w<W2。
一、带通滤波
例1
对信号data实现20-350Hz的带通滤波,信号data的采样频率为Fs,代码如下:
fp1=[50,300];fs1=[20, 350];
Fs2=Fs/2;
Wp=fp1/Fs2; Ws=fs1/Fs2;
Rp=1; Rs=30;
[n,Wn]=cheb2ord(Wp,Ws,Rp,Rs);
[b1,a1]=cheby2(n,Rs,Wn);
y=filter(b1,a1,data);%经过filter滤波之后得到的数据y则是经过带通滤波后的信号数据
这里需要解释一个问题,为何需要将通带和阻带除以采样频率的一半Fs2呢?
我们都知道一句话,叫做
时域采样,频域延拓
。频域的延拓主要是以周期为
2
π
2\pi
2
π
进行延拓。也即意味着,经过离散时间傅里叶变换DTFT后,在频域是以
2
π
2\pi
2
π
为周期的。具体参考这篇文章
时域采样与频域延拓
。因此,我们的滤波器实际是这样的
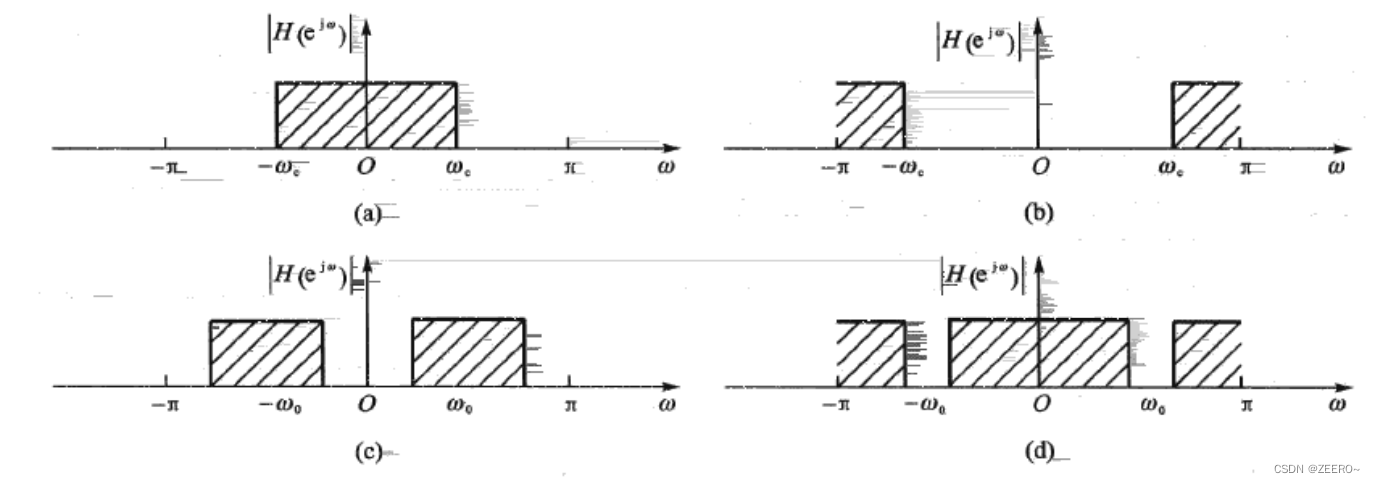
a,b,c,d分别表示低通滤波、高通滤波、带通滤波、带阻滤波。因此,我们所定义的通带和阻带频率需要进行归一化到
π
\pi
π
。我们知道,采样周期
F
s
Fs
F
s
对应的频率周期为
2
π
2\pi
2
π
,因此要归一化到
π
\pi
π
,则需要除以采样频率的一半。
额外说明
评论区有人问其中的
R
p
R_{p}
R
p
和
R
s
R_{s}
R
s
是什么,这里解释一下,分别代表通带起伏和阻带衰减。理想状态下,我们可以得到例如说50Hz的高通滤波器,如上图(b)所示。但在实际过程中,
w
c
−
∞
w_{c}-\infin
w
c
−
∞
这段频率带范围内幅频响应不可能是一条平坦的直线,会像波浪线一样起伏变化。因此
R
p
R_{p}
R
p
代表的是通带起伏,用来反映起伏程度如何。
R
p
R_{p}
R
p
越大,起伏程度越高。
R
s
R_{s}
R
s
则是代表阻带衰减的幅度大小。这里用个类似的图来说明一下。
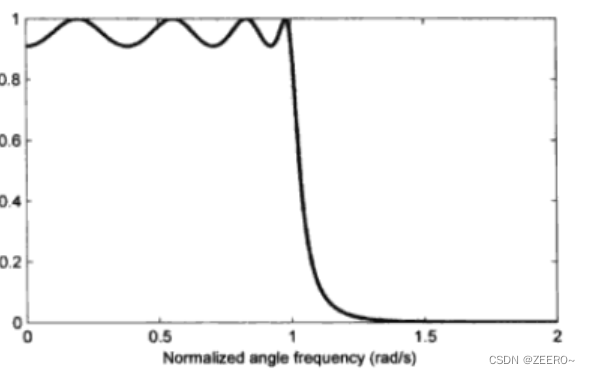
图片中的波纹线反映了通带起伏。
二、带阻滤波
例2
对信号data实现50Hz带阻滤波
fp1=[10,250];fs1=[49, 51];
Fs2=Fs/2;
Wp=fp1/Fs2; Ws=fs1/Fs2;
Rp=1; Rs=30;
[n,Wn]=cheb2ord(Wp,Ws,Rp,Rs);
[b2,a2]=cheby2(n,Rs,'stop');
y=filter(b2,a2,data);%经过filter滤波之后得到的数据y则是经过带通滤波后的信号数据
低通
例3
对信号data实现20Hz的低通滤波
fp1=10;fs=30;
Fs2=Fs/2;
Wp=fp1/Fs2; Ws=fs1/Fs2;
Rp=1; Rs=30;
[n,Wn]=buttord(Wp,Ws,Rp,Rs);
[b2,a2]=butter(n,Wn,'s'');
y=filter(b2,a2,data);%经过filter滤波之后得到的数据y则是经过带通滤波后的信号数据
高通
例4
对信号data实现100Hz的高通滤波
fp1=90;fs1=110;
Fs2=Fs/2;
Wp=fp1/Fs2; Ws=fs1/Fs2;
Rp=1; Rs=30;
[n,Wn]=buttord(Wp,Ws,Rp,Rs);
[b2,a2]=butter(n,Wn,'high','s');
y=filter(b2,a2,data);%经过filter滤波之后得到的数据y则是经过带通滤波后的信号数据
一些经验
实际过程中,实际设计过程中更常用的形式是
[b,a]=butter(n,Wn,ftype); %ftype可以为low,high,bandpass,stop
这个时候,通带起伏和阻带衰减被设定为默认值,n为滤波器阶数,根据自己经验进行设定。如果为
bandpass
和
stop
的话,滤波器的阶数则为
2n
。一般来说,阶数越高,在过渡带内衰减的就越快。上述
[n,Wn]=buttord(Wp,Ws,Rp,Rs);
中返回的是最低截止频率。可以先用buttord函数简答试下,然后取一个较为满意的阶数即可。例如,假如采样频率为1000Hz,要设计一个4阶、50Hz的高通滤波器,可以这样实现
Fs=1000;
Fs2=Fs/2;
[b,a]=butter(4,50/Fs2,'high');
参考资料
1、《学以致用 深入浅出数字信号处理》 江志宏