2010年,Jorge Mu˜noz-Gama and Josep Carmona提出了一种新的精度度量方法,该方法基于当模型偏离日志时计算这些情况的简单思想。此外,还提出了一种基于日志的模型遍历方法,避免了检查其整体行为。
1.背景介绍
上一节所提出的精确度度量(称为高级行为适当性)仅限于比较模型中事件与日志中事件之间的排序关系。这种方法需要对模型的状态空间进行彻底的探索,这对于表现出高度并发性的大型模型来说是不切实际的,即出现
状态空间爆炸
问题。
因此,提出了一种测量精确度的新技术,其目的是:i)补充其他技术提供的精确度信息,ii)克服依赖于检查工业或现实生活模型和日志的一致性的固有复杂性,以及iii)为后续过程扩展提供有用信息,即可以扩展模型以更好地反映日志的阶段。
该方法可以总结如下:
给定模型和日志,计算模型的行为,该行为仅限于日志
(下图中的灰色背景部分)。
日志和模型行为之间的边界定义了模型偏离日志的关键点,
称这些为
逃逸边缘(escaping edges)
。通过量化这些边及其频率,提供精确尺寸的精确测量。此外,逃逸边缘表示可能在过程扩展阶段处理的不一致性。

在上图中,为了评估模型的精度,我们认为
模型的行为包括所有日志的行为(完美拟合度)
。
2.方法思想
该方法的关键概念是逃逸边缘,即模型允许比日志更多的行为,因此显示出较低的精度。
我们的测量基于逃逸边的数量和频率之间的关系,而
逃逸边与模型的行为仅限于日志
。因此,模型越偏离日志,其精度值越低。重要的是要强调一个事实,即模型可以具有很少的逃逸边缘(因此显示出良好的精度),但其基本行为明显大于日志:本工作的目的不是比较模型和日志之间的尺寸,而是提供改进模型以精确描述日志所需的努力的估计。
为了
对模型行为进行基于日志的遍历,需要在日志和模型之间找到一个公共的可比较域,即可以映射模型状态和日志状态
。为了执行这样的任务,必须获得两个对象(模型和日志)的状态信息。在日志方面,曾提出了几种算法,将状态信息合并到日志中。这些算法可根据状态(过去、未来或两者)的决定、信息的表示(序列、集合和多集合)及其范围(有限或无限)进行参数化。特别是,使用过去、序列和无限设置可以使用相同的语言导出日志(变迁系统)的行为表示。该变迁系统的状态将是日志的状态。
2.1 前缀自动机
定义4
.(
前缀自动机Prefix automaton、日志状态
)给定事件日志EL,TS=(S,t,A,s0)是使用过去、序列和无限设置导出的自动机,称这种自动机为前缀自动机。S将表示为EL的状态集。给定轨迹σi=t1…t|σi|∈ EL,sij∈ S表示对应于前缀t1…tj的TS中的状态,0≤ j≤ |σi|+1。

下图为一个示例,该变迁系统的状态对应于日志中轨迹的前缀:例如,下图中填充的状态对应轨迹3、6和7中包含的前缀r、sb、p。

2.2 日志和Petri网的映射
为了获得Petri网模型的状态信息,可以计算其可达状态。然而,由于众所周知的空间爆炸问题,Petri网可能表现出较大甚至无限的行为,这使得这种方法在这些情况下不切实际。相反,本文中提出的方法仅访问网的可到达标记,其中日志中至少有一个状态映射了这些标记。让我们正式定义映射:
定义5(日志状态和Petri网标记之间的映射)
设EL和PN=(P,T,W,M0)分别为日志和Petri网,并考虑来自EL的前缀自动机TS=(S,T,A,s0)。如果存在一条轨迹σ使得s0->s(经过σ)并且M0[σ>M,则称一个标记 M被映射到状态s∈ S,记为M-。s。

由于这种映射,可以控制Petri网遍历以仅到达日志中有对应映射状态的标记。此外,对于在该引导遍历中到达的每个标记,局部精度可以通过收集模型中允许的行为与日志中观察到的行为之间的差异来测量该标记:
定义6(允许的任务和反映的任务)
。设s是来自EL的前缀自动机TS=(S,T,A,s0)的状态和 PN=(P,T,W,M0)。定义AT(s)={t∈ T|M-。s∧ M[t>M’}和RT(s)={t∈ T|s T→ s’}作为s中允许和反映的任务集。

由于我们假设模型中的一个适合度值是关于日志的,因此显然RT(s)⊆AT (s) 对于TS的每个状态s,即模型过接近日志。现在可以定义逃逸边缘的概念:
定义7(逃逸边缘)。设s是一个前缀自动机TS=(S,T,A,s0)的状态对于一个日志EL和 一个Petri网PN=(P,T,W,M0)。s的逃逸边缘(EE)被定义为EE(s)=AT(s)\RT(s)。

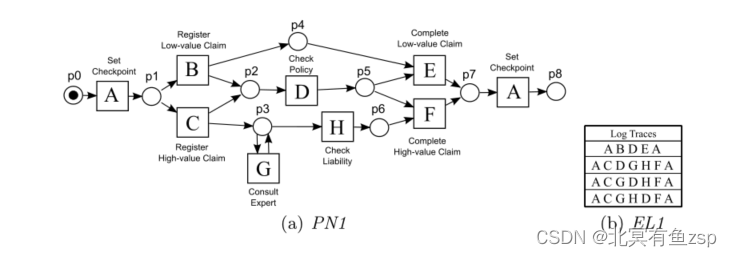
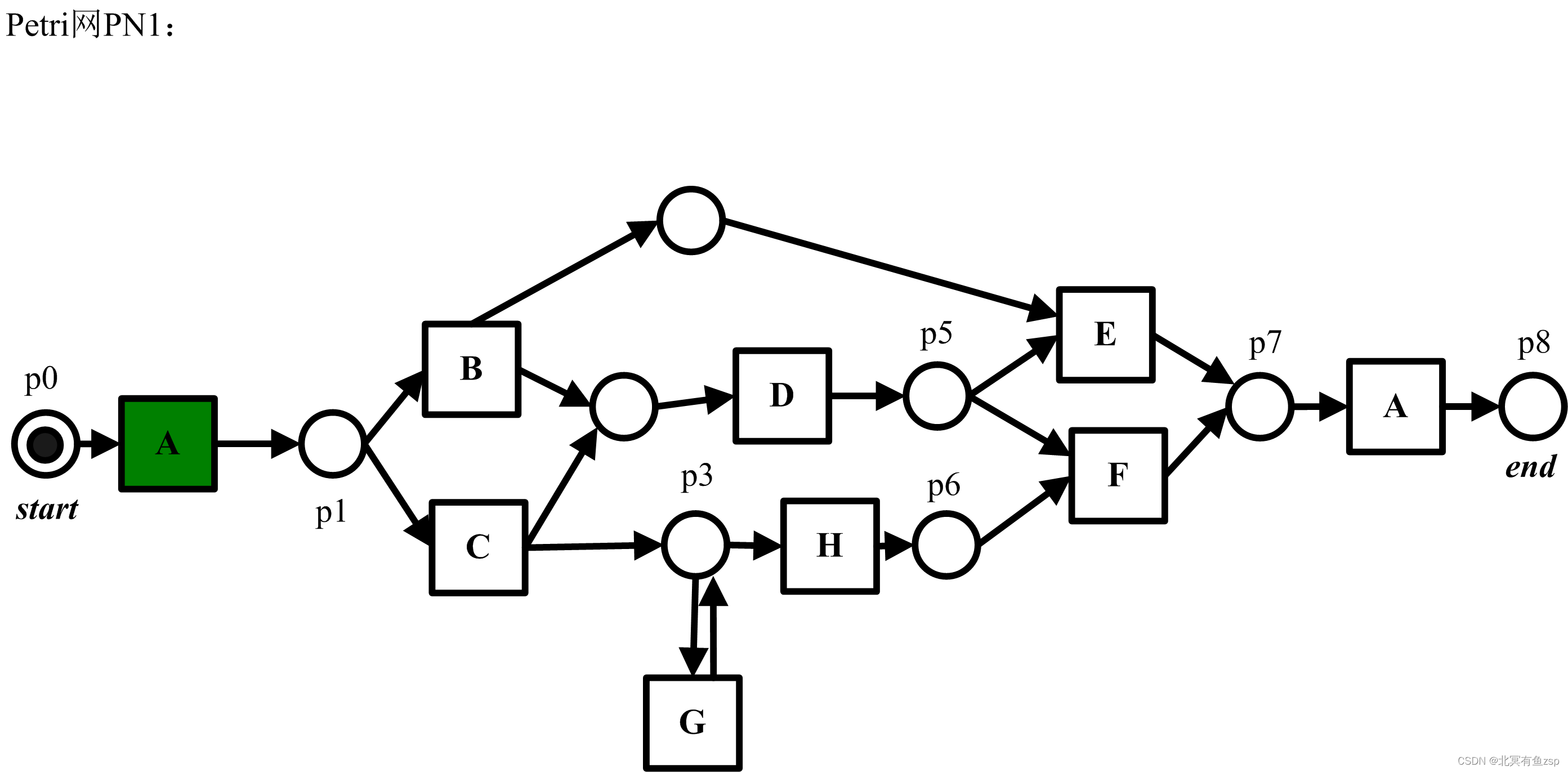
图1中的一对(PN1,EL1)的逃逸边缘的示例是在前缀AC之后达到的日志状态中的H:PN1接受H任务,而这在EL1中没有反映。重要的是要强调,状态s反映的任务是出现在包含s的任何轨迹中的任务。例如,对于图1的示例,前缀A在模型中有两个允许的任务(B和C),但假设这两个任务都反映在日志中(在不同轨迹中),在观察到A之后,在日志状态中没有出现逃逸边缘。
提出了收集逃逸边缘集合的算法如下。

2.3 ETC-precision定义
如前所述,逃逸边缘是一个很好的指标,用于测量模型的行为与日志中反映的行为相比。出于这个原因,提出了一个度量来考虑这些逃逸边缘及其频率。该度量还允许我们比较模型,以了解哪个模型更好地捕获日志所反映的行为。让我们形式化度量:
度量(ETC-precision)
设EL={σ1,…,σ|EL|}和PN=(P,T,W,M0)分别为日志和Petri网。对于每个轨迹σi(1≤ i≤ |EL|)、状态sij(1≤ j≤ |σi|+1)表示 σi中的第j个状态。度量定义如下:
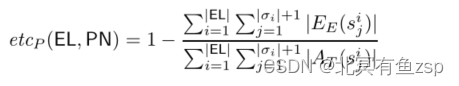

通过将逃逸边集除以模型中允许的任务集,度量评估每个轨迹中的过度近似量。注意,对于所有sij,|EE(sij)|≤ |AT(sij)|,因此0≤ etcP≤ 1.我们考虑到轨迹的频率这一事实,使得最常用和最合适的轨迹比噪声轨迹和错误的不确定选择具有更高的权重。
3.案例介绍
3.1 示例的事件日志EL1和PN1如下图所示:
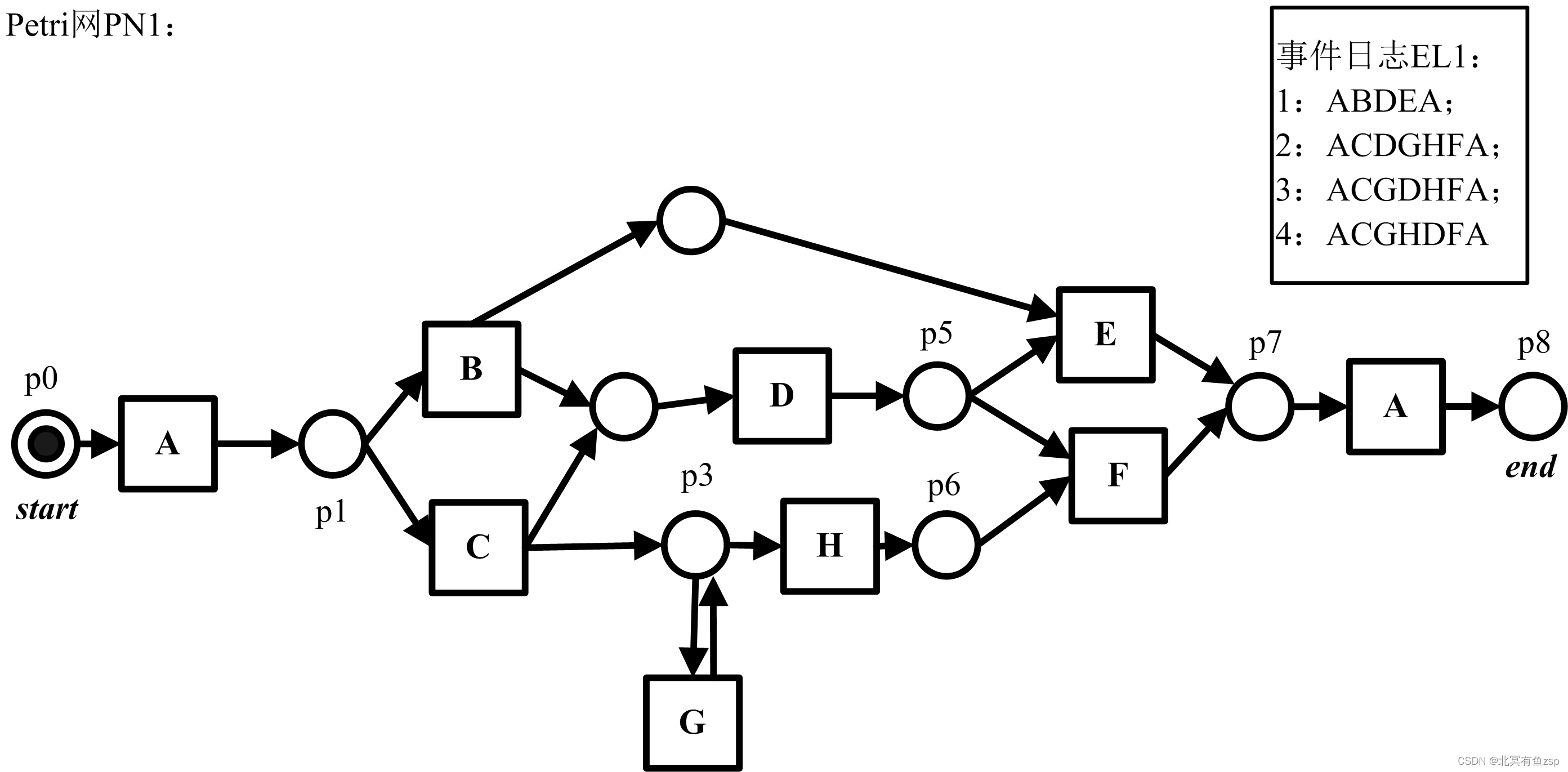
3.1 将事件日志转化为前缀自动机,如下图所示:
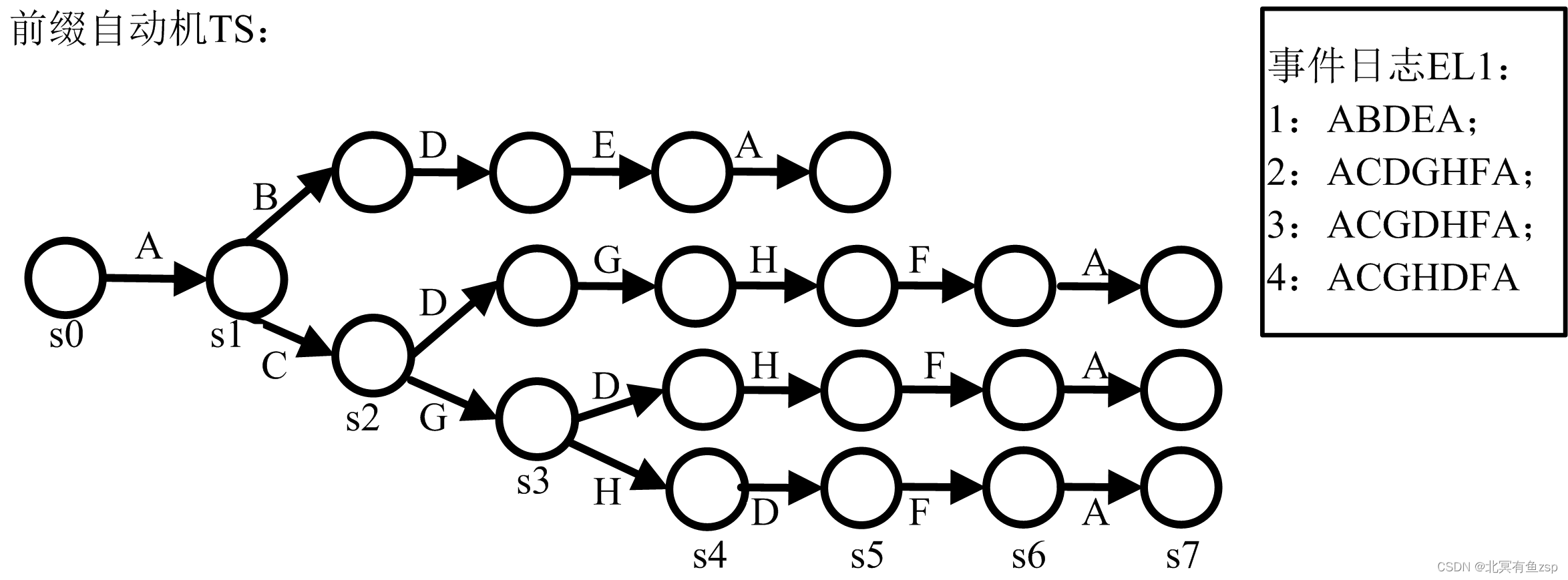
3.2 以轨迹4为例,计算其中的AT、RT、EE
(1)由于前缀自动机状态为s0时,前缀的任务为空,
, 在自动状态机上,状态s0由于能够触发A,所以此时RT={A},在Petri网上,此时经过库所p0后可以使能的变迁为A,所以此时AT={A},根据EE(
)=AT\RT(表示不在RT中的AT的集合元素),所以EE(
)=
;
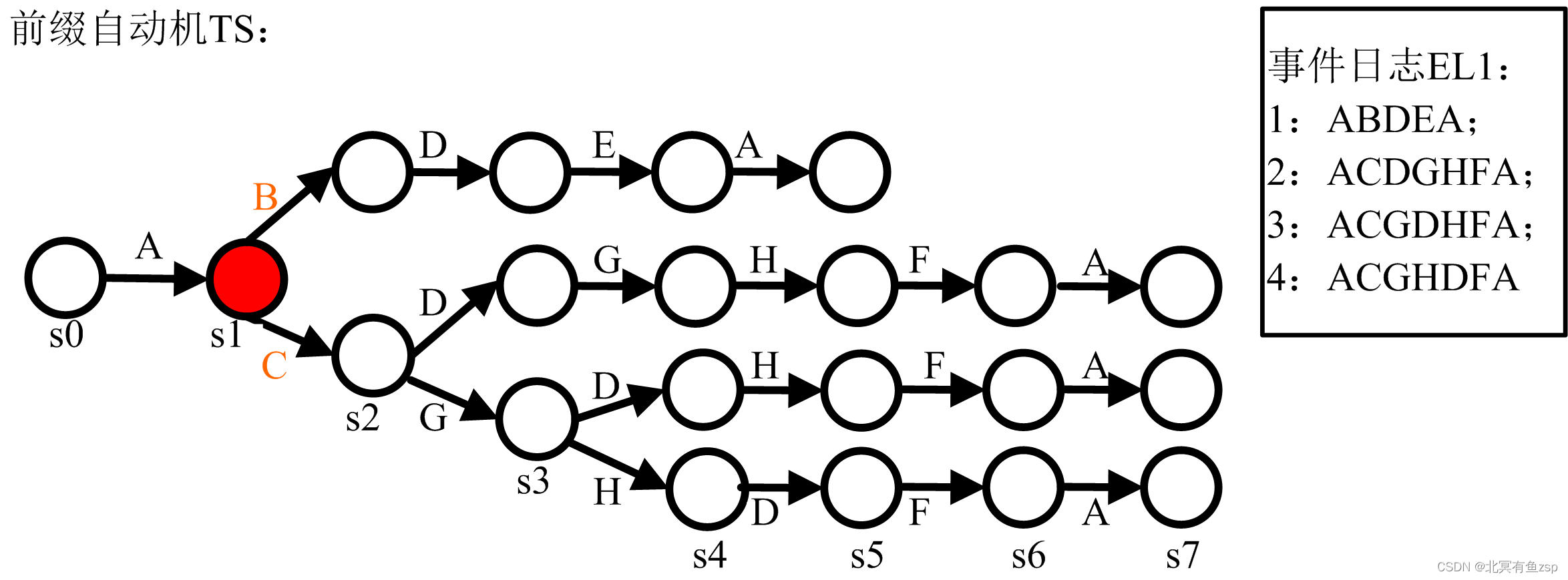
(2)从前缀自动机的状态s1开始,前缀的任务为A,所以此时
={A}。在自动状态机上,状态s1由于能够触发B和C,所以此时RT={B,C},在Petri网上,此时经过A之后可以使能的变迁为B、C,所以此时AT={B,C},根据EE(
)=AT\RT(表示不在RT中的AT的集合元素),所以EE(
)=
;

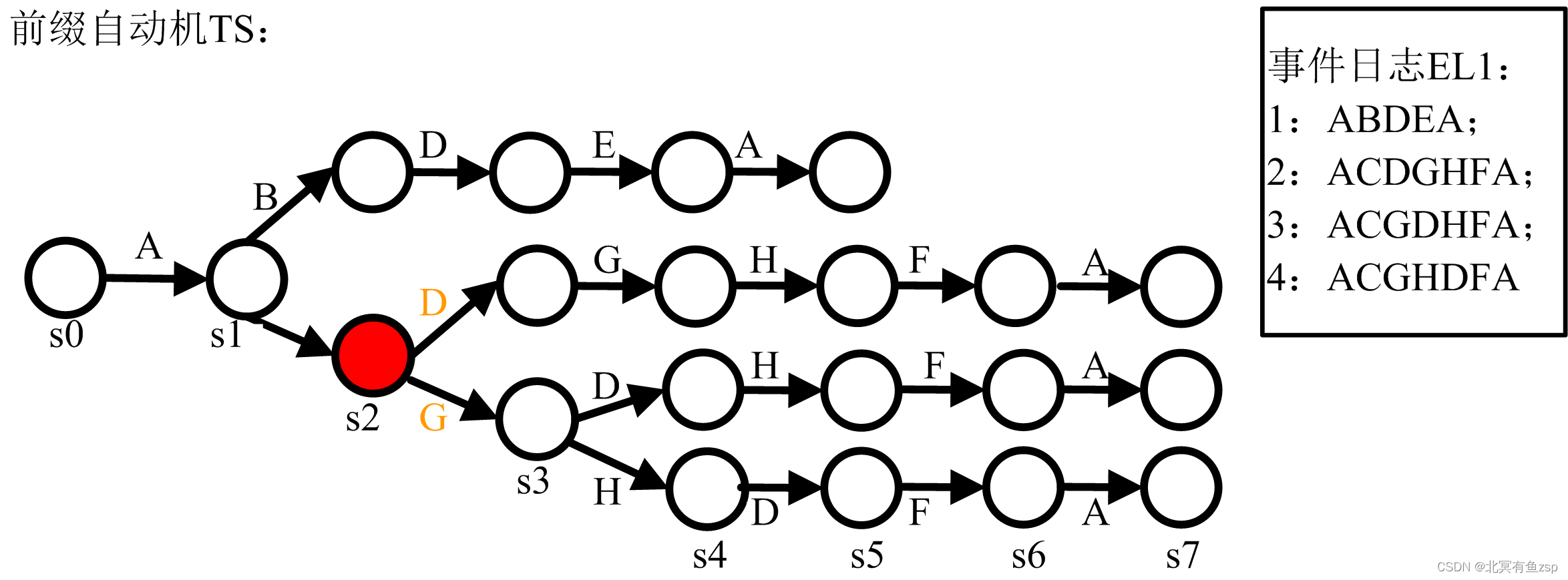
(3)当前缀自动机的状态处于s2时,此时
2为{A,C},在自动机上s2能够触发任务D和G,所以此时RT={D,G};在PN1上,此时经过A,C后,可以使能的变迁为D,H,G,所以此时AT={D,H,G},根据EE(
)=AT\RT={H};

(4)当前缀自动机的状态处于s3时,此时
3为{A,C,G},在自动机上S3能够触发任务D和H,所以此时RT={D,H};在PN1上,此时经过A,C,G后,可以使能的变迁为D,H,G,所以此时AT={D,H,G},根据EE(
)=AT\RT={G};


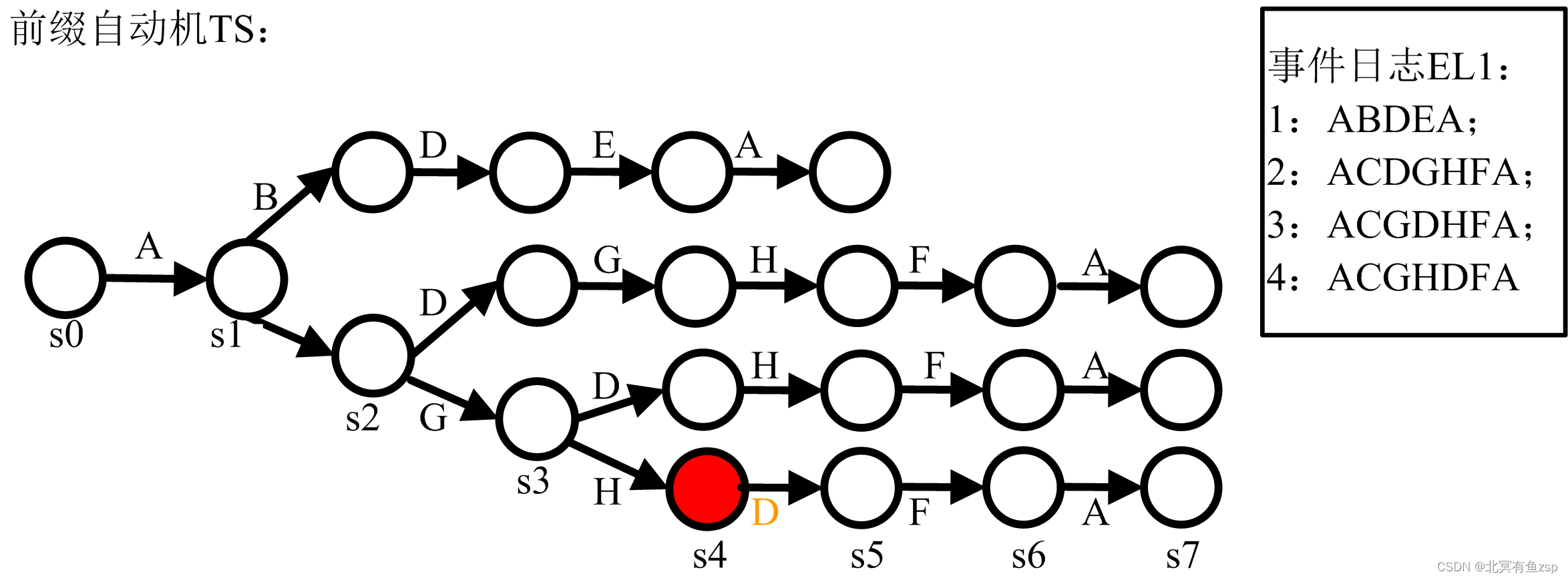
(5)当前缀自动机的状态处于s4时, 此时
4为{A,C,G,H},在自动机上s4能够触发任务D,所以此时RT={D};在PN1上,此时经过A,C,G,H后,可以使能的变迁为D,F,所以此时AT={D},根据EE(
)=AT\RT=
;
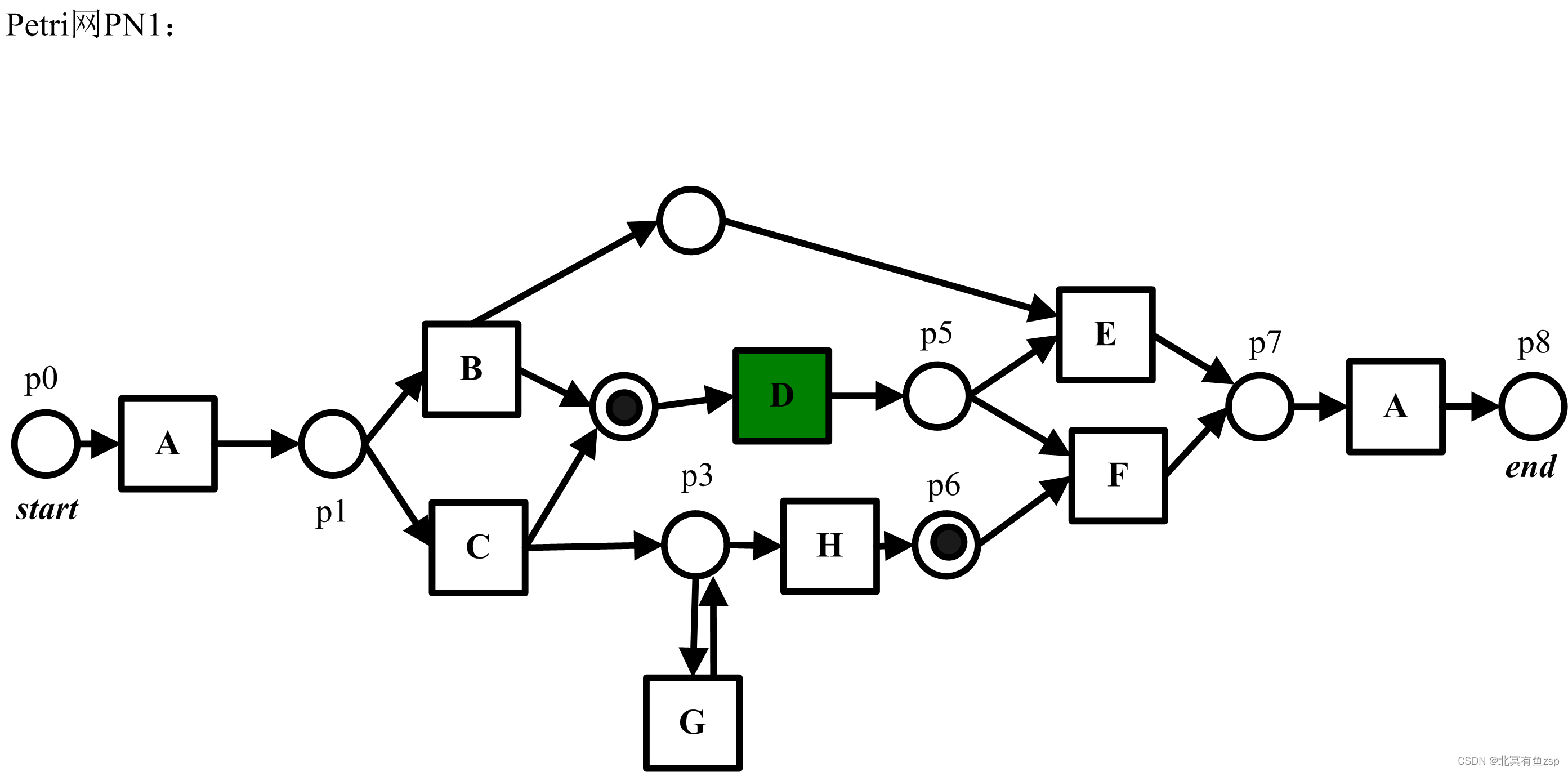
(6)当前缀自动机的状态处于s5时,此时
5为{A,C,G,H,D},在自动机上s5能够触发任务F,所以此时RT={F};在PN1上,此时经过A,C,G,H,D后,可以使能的变迁为F,所以此时AT={F},根据EE(
)=AT\RT=
;


(7)当前缀自动机的状态处于s6时,此时
6为{A,C,G,H,D,F},在自动机上s6能够触发任务A,所以此时RT={A};在PN1上,此时经过A,C,G,H,D,F后,可以使能的变迁为A,所以此时AT={A},根据EE(
)=AT\RT=
;

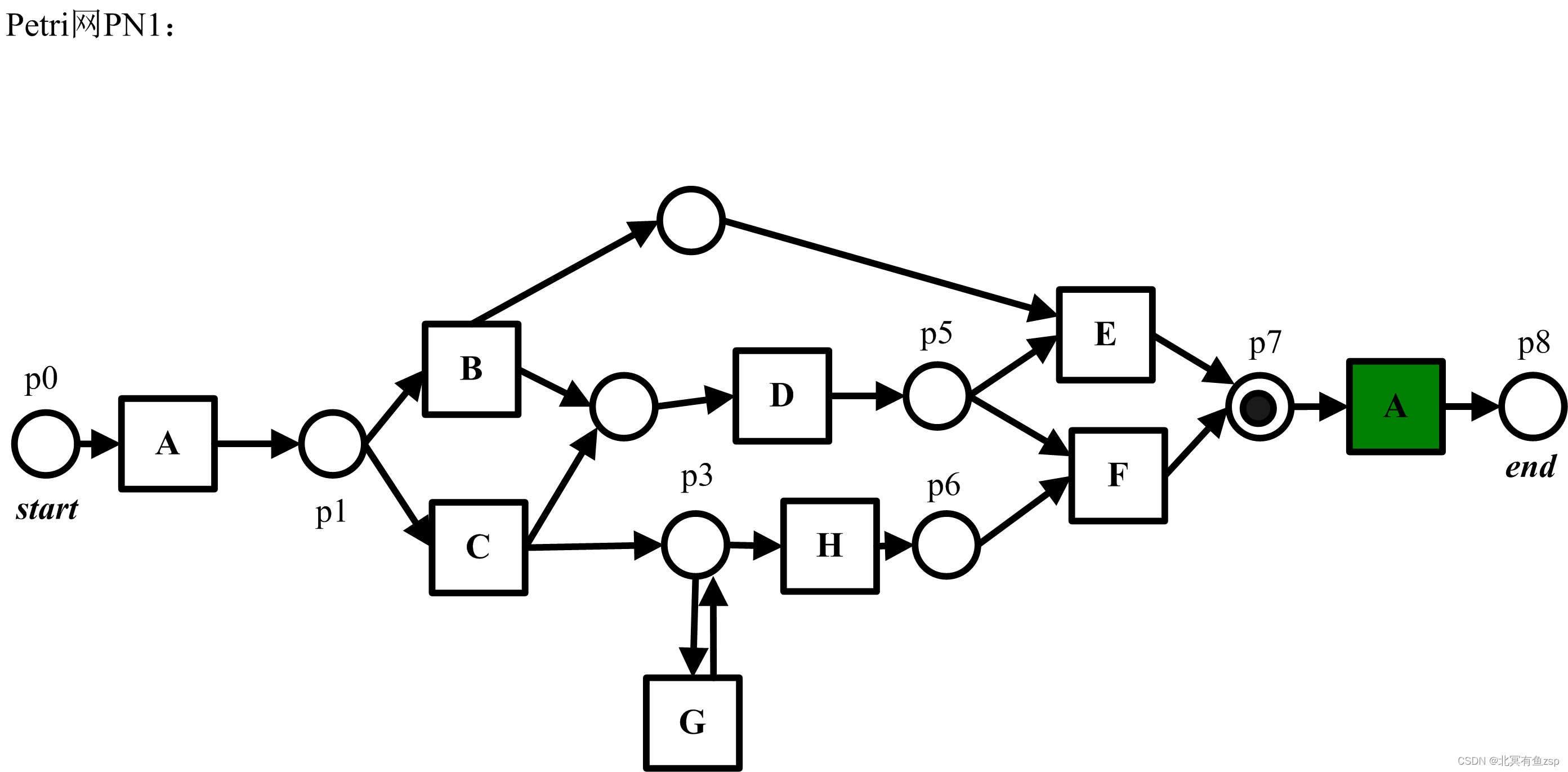
(8) 当前缀自动机的状态处于s7时,此时
7={A,C,G,H,D,F,A},在自动机上s7能够触发任务
,所以此时RT=
;在PN1上,此时经过A,C,G,H,D,F,A后,没有使能的变迁,所以此时AT=
,根据EE(
)=AT\RT=
;
经过上述步骤后,轨迹4的EE共2个, 有12个AT(1+2+3+3+1+1+1),即轨迹4有2个逃逸边缘和12个允许的任务。
3.3 事件日志EL1和PN1的精确度值计算
由1到N,可从一条轨迹推演到整个事件日志,计算公式如上述所示,所以(PN1,EL1)的示例的度量值为:
其中,分子/分母的每一个第i个和都在处理轨迹σi的逃逸边惩罚,例如轨迹σ4∈ EL1有2个逃逸边缘和12个允许的任务。
4.工具实现
该方法已作为插件在ProM 中实现,插件名为“Check Conformance using ETConformance”。


5.总结
这是一种低复杂度技术,允许检查一般Petri网相对于日志的精度。通过只关注反映在日志中的Petri网的底层行为,该技术避免了在处理大型高并发网络时可能出现的潜在状态爆炸。该理论已作为ProM 6中的插件实现。
下一讲我们将介绍基于对齐(Alignment)的重演技术-precision。
1.Munoz-Gama J, Carmona J. A fresh look at precision in process conformance[C]//International Conference on Business Process Management. Springer, Berlin, Heidelberg, 2010: 211-226.