遗传算法是一个非常经典的智能算法,主要用于解决优化问题。本文主要简单介绍一些原理,同时给出一个基于python实现的,用于解决实数内优化问题的模板。
本文参考:
原理:
遗传算法入门详解 – 知乎
简单介绍
遗传算法就是借鉴生物学中的遗传,首先生成若干种群,内有一些个体,也就是解,对不同解设定适应度,采用算子产生新解,不断在种群内遗传优秀基因,最终达到优化的目的。
所以最终一定有若干个群体
,内部的个体都是比较优秀的,不优秀的就被淘汰了。
相关概念
下面主要是一些基本的概念,参考了上面提到的链接部分,只是摘取了部分并作了一些注解,详细的可以自行去了解。
① 染色体(Chromosome):
染色体又可称为基因型个体(individuals),一定数量的个体组成了群体(population),群体中个体的数量叫做群体大小(population size)。
② 位串(Bit String):
个体的表示形式。对应于遗传学中的染色体。
③ 基因(Gene):
基因是染色体中的元素,用于表示个体的特征。例如有一个串(即染色体)S=1011,则其中的1,0,1,1这4个元素分别称为基因。
④ 特征值( Feature):
在用串表示整数时,基因的特征值与二进制数的权一致;例如在串 S=1011 中,基因位置3中的1,它的基因特征值为2;基因位置1中的1,它的基因特征值为8。
⑤ 适应度(Fitness):
各个个体对环境的适应程度叫做适应度(fitness)。为了体现染色体的适应能力,引入了对问题中的每一个染色体都能进行度量的函数,叫适应度函数。这个函数通常会被用来计算个体在群体中被使用的概率。
⑥ 基因型(Genotype):
或称遗传型,是指基因组定义遗传特征和表现。对于于GA中的位串。
⑦ 表现型(Phenotype):
生物体的基因型在特定环境下的表现特征。对应于GA中的位串解码后的参数。
染色体就是一个个体,在具体的计算中就是n维空间内的一个解
位串也就是一个个体的编码后的样子
基因也就是染色体上面所包含的特征,也就是编码后的一位
特征值表示这个位在这个编码规则下的含义
适应度表示在计算过程中被使用的概率,一般是解的优质情况
基因型表示编码后的字符串
表现型表示解码后的参数
遗传步骤
-
编码和解码的规则
两个过程是逆过程,编码就是把一个解编成一个序列,一般采用
二进制编码
,解码就是反过来。 -
生成初始值
这个过程就是生成需要的变量
设置最大进化代数 T ,群体大小 M ,交叉概率 Pc ,变异概率 Pm ,随机生成 M 个个体作为初始化群体 P0
-
改变适应度
主要用于改变每个个体的适应度,防止适应度相当,然后就没什么优胜劣汰了。
一般来讲,是指算法迭代的不同阶段,能够通过适当改变个体的适应度大小,进而避免群体间适应度相当而造成的竞争减弱,导致种群收敛于局部最优解。
有很多方式,线性非线性…
-
遗传算子
-
选择
选择就是在一个旧种群内(包含多个个体)内选择优良的种群,并在其中选择优良的个体进行繁殖,可以达到优生优育。
常用
轮盘赌
,也就是个体选择概率为个体的的适应度除以群体的总适应度,适应度高,被选择概率大,可以得到优秀后代。 -
交叉
交叉就是两个染色体之间产生一些交换,从而完成产生新解的操作,常用
单点交叉
,还有其他… -
变异
变异就是自身有一定概率发生改变,比如变了一位二进制,也产生了新解。
-
这个过程有三种,主要就是用于生成新的解,把不同的解放到一起或者自己生成新解, 同时这
几个过程也有多种方式呈现
,并不一定拘泥于提到的,针对不同问题也会有不同的解 决方案。
注意点
遗传算法y一般有4个运行参数需要预先设定,即
M :种群大小
T :遗传算法的终止进化代数
Pc :交叉概率,一般为0.4~0.99
Pm :变异概率,一般取0.001~0.1
代码实现
下面是具体的代码实现,我采用的编码方式就是
直接生成浮点数
,选择操作每次
保留设定比例
的个体,交叉操作每次
选择两组参数以一定概率进行参数调换
,产生新个体,变异操作
对每个值以一定概率对某个参数进行重新取值
,模拟变异操作。
记录的参数有三组,分别是每一轮的最优适应度,最优结果和对应的最优参数,最终画图。
代码
import warnings
from math import log2
import matplotlib.pyplot as plt
import pandas as pd
warnings.filterwarnings('ignore')
import heapq
import itertools
from random import randint, random, uniform
import numpy as np
def select_op(fitness,op,select_rate,best_keep_rate):
ans_list = []
# 先选择保留部分
keep_num = int(best_keep_rate * len(op)*select_rate)
index_list = list(map(list(fitness).index, heapq.nlargest(keep_num, fitness)))
for index in index_list:
ans_list.append(op[index])
# 保留的
p =fitness/sum(fitness) # 计算每个个体占比
p = np.array(list(itertools.accumulate(p))) # 计算累积密度函数
# 采用轮盘赌方式选择
for i in range(int(len(op)*select_rate)-keep_num): # 再产生这么多个
r = random()
index = np.argmax(p>r) # 找到第一个大于随机的值
if index == 0 and p[0] < r: # 可能第一个并不大于这个数,可能是没找到,也是返回0
continue
ans_list.append(op[index])
return ans_list
def cross_op(op,cross_rate,num):
ans_list = []
num_op = len(op) # 当前数量
while num > 0:
max_ = 5 # 最多找5次,如还是相同就用相同的,就说明这个基因很多
while max_>0:
n1 = randint(0,num_op-1)
n2 = randint(0,num_op-1) # 不允许相同个体杂交
max_ -= 1
if op[n1] != op[n2]:
break
father = op[n1]
mother = op[n2]
if random() < cross_rate:
location = randint(0,len(father)-1) # 随机产生交叉位置
tmp = father[0:location+1] + mother[location+1:len(father)]
ans_list.append(tmp)
num -= 1
return ans_list
def variation_op_10(new_op,variation_rate,low,high):
for index,it in enumerate(new_op): # 一定概率变异
if random() < variation_rate:
location = randint(0, len(it) - 1)
it = uniform(low[location],high[location]) # 随机产生数字
new_op[index][location] = it
return new_op
# 生成随机初始值
def ini_op(low_paras, high_paras, max_op_size):
# 计算出每个参数应该占的位数
st = 0
ed = -1 # 为了保证st为-1
para_range = []
for i in range(len(low_paras)):
low_it = low_paras[i]
high_it = high_paras[i]
num = int(log2(high_it - low_it + 1)) + 1 # 计算二进制位数
st = ed + 1
ed += num
para_range.append((st, ed)) # 加入每个参数的范围,包括起始点和终点(在序列中的)
op = []
for i in range(max_op_size):
tmp = [uniform(low_paras[k], high_paras[k]) for k in range(len(low_paras))]
op.append(tmp)
return op, para_range
def cal_fitness(op):
ans_list = np.zeros((len(op), 1))
for index, it in enumerate(op): # 取出每个参数对应的数字
if un_suit(it): # 如果不满足约束条件
ans_list[index] = 1000000000 # 给一个很大的值,最后要统一处理
continue
y = func(it)
ans_list[index] = y
ans_list = func_fitness(ans_list)
return ans_list
# 自定义适应度函数计算
def func_fitness(ans_list):
if model_dir == 'min':
for index, it in enumerate(ans_list):
ans_list[index] = 1 / it
return ans_list
def un_suit(x): # 定义参数不满足的约束条件
# 参数范围约束
for i in range(len(low_paras)):
if x[i] < low_paras[i] or x[i] > high_paras[i]:
return True
# ...自行添加
return False
# 定义计算函数
def func(x):
return x[0] ** 2 + x[1] ** (3 / 2) + x[2] + x[3] ** (1 / 2)
# ---配置参数
paras_name = ['x1', 'x2', 'x3', 'x4']
high_paras = [60,60,40,30] # 参数范围上限
low_paras = [10, 21,3,10] # 参数范围下限
model_dir = 'min' # max表示越大越好,min表示越小越好
# ---配置遗传算法参数
max_op_size = 200 # 种群大小,这里也是考虑一个种群的优化问题
max_epochs = 200 # 迭代次数,也就是进化次数
cross_rate = 0.8 # 杂交率,选出两个个体之后以这个概率杂交(各取部分基因产生后代)
select_rate = 0.4 # 选择率,也就是选择保留占总的个数(这里实际是利用随机数抽取,而不是按照排序)
variation_rate = 0.1 # 变异率,产生新的个体以这个概率变异(一位重新赋值)
best_keep_rate = 0.1 # 每次选择必定保留的比例(排序靠前的部分)
# ---遗传算法求解
if __name__ == '__main__':
data = np.array(pd.read_excel('../static/test.xlsx')) # 读入数据
op, para_range = ini_op(low_paras, high_paras, max_op_size) # 初始化种群,返回种群和每个参数的位置范围[(l1,r1),(l2,r2)...]
best_ans_history = [] # 记录最优答案历史
best_para_history = [] # 记录最优对应参数
best_fitness_history = [] # 记录最优适应度
for i in range(1, max_epochs + 1):
if i % 50 == 0:
print('epoch:', i)
# 计算适应度
fitness = cal_fitness(op) # 计算适应度
index = np.argmax(np.array(fitness)) # 为什么已经保留了最佳适应度,最后的图还是会上下跳动
best_fitness_history.append(fitness[index])
best_para_history.append(op[index])
best_ans_history.append(func(op[index]))
op = select_op(fitness, op, select_rate, best_keep_rate) # 选择个体,选择比例为
# 交叉,产生后代
new_op = cross_op(op, cross_rate, max_op_size - len(op)) # 后一个参数为需要产生的个数
# 变异
new_op = variation_op_10(new_op, variation_rate,low_paras,high_paras) # 变异
op.extend(new_op) # 把新的个体加入群落
plt.rcParams['font.sans-serif'] = ['SimHei'] # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False # 用来正常显示负号
index = np.argmax(best_ans_history)
print('最优结果为:', best_ans_history[index])
print('最优参数如下')
for name,index in zip(paras_name,best_para_history[index]):
print('{}={}'.format(name,index))
plt.plot(best_fitness_history, label='适应度曲线变化')
plt.legend()
plt.show()
example
就以一个单调函数为例:
x1 ** 2 + x2 ** (3 / 2) + x3 + x4 ** (1 / 2)
设定范围如下:
high_paras = [60,60,40,30] # 参数范围上限
low_paras = [10, 21,3,10] # 参数范围下限迭代两百轮停止,输出结果
最优结果为: 262.08470155055244
最优参数如下
x1=10.92155546612619
x2=22.81339324058242
x3=30.588146368196167
x4=10.573758934746433
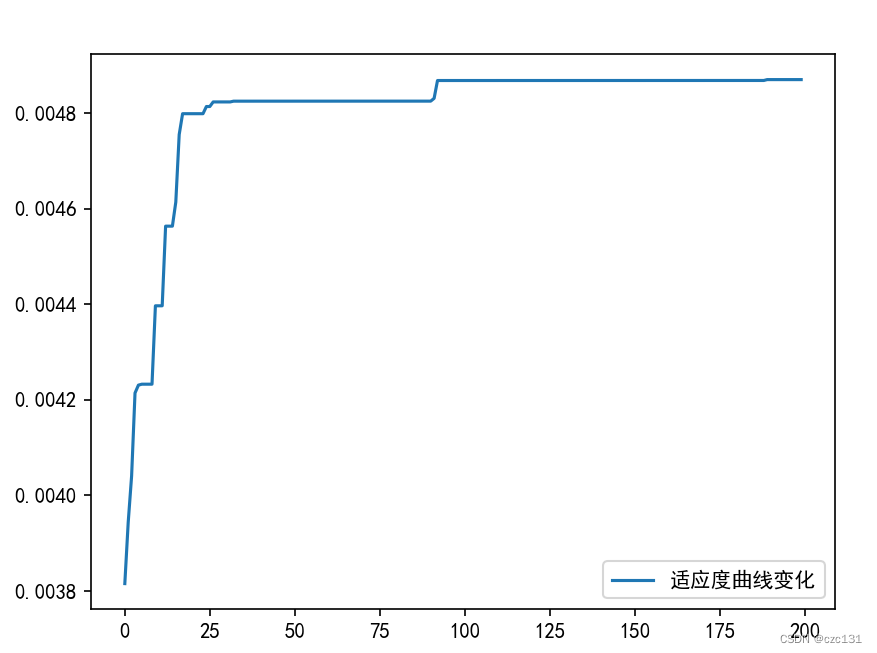
输出最优适应度变化曲线: