平方序列

是很简单的枚举,但是为了简化,也需要注意一些技巧
1.并不需要两层枚举去试x,y,我们只需要从比2019大的第一个数2020开始枚举x的值,然后根据2019和x的值算一下y2
2.算出y2后,一开始写错成了sqrt(y2)>x,就输出答案
正确的做法是,如果sqrt(y)是整数,才输出答案
怎么判断y是整数?先算出y2的平方根,再把平方根平方,看是否等于原来的y2
#include<iostream>
#include<math.h>
using namespace std;
int main(){
int x,y,t; //t代表x取每个值时的y2
for(x=2020;;x++){
//构成等差数列,则x2-2019 2=y2-x2
t=x*x+(x*x-2019*2019);
y=sqrt(t);
if(y*y==t){
cout<<x+y<<endl;
return 0;
}
}
}
质数拆分

首先先复习一下欧拉筛法
bool isprime[100]; //isP[i]表示i是不是素数
int prime[100]; //已经筛出的素数列表
int n; //筛出<=n的素数
int cnt; //已经筛出的素数个数
void euler(){
memset(isprime,true,sizeof(isprime));
isprime[1]=false; //1不是素数~~
for(int i=2;i<=n;i++){
if(isprime[i])
prime[++cnt]=i; //如果i没有被前面的数筛掉,则i是素数
for(int j=1;j<=cnt && i*prime[j]<=n;j++){
//筛掉i的素数倍,也就是i的prime[j]倍
//j循环枚举现在已经筛出的素数
isprime[i*prime[j]]=false;
//把prime[j]代表的这个素数的i倍筛掉
if(i%prime[j]==0)break;
//这句话是关键点所在~~~~这样可以保证线性的时间复杂度
}
}
}本道题的核心思想是:先用欧拉筛法把素数筛出来,存在pre数组中
dp[i][pre[j]]表示满足这些额外条件的分解方案数:
1、被分解数为i
2.分解出的素数最大值恰好为pre[j]
那么状态转移方程就是
for(int k=0;k<j&&pre[k]<=i-pre[j];k++)
dp[i][pre[j]]+=dp[i-pre[j]][pre[k]]
#include<cstdio>
#include<cstdlib>
#include<iostream>
#include<algorithm>
using namespace std;
typedef long long ll;
const int N=1e4+20;
const int M=2019;
int pre[N],cnt;
bool vis[N];
ll dp[N][N];
void euler()
{
for(int i=2;i<N-10;i++)
{
if(!vis[i])
pre[cnt++]=i;
for(int j=0;j<cnt&&i*pre[j]<N-5;j++)
{
vis[i*pre[j]]=1;
if(i%pre[j]==0)break;
}
}
}
int main()
{
euler();
for(int i=0;pre[i]<=M;i++)
dp[pre[i]][pre[i]]=1;
for(int i=2;i<=M;i++)
{
for(int j=0;pre[j]<=i;j++)
{
for(int k=0;k<j&&pre[k]<=i-pre[j];k++)
dp[i][pre[j]]+=dp[i-pre[j]][pre[k]];
}
}
ll ans=0;
for(int i=0;pre[i]<=M;i++)
ans+=dp[M][pre[i]];
cout<<ans<<endl;
return 0;
}
答案:55965365465060
求值

这道题问的其实就是,含有100个约数的最小数是啥
答案:45360
非常非常简单的暴力找一下
#include<iostream>
using namespace std;
int main()
{
for(int i=1;;i++){
int sum=0;
for(int j=1;j<=i;j++){
if(i%j==0)
sum++;
}
if(sum==100){
cout<<i<<endl;
break;
}
}
}
路径计数

这道题是很经典的dfs走迷宫!~
答案:206
#include<iostream>
using namespace std;
//因为路径不自交,一定有一个vis数组(其实就是不走回头路)
bool vis[10][10];
//上下左右用这两个数组来试探
int dx[4]={0,0,1,-1};
int dy[4]={1,-1,0,0};
int ans;
//x,y是当前走到的位置,这道题的剪枝就在于不走超过12步,那么再有一个k来记录走过的路
void dfs(int x,int y,int k){
if(k>12)
return; //剪枝!
for(int i=0;i<4;i++){
int tx=x+dx[i];
int ty=y+dy[i]; //tx,ty是在这一步试探中,要走向的格子
if(tx==0 && ty==0 && k+1>2 && k+1<=12)
ans++; //如果走回了(0,0),且走的步数>1(不是待在起点),且走了这不不超过12,路径方案+1
if(tx<0 || tx>7 || ty<0 || ty>7)continue; //已出界
if(vis[tx][ty])continue; //路径自交了
//接下来才到了“迈出这一步”的环节
//经典的三行代码:
vis[tx][ty]=true;
dfs(tx,ty,k+1);
vis[tx][ty]=0;
}
}
int main()
{
vis[0][0]=true; //一开始把0,0标记为走过了,所以要注意一下dfs函数里if的先后,如果先判断有没有走过,那就永远都走不到终点啦
dfs(0,0,0);
cout<<ans;
}
最优包含
思路:
涉及字符串,本题也使用动态规划
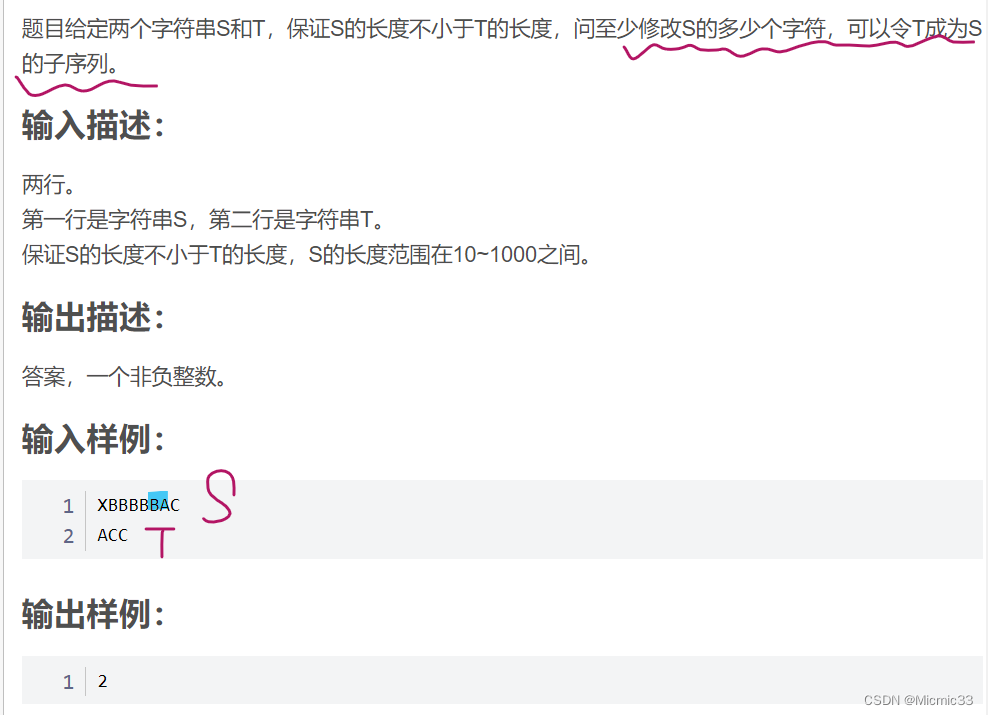
T是较短的那个串,问至少S中改几个,T能成为S的子串
我们设dp[i][j]表示S串中前i个字符,包含有T串中前j个字符最少需要修改的字符个数。
因此分析得到:
如果S[i]=T[j] ,那么T串中的最后一位要么让他和S[i]相等,要么让他和前面的相等。
dp[i][j] = min(dp[i-1][j],dp[i-1][j-1]);
如果S[i]!=T[j],那么要么是让T[j]和S串前面的字符一样,要么修改S[i]。
dp[i][j]= min(dp[i-1][j-1]+1,dp[i-1][j])
并且注意的是这里动态方程中我们的i,j为个数的意思,转换为代码时由于下标从0开始,所以实际上要大一
#include<iostream>
#include<string>
#include<string.h>
using namespace std;
const int N=1e3+50;
string a,b;
int dp[N][N];
int main(){
cin>>a>>b;
int la=a.size();
int lb=b.size();
memset(dp,0x3f3f3f3f,sizeof dp);
dp[0][0]=0;
for(int i=1;i<=la;i++)
{
dp[i][0]=0;
for(int j=1;j<=lb;j++)
{
if(a[i]==b[j])
dp[i][j]=min(dp[i-1][j],dp[i-1][j-1]);
else
dp[i][j]=min(dp[i-1][j],dp[i-1][j-1]+1);
}
}
cout<<dp[la][lb];
return 0;
}
排列数
对于一个数列中的某个数,如果这个数
比两侧的数都大
或
比两侧的数都小
,我们称这个数为这个数列的一个转折点。
如果一个数列有t个转折点,我们称这个数列为t+1调数列。
给定两个正整数n,k。求在1~n的全排列中,有多少个数列是k调数列。
用的是没有啥优化的库函数。。
#include<iostream>
#include<string>
#include<algorithm>
#include<string.h>
using namespace std;
int n,k; //有k-1个转折点,n个数
int cnt;
int a[100005];
int main(){
cin>>n>>k;
for(int i=0;i<n;i++)
a[i]=i+1;
do{ int num=0;
for(int i=1;i<n-1;i++){
if( (a[i]>a[i-1] && a[i]>a[i+1] ) || (a[i]<a[i-1] && a[i]<a[i+1]))
num++;
}
if(num==k-1)
cnt++;
} while(next_permutation(a,a+n));
cout<<cnt;
}