找
张量积
概念的时候,被各种野路子博客引入的各种“积”搞混了,下面仅以Wikipedia为标准记录各种积的概念。
点积(Dot product)
https://en.wikipedia.org/wiki/Dot_product
在数学中,点积(Dot product)或标量积(scalar product)是一种代数运算,它取两个
相等长度的数字序列
(通常是坐标向量),并返回一个数字。在欧几里得几何中,两个向量的笛卡尔坐标的点积被广泛使用。
它通常被称为欧几里得空间的内积
(Inner product),或很少地被称为投影积(Projection product),尽管
它不是唯一可以在欧几里得空间上定义的内积
。
也就是说,
点积是我们通常讨论的欧氏空间中内积的一种特殊形式
。点积定义如下:
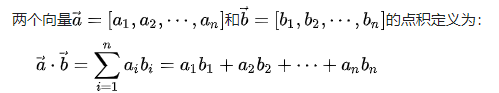
内积(Inner product)
https://en.wikipedia.org/wiki/Inner_product_space
在数学中,内积空间(少部分人称为豪斯多夫-前希尔伯特空间)是实向量空间或具有称为内积的运算的复向量空间。空间中两个向量的内积是标量,通常用尖括号表示,如$<a,b>$。内积允许对直观的几何概念进行形式化定义,例如向量的长度、角度和正交性(零内积)。内积空间推广了欧几里得向量空间,其中内积是笛卡尔坐标的点积或标量积。无穷维内积空间在泛函分析中得到了广泛的应用。复数域上的内积空间有时被称为酉空间。1898年,Giuseppe Peano首次使用了具有内积的向量空间概念。
内积的定义比较抽象,在此仅对各种积进行区分,不对定义进行记录。它甚至没有单独的词条,是和内积空间放在一起介绍的。在
工科的讨论范围内,内积和点积会混在一起说
。这是无可厚非的,毕竟点积是内积的一种特殊形式。
外积(Outer product)
https://en.wikipedia.org/wiki/Outer_product
在线性代数中,两个坐标向量的外积(Outer product)是一个矩阵。如果这两个向量的维数分别为n和m,那么它们的外积是一个n×m矩阵。更一般地说,给定两个张量(多维数组),它们的外积是张量。张量的外积也被称为它们的张量积,可以用来定义张量代数。向量外积定义如下:

叉积(Cross product,叉乘)
https://en.wikipedia.org/wiki/Cross_product
在数学中,叉积(Cross product)或向量积(Vector product)是在三维欧几里得向量空间中对两个向量的二元运算,用符号表示$\times$。给定两个线性无关的向量$a$和$b$,叉积$a×b$是一个垂直于$a$和$b$的向量,因此垂直于包含它们的平面。它在数学、物理、工程和计算机编程中有许多应用。不应将其与点积(投影积),特别是
外积
混淆。
国内总会把叉积和外积混为一谈,即使是中文维基百科也是如此。英文环境里根本就没有把cross product和outer product混在一起说的情况。叉积仅仅定义在三维的欧氏空间中,且需要用到右手定则。
张量积(Tensor product)
https://en.wikipedia.org/wiki/Tensor_product
https://www.math3ma.com/blog/the-tensor-product-demystified
就是外积在张量上的拓展。