这是一篇写得比较久的文章,前前后后三个星期。
该题的输入数据描述比较绕,反复读了几次,才明白,每行的数据描述的是一根树枝的信息,
每行的前两个数据,代表该数值的端点,第三个数据,代表该树枝上的苹果数量。
可以将苹果挂在树的节点上,这样题意更清晰,样例对应的图如下:

从暴力角度想了想,如下情况苹果树,先删那根枝呢?

确实难办,该题还是有特定算法的。
还是回归本题的表述吧。

树的拼接。
f[2][0]=0,f[5][0]=0,f[4][0]=0
f[3][0]=0,f[3][1]=max(f[3][0]+f[2][0]+20,f[3][0]+f[5][0]+20)=max(20,20)=20
f[3][2]=max(f[3][1]+f[2][0]+20,f[3][1]+f[5][0]+20)=40//f[3][1] 是确定的,那f[3][2]也就是确定的,还需要枚举?
枚举挺复杂的
枝的选取是有序的,被选择的枝,下一次是不会再被选择了,这也是01背包算法的特征。
模拟是理解算法的关键。
对01背包空间降维,逆向处理有问题,可看,若无问题,可跳过这段。
这部分是关于01背包的数据生成过程,若对01背包有疑惑,读者可以独自进行模拟,以下过程仅代表作者的模拟过程,不要求读者看懂。

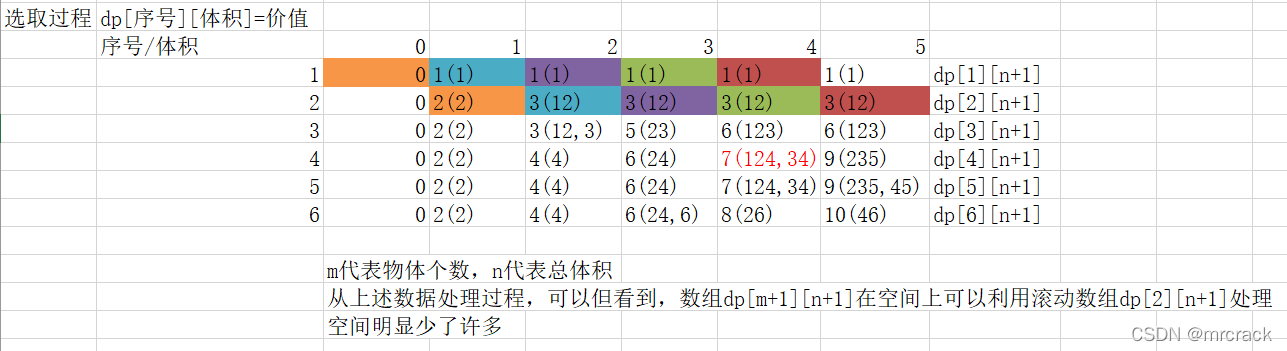


更详细的01背包深入说明:
点击这里
01背包无问题,可从此处看起。
树深搜的特征,必须搜到底,到底之后,自底向上开始运作,开始做事,换句话说,搜索是从根开始,但是具体做实事,是从叶子节点开始,自叶子节点开始向根开始做具体的实事。
sz[u]表示u的子树上的边数,可以通过计算u的子节点数量得到,请看样例中1的子节点数量是4,子树上的边数也是4。
设f[u][j]表示u的子树上保留j条边,至多保留的苹果数目
那么状态转移方程也就显而易见了
f[u][i]=max(f[u][i],f[u][i-j-1]+f[v][j]+e[i].w)
f[u][j]=max(f[u][j],f[u][j-k-1]+f[v][k]+e[i].w) ( 1≤j≤min(q,sz[u]),0≤k≤min(sz[v],j−1) )
u表示当前节点,v是u的一个子节点,sz[u]表示u的子树上的边数,q就是题目中要求的最多保留边数
那么为什么是这个方程呢?
首先,为什么是f[u][j-k-1]而不是f[u][j-k]?
为前文提到了,保留一条边必须保留从根节点到这条边路径上的所有边,那么如果你想从u的子节点v的子树上留边的话,也要留下u,v之间的连边
那么取值范围k为什么要小于等于j−1而不是j呢?
同上,因为要保留u,v连边
对了,别忘了i,j要倒序枚举(数组少开了一维)因为这是01背包
考虑用有向图应也能编写成功。在编写有向图中,不成功,重新看了看输入数据,发现,给出的数
请注意,如下的输入数据1与输入数据2描述的是同一棵树,
这两组数据最大的差别在于
2 3 20
3 2 20
正式因为这种差别,该题不能用有向图来存储数据。
输入数据1:
5 2
1 3 1
1 4 10
2 3 20
3 5 18
输出数据1:
21
输入数据2:
5 2
1 3 1
1 4 10
3 2 20
3 5 18
输出数据2:
21
据,并没有严格的指向叶节点,或叶节点指向某个点,故
有向图编写无法成功
。
1.
树的深搜遍历(深搜到叶节点,返回根节点),树的子节点数量求法(树的子树边数求法),降维的01背包,无向图。
ybt
通过
| 测试点 | 结果 | 内存 | 时间 |
| 测试点1 |
答案正确 |
616KB | 1MS |
| 测试点2 |
答案正确 |
628KB | 2MS |
| 测试点3 |
答案正确 |
628KB | 1MS |
| 测试点4 |
答案正确 |
648KB | 1MS |
| 测试点5 |
答案正确 |
660KB | 2MS |
| 测试点6 |
答案正确 |
660KB | 2MS |
| 测试点7 |
答案正确 |
664KB | 1MS |
| 测试点8 |
答案正确 |
676KB | 1MS |
| 测试点9 |
答案正确 |
680KB | 2MS |
| 测试点10 |
答案正确 |
704KB | 2MS |
| 测试点11 |
答案正确 |
696KB | 1MS |
| 测试点12 |
答案正确 |
696KB | 2MS |
| 测试点13 |
答案正确 |
704KB | 2MS |
LOJ

LUOGU


AC代码如下:
#include <bits/stdc++.h>
#define maxn 110
using namespace std;
int f[maxn][maxn];
struct node{
int to,w,next;//to表示终点,w表示权重,next表示下一条边
}e[maxn<<1];
int head[maxn],tot,sz[maxn],q;//sz[u]统计以u为父节点的树枝数量
void add(int u,int v,int w){//有段日子没编了,不过好歹通过数据模拟,想了起来。
tot++,e[tot].to=v,e[tot].w=w,e[tot].next=head[u],head[u]=tot;
}
void dfs(int u,int fa){//fa父节点,u子节点
int i,j,k,v;
for(i=head[u];i;i=e[i].next){
v=e[i].to;
if(v==fa)continue;//遇到父节点,跳过
dfs(v,u);//先搜到底,目标叶节点
sz[u]+=sz[v]+1;//u有分支,故用sz[u]+;+1表示u,v之间的这根树枝
for(j=min(sz[u],q);j;j--)
for(k=min(sz[v],j-1);k>=0;k--){//注意此处条件是k>=0
f[u][j]=max(f[u][j],f[u][j-1-k]+f[v][k]+e[i].w);
}
}
}
int main(){
int n,i,u,v,w;
scanf("%d%d",&n,&q);
for(i=1;i<n;i++){
scanf("%d%d%d",&u,&v,&w);
add(u,v,w),add(v,u,w);//无向图
}
dfs(1,-1);//从根搜起
printf("%d\n",f[1][q]);
return 0;
}
该题收获:
自根向树叶节点遍历,自树叶节点向根节点开始做事。
树的子节点数量求法。
树上使用01背包。
自创数据对01背包进行模拟,更深入的了解了01背包空间上降维的原因。