博客

给定一张无向图，求图中一个至少包含 3 个点的环，环上的节点不重复，并且环上的边的长度之和最小。

该问题称为无向图的最小环问题。

你需要输出最小环的方案，若最小环不唯一，输出任意一个均可。

输入格式

第一行包含两个整数 N 和 M，表示无向图有 N个点，M 条边。

接下来 MM 行，每行包含三个整数 u，v，l，表示点 u 和点 v 之间有一条边，边长为 l。

输出格式

输出占一行，包含最小环的所有节点（按顺序输出），如果不存在则输出

No solution.

。

数据范围

1≤N≤100,

1≤M≤10000,

1≤l<500

输入样例：

5 7
1 4 1
1 3 300
3 1 10
1 2 16
2 3 100
2 5 15
5 3 20

输出样例：

1 3 5 2

Floyd o(n3)

解题思路：

根据floyd算法假设当前正在枚举第k个点（floyd的最外一层循环的变量）根据floyd的性质当前只计算了经过编号为1 ~ k – 1的点而此时因为k点还未被计算因此我们可以假设以k点为固定点计算k点所在的最小环：

如何计算最小环？？？

因为只计算了编号为1 ~ k – 1的点所以我们可以枚举两个点i， j从i -> k -> j即为一个最小环

因为k是固定点所以i -> k, k -> j长度固定分别为g[i][k], g[k][j]

因此环的总长度为g[k][i] + d[i][j] + g[j][k]按照从k -> i -> j的顺序记录

这条路径有两个性质：

1：路径i -> k与路径k -> j不能有交集

证明假设有交集：如图

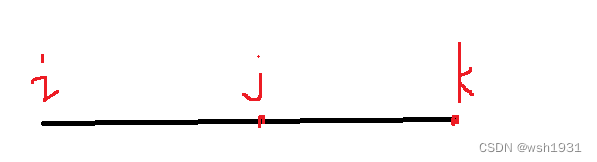
则最小值就不是从i -> k, k -> j

2：在i~j的最短道路中，一定没有环

#include <cstdio>
#include <cstring>
#include <iostream>

using namespace std;

const int N = 110, INF = 0x3f3f3f3f;

int n, m;
int pos[N][N];//记录的是从i -> j中有哪些点
int path[N], cnt;//记录的是最小环中有哪些点
int d[N][N], g[N][N];

void get_path(int i, int j)
{
    if (!pos[i][j]) return ;//说明i -> j没有任何点，即(i, j)是一条边，直接返回
    
    int k = pos[i][j];
    get_path(i, k);//按照环的顺序先记录左半边
    path[cnt ++ ] = k;
    get_path(k, j);
}

int main()
{
    cin >> n >> m;
    
    memset(g, 0x3f, sizeof g);
    for (int i = 1; i <= n; i ++ ) g[i][i] = 0;
    
    while (m -- )
    {
        int a, b, c;
        scanf("%d %d %d", &a, &b, &c);
        g[a][b] = g[b][a] = min(c, g[a][b]);
    }
    
    int res = INF;
    memcpy(d, g, sizeof g);
    for (int k = 1; k <= n; k ++ )
    {
        for (int i = 1; i < k; i ++ )//求以k为固定点至少包含3个点的环
            for (int j = i + 1; j < k; j ++ )//从i + 1开始是因为此图为双向图从i -> j和从j -> i是一样的避免重复
                if ((long long)d[i][j] + g[k][i] + g[j][k] < res)//若答案可以更新
                {
                    cnt = 0;
                    res = d[i][j] + g[k][i] + g[j][k];//记录点的顺序为k -> i -> (i -> j的中间点) -> j
                    //根据floyd算法d[i][j]记录的是从1 ~~ k - 1的最小值
                    path[cnt ++ ] = k;//按照顺序先记录k这个固定点
                    path[cnt ++ ] = i;//记录i点
                    get_path(i, j);//记录i -> j中间点不包括(i, j);
                    path[cnt ++ ] = j;//记录j点
                }
        for (int i = 1; i <= n; i ++ )
            for (int j = 1; j <= n; j ++ )
                if (d[i][j] > d[i][k] + d[k][j])//floyd算法
                {
                    d[i][j] = d[i][k] + d[k][j];
                    pos[i][j] = k;//若可以被更新记录i -> j的中间点
                }
    }
    
    if (res == INF) puts("No solution.");
    else
    {
        for (int i = 0; i < cnt; i ++ ) printf("%d ", path[i]);
        puts("");
    }
    
    return 0;
}