1. 问题描述:
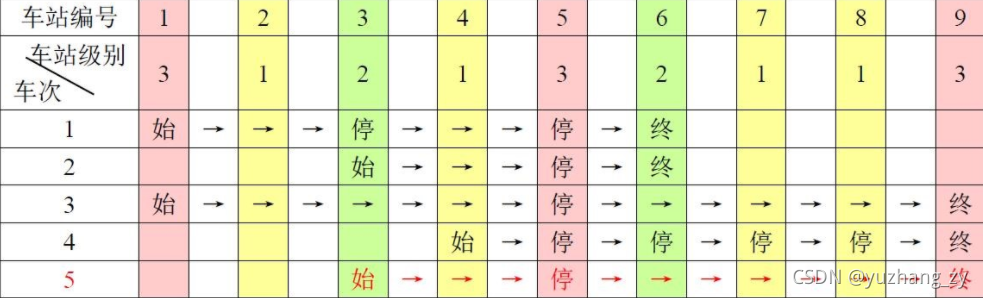
一条单向的铁路线上,依次有编号为 1,2, …, n 的 n 个火车站。每个火车站都有一个级别,最低为 1 级。现有若干趟车次在这条线路上行驶,每一趟都满足如下要求:如果这趟车次停靠了火车站 x,则始发站、终点站之间所有级别大于等于火车站 x 的都必须停靠。(注意:起始站和终点站自然也算作事先已知需要停靠的站点) 例如,下表是 5 趟车次的运行情况。其中,前 4 趟车次均满足要求,而第 5 趟车次由于停靠了 3 号火车站(2 级)却未停靠途经的 6 号火车站(亦为 2 级)而不满足要求。现有 m 趟车次的运行情况(全部满足要求),试推算这 n 个火车站至少分为几个不同的级别。
输入格式
第一行包含 2 个正整数 n,m,用一个空格隔开。第 i+1 行(1 ≤ i ≤ m)中,首先是一个正整数 si(2≤si≤n),表示第 i 趟车次有 si 个停靠站;接下来有 si 个正整数,表示所有停靠站的编号,从小到大排列。每两个数之间用一个空格隔开。输入保证所有的车次都满足要求。
输出格式
输出只有一行,包含一个正整数,即 n 个火车站最少划分的级别数。
数据范围
1 ≤ n,m ≤ 1000
输入样例:
9 3
4 1 3 5 6
3 3 5 6
3 1 5 9
输出样例:
3
来源:
https://www.acwing.com/problem/content/description/458/
2. 思路分析:
首先需要屡清楚题目的意思,题目的主要意思是有若干趟的车次,每趟车次有对应的停车站编号,停靠编号有对应的等级,如果火车在某个停靠站x停靠了,所有从始发站到终点站中停靠站等级大于等于x这个车站的等级的车站都需要停靠,这就意味着从始发站到终点站中没有停靠的车站编号等级都是至少比x小1,这里就存在一个小于的不等式关系,所以我们想到图论中的
差分约束(不等式关系约束的图论问题)
,我们可以将每趟车次中从始发站到终点站中停靠车站的编号与未停靠车站的编号分为两个集合,左边的点集为未停靠的车站,右边的集合为停靠的车站,左边集合中的每一个点向右边集合的每一个点,所有边权都是1:
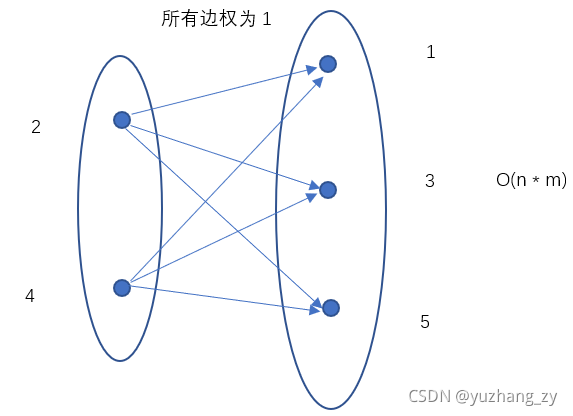
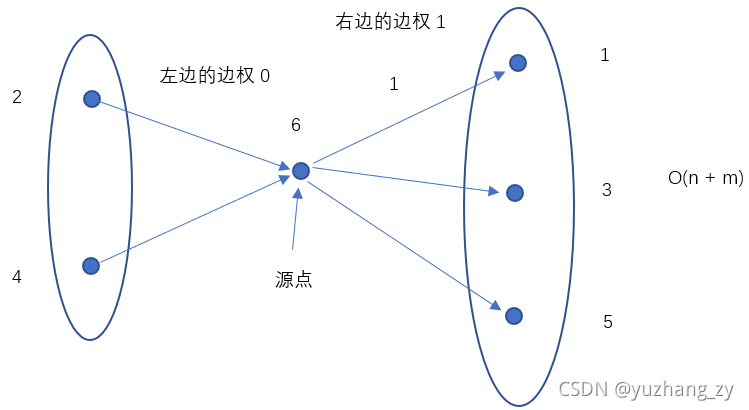
所以我们可以使用一个标记数组st,将所有输入的停靠站的编号标记为1,那么从始发站到终点站中未标记的车站编号就是未停靠的车站,分别对应上图中左边与右边的点的集合,因为左边未停靠的车站的等级都比右边停靠车站的等级至少少1,所以两个集合的边的权重为1,对于每趟车次中分为两个集合进行连边,因为题目中给出的数据都是有解的,所以最终的图是有向无环图,而且因为是差分约束求解最小值的问题,所以我们需要求解单源最长路径,因为每一个车站的等级至少是1,所以我们可以建一个虚拟源点,虚拟源点向其余点连一条长度为1的边,但是在实际写的时候可以发现与将所有点的距离初始化为1的做法是等价的,所以我们只需要将n个点的距离初始化为1即可,具体的做法是:先求解出拓扑排序然后根据拓扑排序的顺序求解单源最长路径,最终求解所有点的最大值那么就是答案。但是这样建图其实是n ^ 2级别的,每一个点都需要向其余点连一条权重为1的边,如果有1000趟车次,每趟车次停靠站的数量为500,所以建边的数量为O(1000 * 500 * 500) = 2.5 * 10 ^ 8,所以肯定会超内存,如果有邻接矩阵来存储其实空间倒是可以但是也需要循环10 ^ 8次,所以也可能会超时,对于这种n ^ 2级别的建图其实有一个比较常用的优化技巧,我们在两个子集建立一个虚拟源点,左边集合的点向源点连一条权重为0的边,虚拟源点向右边集合连一条权重为1的边,可以发现左边节点有右边节点是等价的,从左边的集合中的每一个点可以到达右边集合的每一个点,但是建边的数量其实为O(m),这样建边的时候就从平方级别降到了线性级别。
3. 代码如下:
import collections
from typing import List
class Solution:
# 拓扑排序
def topsort(self, n: int, d: List[int], g: List[List[int]], res: List[int]):
q = collections.deque()
for i in range(1, n + 1):
if d[i] == 0:
q.append(i)
res.append(i)
while q:
p = q.popleft()
for next in g[p]:
d[next[0]] -= 1
if d[next[0]] == 0:
q.append(next[0])
res.append(next[0])
def process(self):
n, m = map(int, input().split())
g = [list() for i in range(n + m + 10)]
d = [0] * (n + m + 10)
for i in range(1, m + 1):
st = [0] * (n + 10)
s = list(map(int, input().split()))
# 始发站与终点站
start, end = s[1], s[-1]
for j in range(1, len(s)):
# 注意是s[j]而不是j, 将所有的停靠站编号标记为1
st[s[j]] = 1
# 建图的优化方式, 建立一个中间节点
ver = n + i
for j in range(start, end + 1):
if st[j] == 0:
g[j].append((ver, 0))
d[ver] += 1
else:
g[ver].append((j, 1))
d[j] += 1
res = list()
# 拓扑排序的节点个数为n + m, 每一趟车次多了一个源点所有拓扑排序总个数为n + m
self.topsort(n + m, d, g, res)
dis = [0] * (n + m + 10)
for i in range(1, n + 1): dis[i] = 1
# 从前往后递推求解最长路径
for i in range(len(res)):
ver = res[i]
for next in g[ver]:
dis[next[0]] = max(dis[next[0]], dis[ver] + next[1])
ans = 0
for i in range(1, n + 1):
# 求解等级的最大值
ans = max(ans, dis[i])
return ans
if __name__ == "__main__":
print(Solution().process())