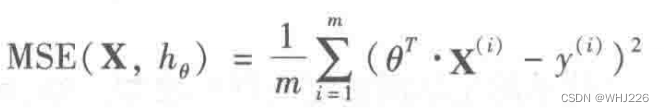机器学习实战（4）——训练模型

训练模型就是设置模型参数直到模型最适应训练集的过程。达到这个目的，我们需要知道怎么衡量

模型对训练数据的拟合程度是好还是差

，最常见的性能指标是

均方根误差（RMSE）

，因此，在训练线性模型时，我们需要找到最小化 RMSE 的
$\theta$
值。在实践中，将均方误差（MSE）最小化比均方根误差（RMSE）更为简单，且二者效果相同。

线性回归模型的MSE成本函数：

$h_{\theta }$
为假设函数，这些符号中与之前我们提到过的唯一区别就是
$h_{\theta }$
，将 h 换成了
$h_{\theta }$
，目的是表明模型被向量参数化（
$\theta$
）。后面，我们为了简化，直接将该函数写成MSE(
$\theta$
) 。

2 标准方程

为了得到使成本函数最小的
$\theta$
值

，有一个闭式求解法—— 一个直接解出结果的数学方程，即标准方程。

标准方程：

举个例子：

常规模块的导入以及图像可视化的设置：

# Common imports
import numpy as np
import os

# to make this notebook's output stable across runs
np.random.seed(42)

# To plot pretty figures
%matplotlib inline
import matplotlib as mpl
import matplotlib.pyplot as plt
mpl.rc('axes', labelsize=14)
mpl.rc('xtick', labelsize=12)
mpl.rc('ytick', labelsize=12)

我们生成一些线性数据：

import numpy as np

X = 2 * np.random.rand(100,1)
y = 4 + 3 * X + np.random.rand(100,1)

数据可视化：

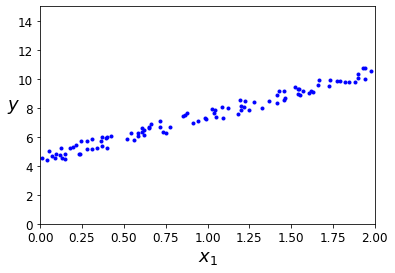
plt.plot(X, y, "b.")
plt.xlabel("$x_1$", fontsize=18)
plt.ylabel("$y$", rotation=0, fontsize=18)
plt.axis([0, 2, 0, 15])
plt.show()

运行结果如下：

现在我们使用标准方程来计算
$\hat{\theta }$
。使用

NumPy的

线性代数模块

（np.linalg）

中的

inv() 函数

对矩阵求逆，并用

dot() 方法计算矩阵的内积

：

X_b = np.c_[np.ones((100,1)), X]
theta_best = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y) #标准方程求解

theta_best

运行结果如下：

array([[4.51359766],
       [2.98323418]])

这里我们讲一下np.c_和np.r_

np.c_[]可以拼接多个

数组

，要求待拼接的多个数组的

行数

必须相同。

np.r_[]可以拼接多个数组，要求待拼接的多个数组的

列数

必须相同

我们实际用来生成数据的函数应是

$y = 4+3x_{0}+$

高斯噪声。因此我们期待的是
$\theta _{0} = 4$
，
$\theta _{1}=3$
，但噪声的存在使其不可能完全还原为原本的函数。

我们用
$\hat{\theta }$
做出预测：

X_new = np.array([[0],[2]])
X_new_b = np.c_[np.ones((2,1)), X_new]

y_predict = X_new_b.dot(theta_best)
y_predict

运行结果如下：

array([[ 4.51359766],
       [10.48006601]])

绘制模型预测结果：

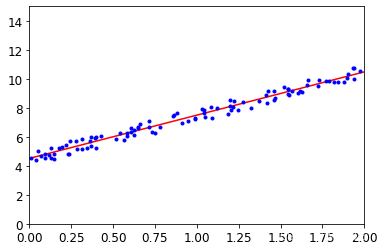
plt.plot(X_new , y_predict, "r-")
plt.plot(X, y, "b.")
plt.axis([0, 2, 0, 15])
plt.show()

运行结果如下：

拓展：Scikit-Learn的等效代码如下：

Scikit-Learn将偏置项（intercept_）和特征权重（coef_）分类开了。
from sklearn.linear_model import LinearRegression
lin_reg = LinearRegression()
lin_reg.fit(X, y)
lin_reg.intercept_, lin_reg.coef_
运行结果如下：
(array([4.51359766]), array([[2.98323418]]))
lin_reg.predict(X_new)
运行结果如下：
array([[ 4.51359766],
       [10.48006601]])

3 复杂度

标准方程求逆的矩阵
$X^{T}\cdot X$
，是一个n×n矩阵（n是特征数量）。对这种矩阵求逆的计算复杂度通常为
$O\left ( n^{2.4} \right )$
到
$O\left ( n^{3} \right )$
之间。如果特征数量翻倍，那么计算时间将乘以大约
$2^{2.4} = 5.3$
倍到
$2^{3} = 8$
倍之间。

幸运的是，相对于训练集中的实例数量来说，方程是线性的，所以能够有效的处理大量的训练集，只要内存足够。同样，线性回归模型一经训练（不论是标准方程还是其他算法），预测就非常快速。

4 梯度下降

梯度下降是一种非常通用的优化算法，能够为大范围的问题找到最优解。梯度下降的中心思想就是迭代地调整参数从而使成本函数最小化。梯度下降的做法：通过测量参数向量
$\theta$
相关的误差函数的局部梯度，并不断沿着降低梯度的方向调整，直到梯度降为0，到达最小值。具体来说，首先使用一个随机的
$\theta$
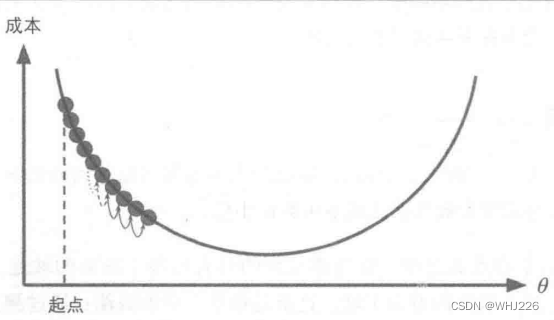
值（随机初始化），然后逐步改进，每次踏出一步，每一步都尝试降低一点成本函数，直到算法收敛出一个最小值，如下图。

梯度下降中一个重要参数是每一步的步长，这取决于超参数的学习率。如果学习率太低，算法需要经过大量的迭代才能收敛。如果学习率太高，导致算法发散，值越来越大，最后无法找到最好的解决方案。

梯度下降的挑战：

如果随机初始化，算法从左侧起步，那么会收敛到一个局部最小值，而不是全局最小值；如果算法从右侧起步，那么需要经过很长时间才能越过山谷，如果停下得太早，可能永远达不到全局最小值。

幸运的是，

线性回归模型的MSE成本函数恰好是个凸函数

，这意味着连接曲线上任意两个点的线段永远不会跟曲线相交，也就是说不存在局部最小，只有一个全局最优值。同时，它是一个连续函数，所以斜率不会产生陡峭的变化。结论就是：即便乱走，梯度下降都可以趋近到全局最小值。

下图所示的梯度下降很好地体现了不同特征尺寸差别，左边的训练集上特征1和特征2具有相同的数值规模，而右边的训练集上，特征1的值比特征2要小得多。（因为特征1的值比较小，所以
$\theta _{1}$
需要更大的变化来影响成本函数，这就是为什么碗形会沿着
$\theta _{1}$
轴拉长）。我们在应用梯度下降时，通过归一化和标准化处理可以保证所有特征值的大小比例都差不多。

5 批量梯度下降

要实现梯度下降，我们需要计算每个模型关于参数
$\theta _{j}$
的成本函数的梯度。

换言之，我们需要计算的是如果改变
$\theta _{j}$
，成本函数会改变多少，这也被称为偏导数。

关于参数
$\theta _{j}$
的成本函数的偏导数，记作
$\frac{\partial }{\partial \theta _{j}}MSE\left ( \theta \right )$
。

原文链接：https://blog.csdn.net/WHJ226/article/details/126359401

1 线性回归

2 标准方程

3 复杂度

4 梯度下降

5 批量梯度下降

你可能也喜欢