傅里叶参考视频 :1Blue3Brown——https://www.bilibili.com/video/BV1pW411J7s8?spm_id_from=333.999.0.0&vd_source=987ca75cfd3c2a6c6aef5f869b334d44
拉普拉斯参考视频:
https://www.bilibili.com/video/BV1Hs411p7XY?spm_id_from=333.337.search-card.all.click&vd_source=987ca75cfd3c2a6c6aef5f869b334d44
傅里叶
傅里叶变换公式如下:
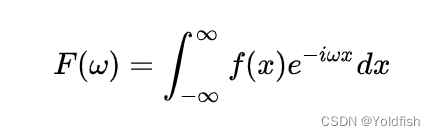
公式每部分含义:
f(x)是原函数,不用做过多说明;
e^-i表示在复平面上的一个单位圆;
wx在x处这个单位圆的旋转角度;
f(x)*e^-iwx表示f(x)在这个单位圆上的位置,当f(x)=0时在圆心,f(x)=1时在圆上;
积分符号意味着f(x)在这个单位圆上所有点的相加,这意味着如果我们把积分后的值除以采样时间,就相当于求这个图形的形心,也就得到了幅值。
拉普拉斯
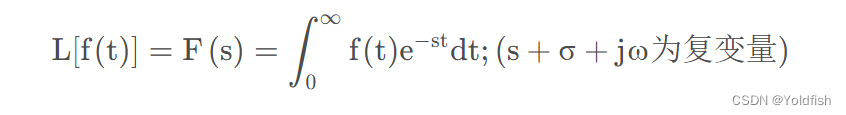
从公式可以看出,与福利相比就多了个实数域。
将exp(a+iw)拆分成exp(-a)*exp(-iw),然后把f(t)*exp(a)联合起来看,就相当于求f(t)*exp(-a)的傅里叶变换。
那么当a=0时,就等同于求f(t)的傅里叶变换。
再来看,如果f(t)包含exp相关的分量例如f(t) = exp(t),那么就有f(t)*exp(-a),这个啥时候如果a=1就刚好抵消了;
这个思路与上述傅里叶相同,可以看出,a类似于w可以提取出原函数中的exp的分量。
带着这个思路,我们可以直接推测出常见函数的拉普拉斯变换。
如下:

由于当我们对周期型号做傅里叶变换时,在对应频率上能够得到一条高高的竖线。
对应到拉普拉斯变换中也一样,令拉普拉斯变换后的值等于无穷大的时候,也就是分母等于0时,就近似可以看长傅里叶变换得到的那个竖线。
而那个竖线对应的坐标就是原信号的周期频率,例如看上方sin(wt)的拉普拉斯变换,s=wi时,分母为零,且w=0时值为0,就可以推测出,原函数的周期为w。
同理,exp(-at), 变换后的分母,当s=-a时,为0,这时只有实数解,那么说明原函数没有周期分量,只有exp分量,其分量的值为-a。