博客

目录

A    AcWing 4867. 整除数

1.题目描述

2.思路分析

3.代码实现

B    AcWing 4868. 数字替换

1.题目描述

2.思路分析

3.代码实现

A    AcWing 4867. 整除数

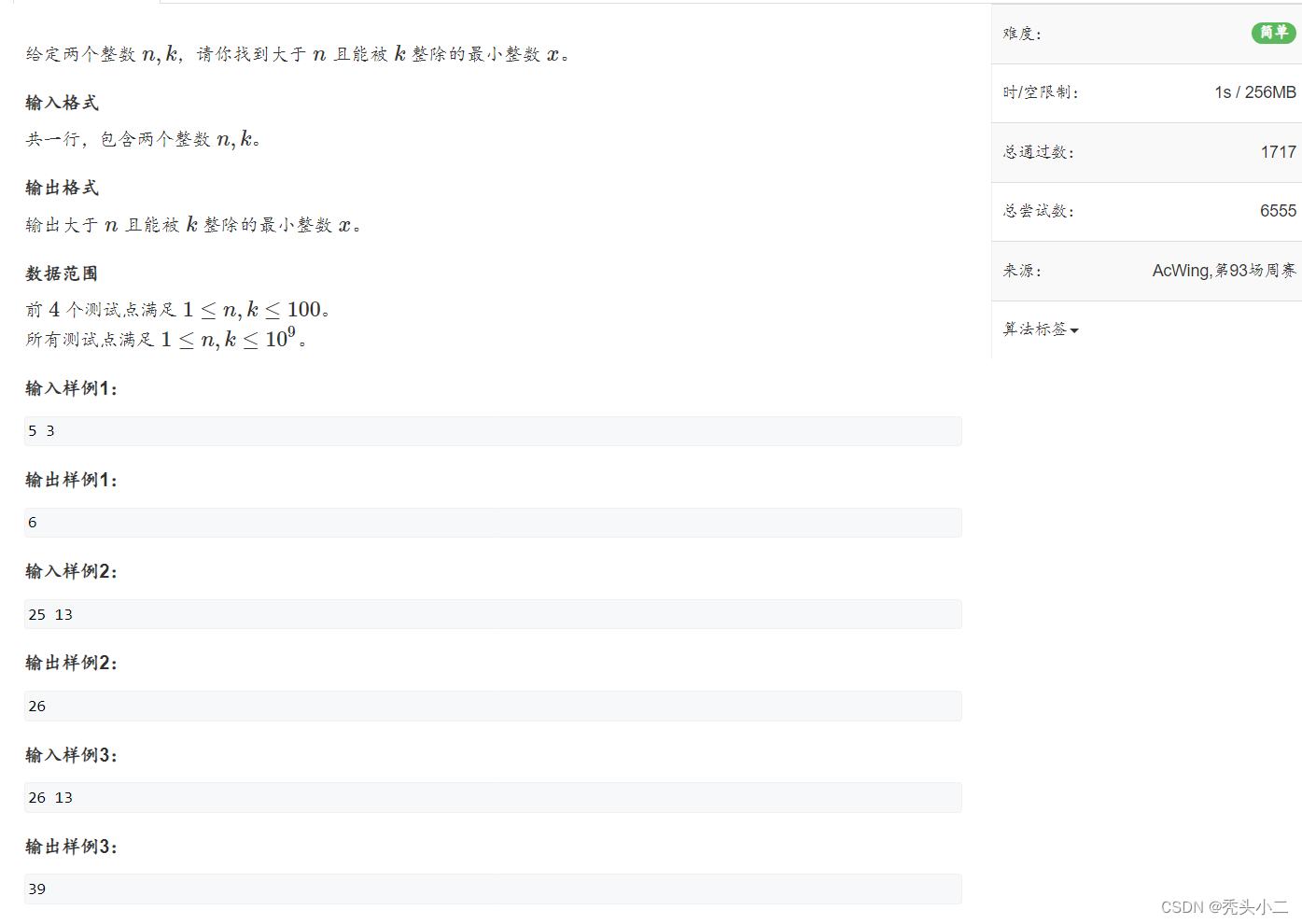
1.题目描述

2.思路分析

• 为什么不能直接暴力？
  

数据：1 ≤ n, k ≤ 10 ** 9

1s内最多运行到10 ** 8次方左右，所以不能直接暴力

• 那怎么做呢？
  

需要一定

数学思维

：

易知：被除数 ÷ 除数 = 商 ······ 余数

故：被除数 = 除数 * 商 + 余数

即：n = k*q+r

当r = 0时，ans = k*(q+1)

当r != 0时，ans = k*(q+1)

3.代码实现

n, k = map(int, input().split())
print(k * (n // k + 1))

B    AcWing 4868. 数字替换

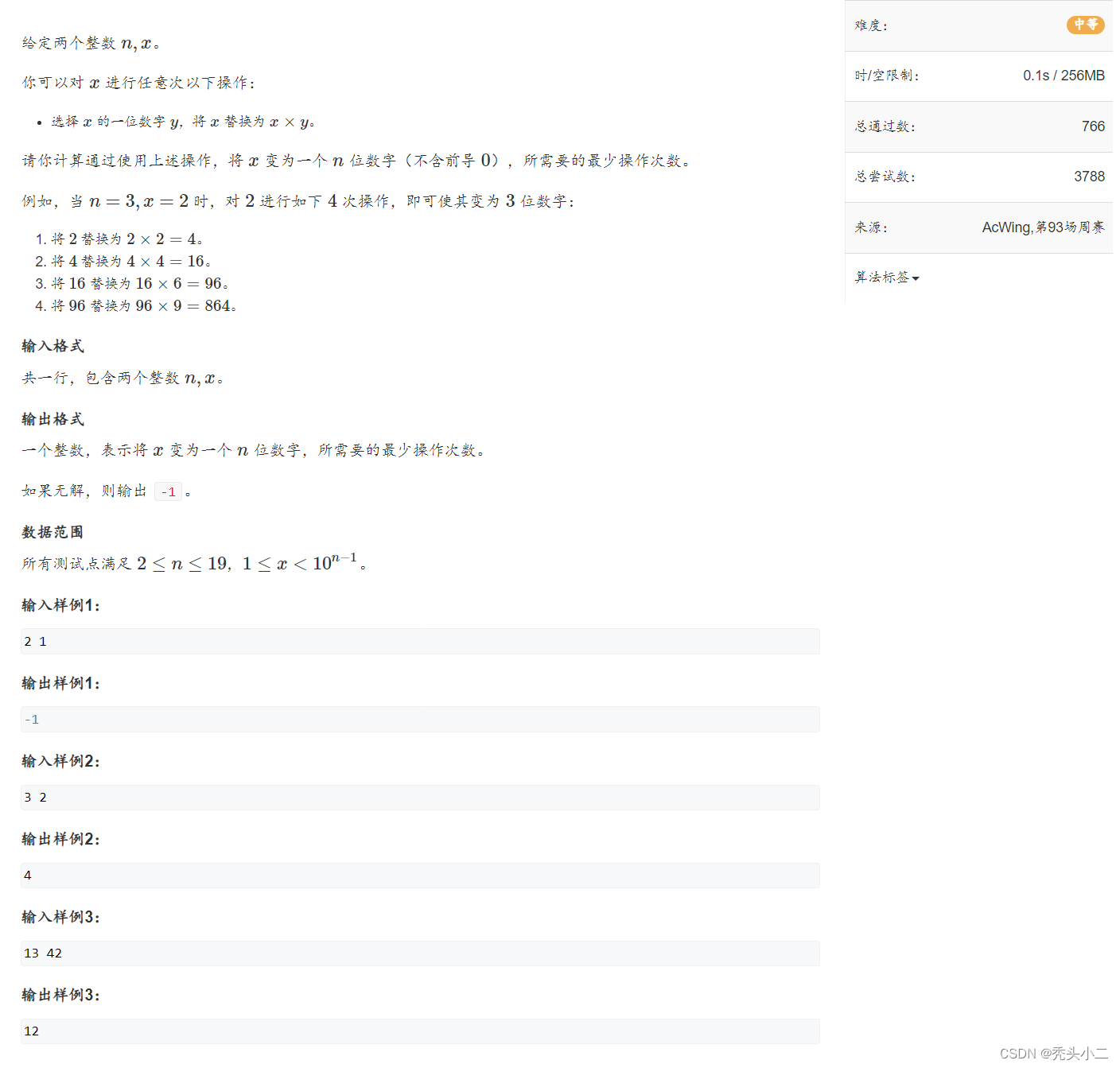
1.题目描述

2.思路分析

没想太多，

其实是dfs+剪枝什么的也不会

直接bfs枚举出所有每次两数相乘的结果然后统计边数，

如果x变为n位数字返回边数，

否则返回-1

3.代码实现

n, x = map(int, input().split())


def bfs(s):
    q = [s]
    seen = {s}
    cnt = 0
    while q:
        for _ in range(len(q)):
            v = q.pop(0)
            if len(str(v)) == n:
                return cnt
            for w in set([int(i) * v for i in str(v)]):
                if w not in seen:
                    q.append(w)
                    seen.add(w)
        cnt += 1
    return -1


print(bfs(x))

如有帮助可以点赞收藏嘛~

如有不足或不解之处欢迎评论留言~