互为对偶的两个线性规划问题的解存在关系是?
提示:
题目
互为对偶的两个线性规划问题的解存在关系
A原问题无可行解,对偶问题也无可行解
B对偶问题有可行解,原问题可能无可行解
C若最优解存在,则最优解相同
D一个问题无可行解,则另一个问题具有无界解
二、解题
链接:
https://www.nowcoder.com/questionTerminal/076987f0256c462097a2c0bc3c639197
来源:牛客网
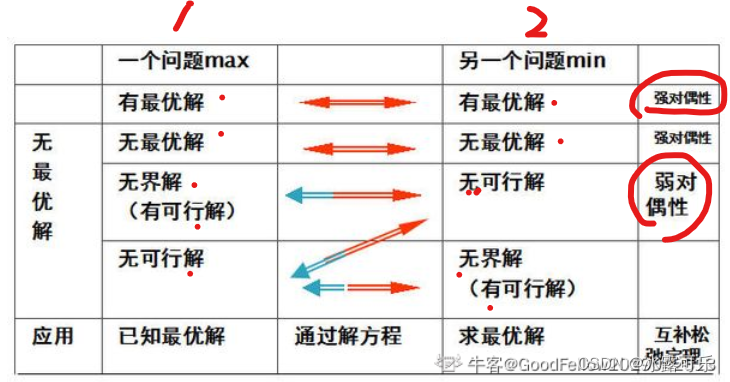
任何一个线性规划都存在对偶问题,对偶问题的对偶问题就是原问题。
互为对偶的线性规划,
一个无最优解,另一个也无最优解
,
但是一个
无可行解,另一个可能有可行解
,因此A错误,B正确。
若
最优解存在,其应该是对偶的
,即,并非相同,因此C错误。
D选项
一个问题无可行解,另一个问题可能也无可行解
,
可能具有无界解
,因此错误。
在线性规划早期发展中最重要的发现就是
对偶问题
,
即每一个线性规划问题(称为原始问题)都有一个与它对应的对偶线性规划问题(称为对偶问题)
总结
提示:重要经验:
3)笔试求AC,可以不考虑空间复杂度,但是面试既要考虑时间复杂度最优,也要考虑空间复杂度最优。