一、状态轨迹的线性化方法
1.理解:
第四章的期望轨迹给出了路径上每个点的状态信息(包括状态量和控制量),这类轨迹比较规则,比如直线、圆等,因此其控制量也容易得到,而对于“期望轨迹无法给出所有状态点的信息”的情况,则需要采用下面的算法。
2.算法详细推导
第五章采用的算法是通过对系统输入持续不变的控制量得到状态轨迹。
目录
①前言
以及:龚建伟等.《无人驾驶车辆模型预测控制》(第2版)
同时对自己在代码实现时需要用到的推导细节给出了更加详细的说明,以帮助自己更好的理解~算是自己学习过程的记录。好了,下面就正式开始吧!
模型预测控制的核心是通过建立基于状态量的误差量的状态空间方程来推导。第四章通过车辆的运动学方程,采用了非线性系统线性化方法中的第一种:存在参考系统的线性化方法。
②车辆的运动学方程
车辆的运动学方程推导过程略,结果如下:

即:
·····························(
1.2
)
选取系统的状态量为
,控制量
主要思想:假设参考轨迹给定,且参考轨迹在任意时刻其状态量和控制量均满足:
·····························(
1.3
)
其中,
,
。
ps①: 1.
是状态转移函数,就理解为数学中表示函数的符号就可以了;
2.
为车辆后轴中心坐标,
为车辆的航向角,
为前轮偏角,
为车辆后轴中心 的速度;
3.在该车辆模型中,状态量个数是3个,用
表示;控制量个数是2个,用
表示,在之后的推导过程的说明中,就直接用
来表示~~~
③线性化过程
上面的运动学方程
是非线性的,所以需要对其进行线性化。对
在参考轨迹点采用泰勒级数展开并忽略高阶项,只保留一阶项:

将(1.4)式减去(1.3)式,得:

记:
,
,
。
ps②:
、
、
矩阵的大小均为:
,
、
、
矩阵的大小均为:
。
因此上式可以写成:
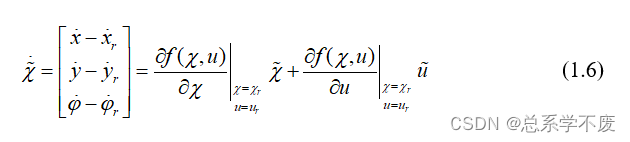
其中:
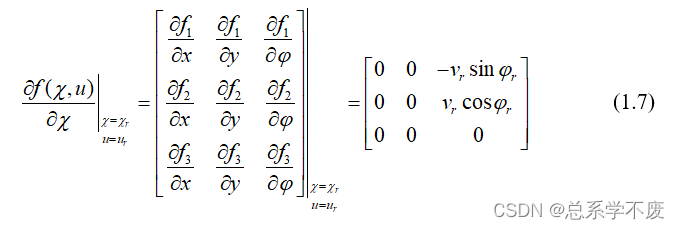
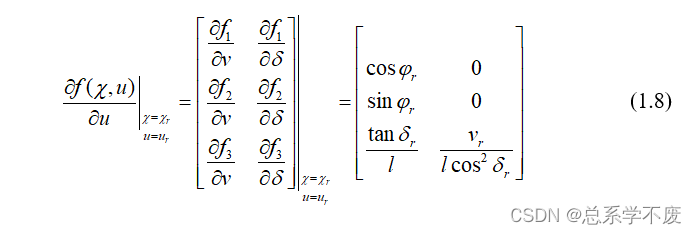
ps③:此运动学模型因为较为简单,故其雅克比矩阵手算其实更为方便,但当遇到比较复杂 的动力学模型时,需借助matlab进行求解,具体可见《无人驾驶车辆模型预测控制》
第五章—> 。
因而线性化后的模型可以写成:
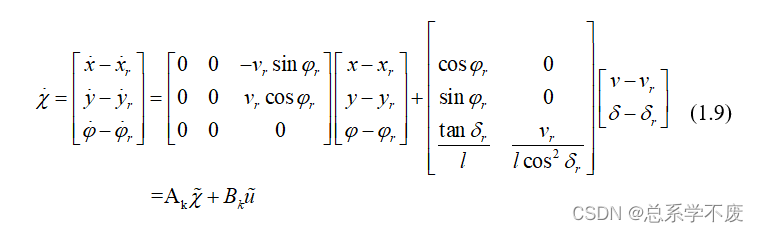
④离散化
对上式采用向前欧拉法进行离散化:
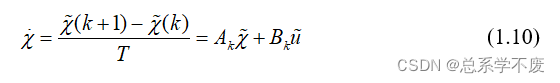
其中,
为系统采样时间。
然后得:
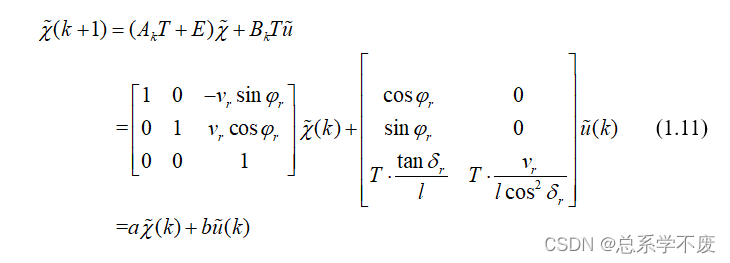
ps④:
矩阵的大小:
;
矩阵的大小:
。
接下来构造一个新的状态量(
把原来的
状态量偏差
和
控制量偏差
整合到一起
):
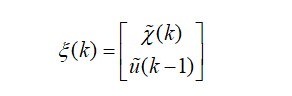
ps⑤:新构造的状态量
矩阵的大小为:
;
分别是状态量个数和控制量个 数。
⑤推导下一时刻状态
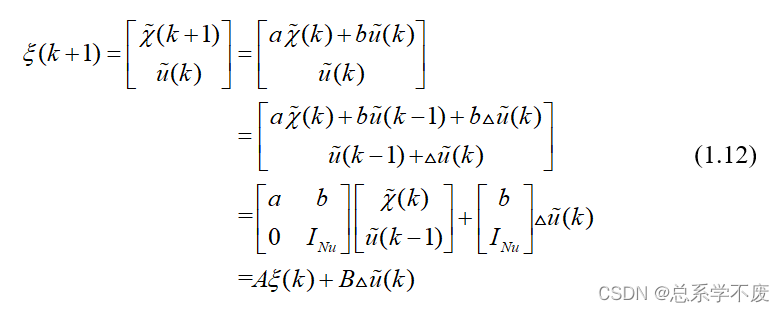
ps⑥: 1.上面
矩阵中的
矩阵的大小为:
;
2.
矩阵的大小为:
,在第四章中即为
;
3.
矩阵的大小为:
,在第四章中即为
;
4.
矩阵的大小为:
。
输出为:
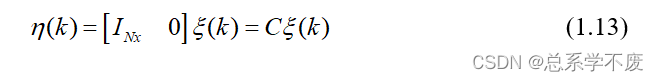
ps⑦: 1. 上面的
矩阵的大小并不一定是
,这要看输出状态量的个数,我们将 输出量的个数定义为
。注意:此处的输出量的个数有别于代码中的初始化子函数 中的输出量个 数!
指的是“状态量”中的输出个数,也就是说
。而在第四章中
。
2. 所以上面
矩阵中的
矩阵的大小为:
,写成
;那么
矩阵的大小为:
;写成
;
矩阵的大小为:
,写成
。为了方便书写我们在之后的部分直接用
代替
。如果想详细知道后面部分各个矩阵的具体大小,可参考我第五章的学习内容:————————————
⑥迭代推导
控制时域
,预测时域
,且
。
新的状态量:
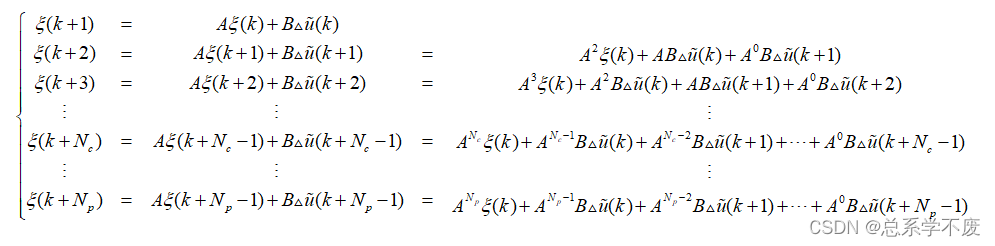
输出:
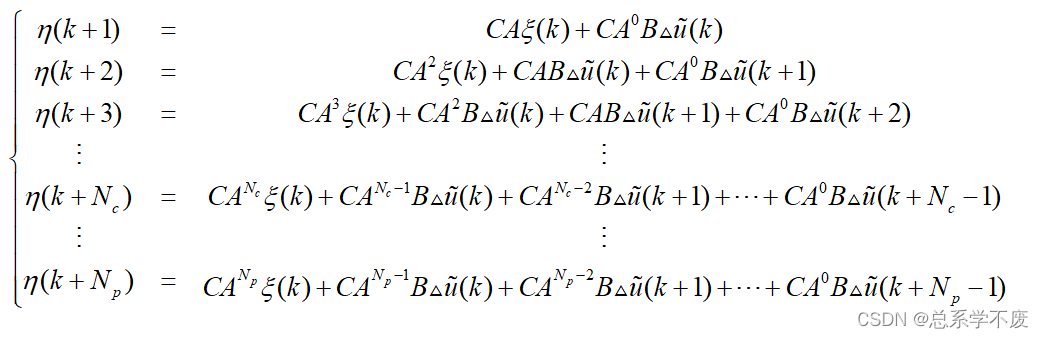
ps⑧:因为
矩阵的大小为:
,
矩阵的大小为:
,
矩阵的大小为:
。所以
矩阵的大小为:
,
矩阵 的大小为:
,
矩阵的大小为:
。
总结规律可得输出方程为:

其中,
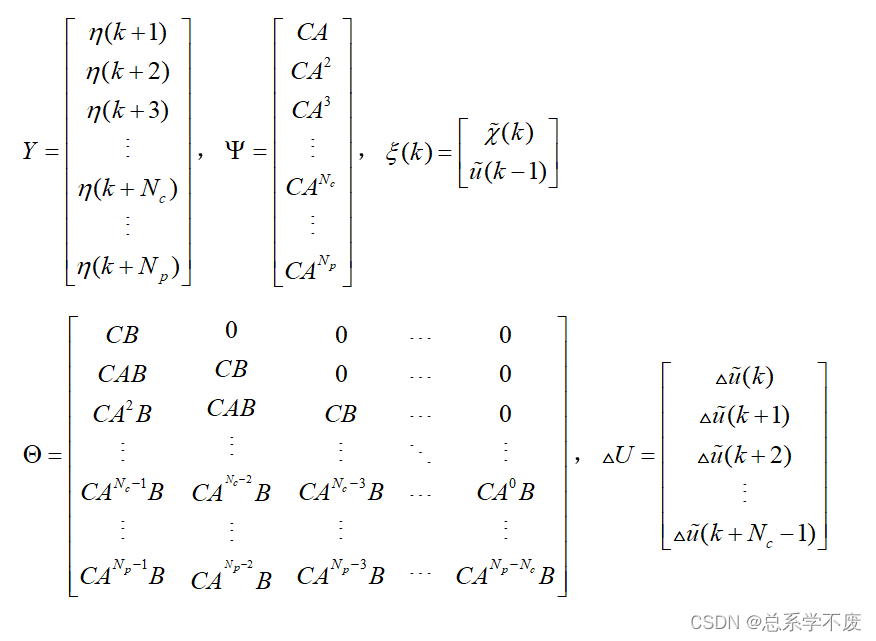
ps⑨:1.以下带”
“结尾的矩阵指的是代码中的元胞;
2.
矩阵大小为:
,
矩阵大小为:
,
矩阵 的大小为
,
矩阵的大小为:
。
矩阵大小为:
,又因
矩阵的大小为:
,所以
矩阵的大小为:
,且其中每个
矩阵的大小为:
,(同
一样),
矩阵的大小为:
,
矩阵的大小为:
。
⑦目标函数优化
选择目标函数为:
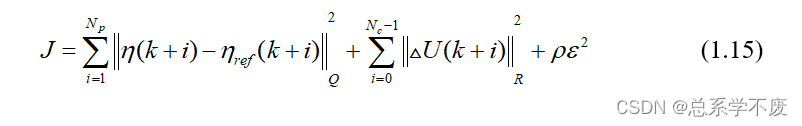
并定义系统输出量的参考值为:
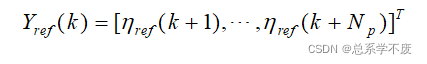
令
,将式(1.14)代入目标函数式(1.15)中,有:
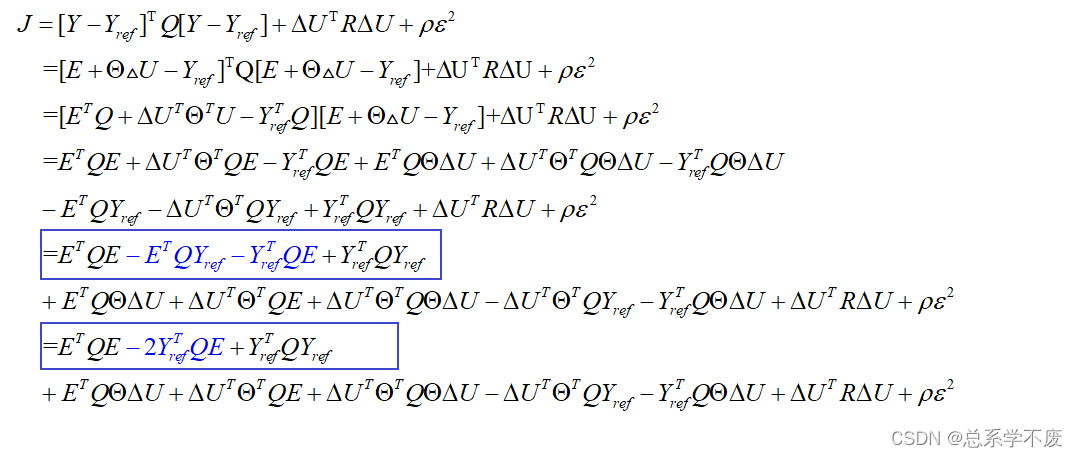
上面方框中的部分与
无关,属于常量,可不加入优化。
ps⑩: 上方蓝色方框中的蓝色字体部分的之所以可以这么合并,是因为,
矩阵和
矩阵是同型矩阵,
和
都是常数,(根据前面推导的
、
、
矩阵的大小即可推导)因而可以合并。
故目标函数简化为:
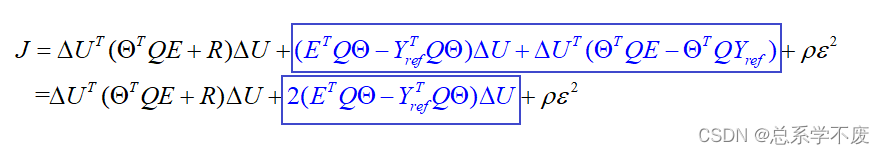
ps⑪:同理,上面第一个方框中的两项也是常数,故可以合并!
故性能评价函数为:
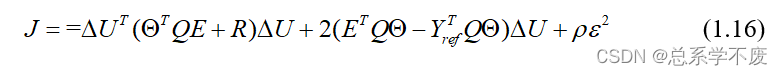
ps⑫: 1.以上的推导过程中,因为:
矩阵的大小为:
,
矩阵的大小为
;
矩阵的大小为:
,
矩阵的大小为:
。所以
元胞的大小为:
,
矩阵大小为:
;
元胞的大小为:
,
矩阵的大小为
。
2.Matlab中二次规划quadprog的标准形式为:
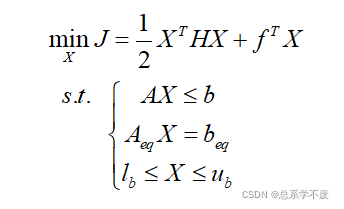
将性能评价函数式(1.16)进行配凑得到:
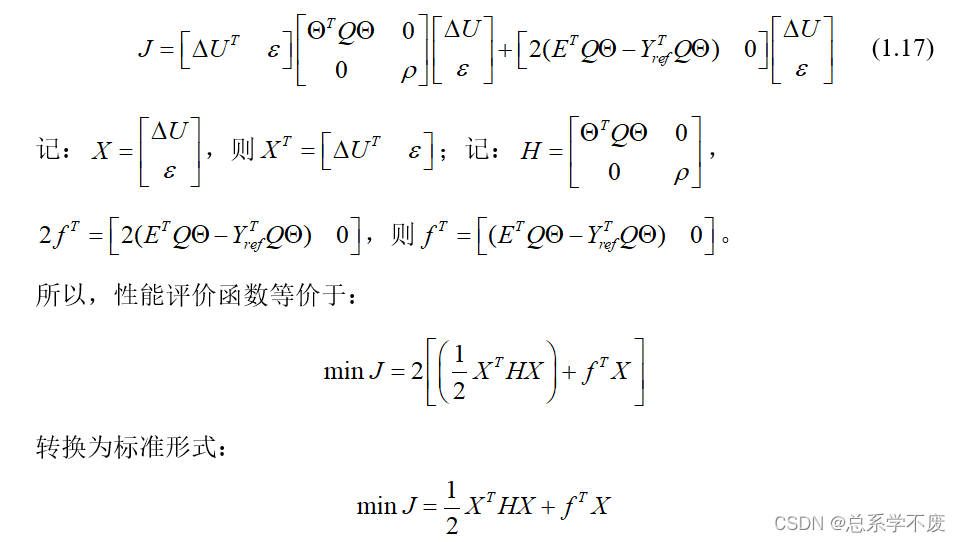
ps⑬: 1.因为
矩阵大小为:
,
矩阵的大小为:
,
元胞的大小为:
,
矩阵大小为:
。所以
矩阵的大小为:
。
矩阵中右上角的
矩阵大小为:
,左下角的
矩阵的大小为:
。
⑧约束条件

ps⑭: 1.
元胞的大小为:
,
矩阵的大小为:
;
元胞的大小为:
,
矩阵的大小为:
;
元胞的大小为:
,
矩阵的大小为:
。
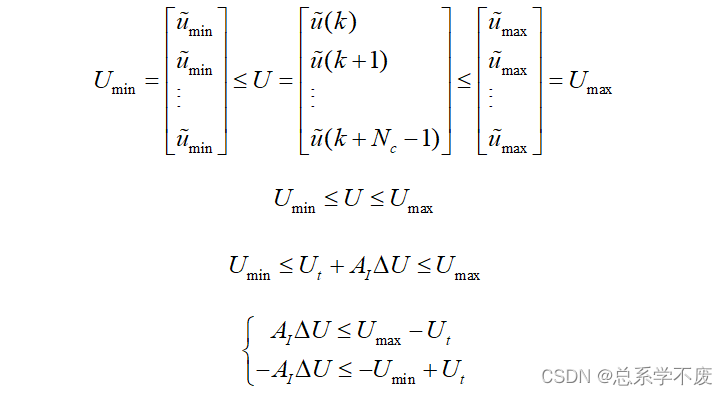
ps⑮:1.
元胞的大小为:
,
矩阵的大小为:
;
同!
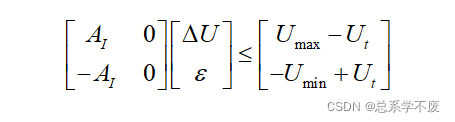
ps⑯:上面两个
元胞的大小为:
,
矩阵的大小为:
。
⑨上下限约束
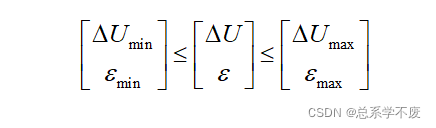
ps⑰:
同
~~~