博客

Github已添加含增量学习的代码，主要还是根据之前参考的代码修改，处理MNIST的结果也已经放在最后一节。已经很久不看这方面的内容。欢迎给原作者代码star（链接在4.1）。

我也是最近才知道除了深度学习，还有一个神经网络叫宽度学习（下文统称BLS）。

1：Introduction

宽度学习是澳门大学科技学院院长陈俊龙和其学生于2018年1月发表的

文章

提出的，文章名为《Broad Learning System: An Effective and Efficient Incremental Learning System Without the Need for Deep Architecture》

据论文所述：深度学习由于计算量太大，计算成本太高，所以提出了一种新的网络结构来解决这个问题。

接下来，我会尽量用最简单的语言来详细介绍这个网络：


你需要提前知道的：BLS的网络结构不是固定的，而是随着学习不断改变的。不要用之前普通深度学习的思路来理解它。

1.1：级联相关网络（本节来自周志华《机器学习》）

上图中红色部分为级联相关网络的一个基本结构，级联相关网络使深度学习的一种方法，所以，他还是再不断地往深了走，以求找到最佳的深度网络。

再看宽度学习的基本结构：



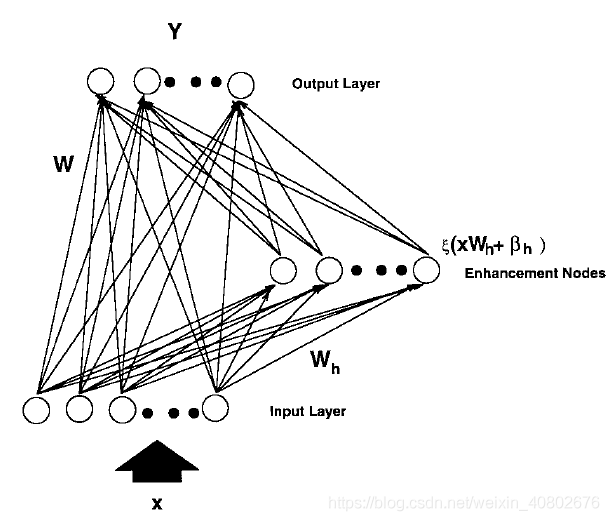
这是随机向量函数连接网络（RVFLNN）的结构，也是宽度学习的基础。你可以看到他与级联相关网络的相似之处。一个是往深了走，一个是往宽了走（当然，RVFLNN不是自动横向添加神经元，后面的宽度学习系统才是不断横向添加神经元）

1.2：随机向量函数连接网络(RVFLNN)

现在，我们来介绍一下RVFLNN，这是宽度学习的基础。

BLS是来源于一个叫

随机向量函数连接网络

random vector functional-link neural network (

RVFLNN

)的网络结构。文章给出了图片：



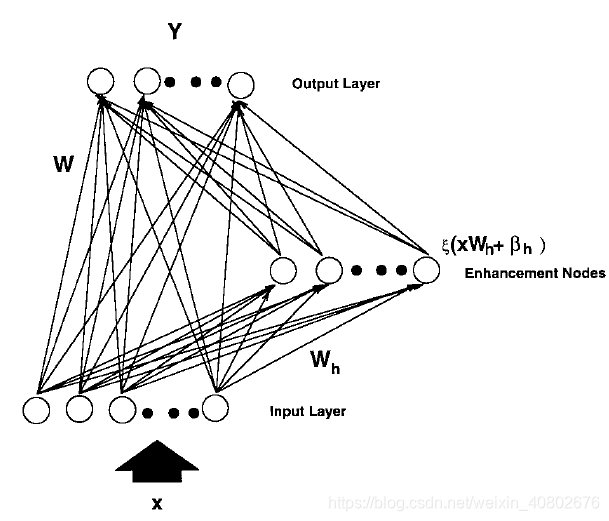
它是这样的：

给定输入X，普通的网络会把X乘上权重，加上偏差之后传入到下一个隐藏层，但是，RVFLNN不只这样，它乘上一组随机的权重，加上随机的偏差之后传入到一个叫增强层（enhance layer），

注意

，这组权重在以后

不会变了

。传入增强层的数据经激活函数（也只有增强层有激活函数）得到H。

之后，把原本的输入X和增强层的计算结果H合并成一个矩阵（这两个矩阵都是*x1的类型），称为A，A=[X|H]，把A作为输入，乘上权重，加上偏差之后传到输出层。

把上面的图片中增强层挪到输入层就成这样了。



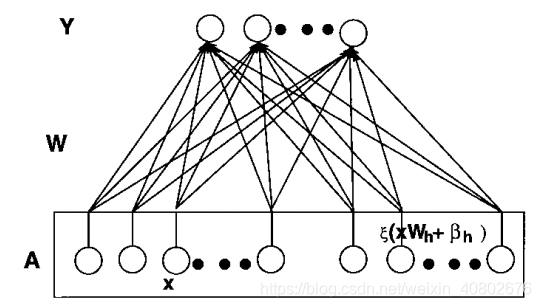
第二次计算的权重和偏差才是我们需要计算的结果。那么怎么计算呢？？

我们想要让


AW = Y

A是已知的，Y也是已知的。所以W=A

^-1

Y不就计算出来了吗。

但是矩阵A是一个*x1的矩阵，是没有逆矩阵的，但是，没有逆矩阵，还有伪逆。这下，想要的都有了。

假设训练集为500个样本，label有3种类型。按照普通的神经网络，我们会一个一个将样本传入神经网络，用梯度下降来更新权重。但是对于RVFLNN来说，我们一次性将所有样本传入网络。没有权重更新过程，而是一步直接计算出权重。

下面来举个例子

假设训练集有500个样本，属性有4个，label有3种。那么我们的输入X就是500×4的矩阵。我们设定需要的增强节点为300个，那么输入就是500×304，而我们想要的权重则是304×3的矩阵。如此，输入矩阵与输出矩阵相乘，得到的就是500×3的矩阵。按照上面的理论，我们只需要计算一次伪逆就行了。

2：宽度学习系统（Broad Learning System）

BLS在RVFLNN的基础上再一次改进，尤其是增加了

增量学习

的过程。增量学习就是前文提过的自动横向增加增强节点或者mapping nodes的过程。

2.1：不含增量学习的BLS

不含增量学习的BLS与RVFLNN极为相似。

此时的BLS不再将原始数据直接输入到网络中，而是先经过一番处理，得到mapping nodes。之后，mapping nodes的输入数据就是之前RVFLNN的输入数据。

mapping nodes不是只有一组。它可以有很多组，每一组叫一个mapping feature。同样，enhancement nodes也不是只有一组，也可以有很多组。

如图：



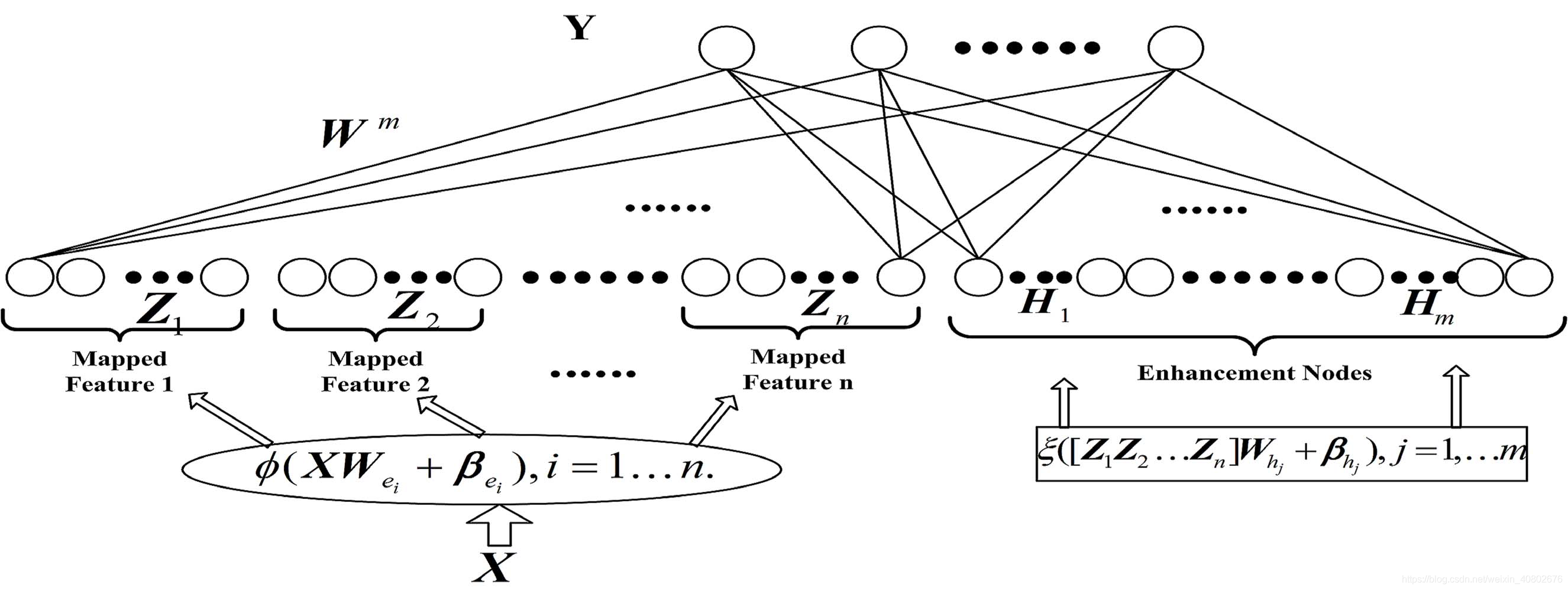
这样的网络结构是你提前设定的，有几组mapping nodes，几组enhancement nodes都是你规定好了的。


再举个例子：

假设训练集有500个样本，属性有4个，label有3种。我们想要10组mapping feature，10组enhancement nodes。每组我们都想要100个节点。

这样mapping nodes就有1000个，enhancement nodes也有1000个。那么我们原始的输入X仍然是500×4的矩阵。但是，我们要先把它变成10个500×100的矩阵。所以我们需要10个4×100的权重矩阵，这个权重我们是随机设定的。

当我们得到10组500×100的mapping nodes的输入Z之后，我们还要得到enhancement nodes的输入H。为此，还需要10组100×100的另一个随机权重（这个权重一般还设置成正交的，可能是为了防止enhancement nodes输入彼此之间的相关性）。之后，我们的输入就是A=[Z|H]，shape为500×2000。这两个随即权重都不再改变。输入到输出权重W的shape为2000×3，同样由求伪逆即可得到。

2.2：增量学习

但是有时我们设定的网络对训练集不能很好的拟合，所以我们就需要增量学习。不断地增加节点，来得到更好的网络结构。



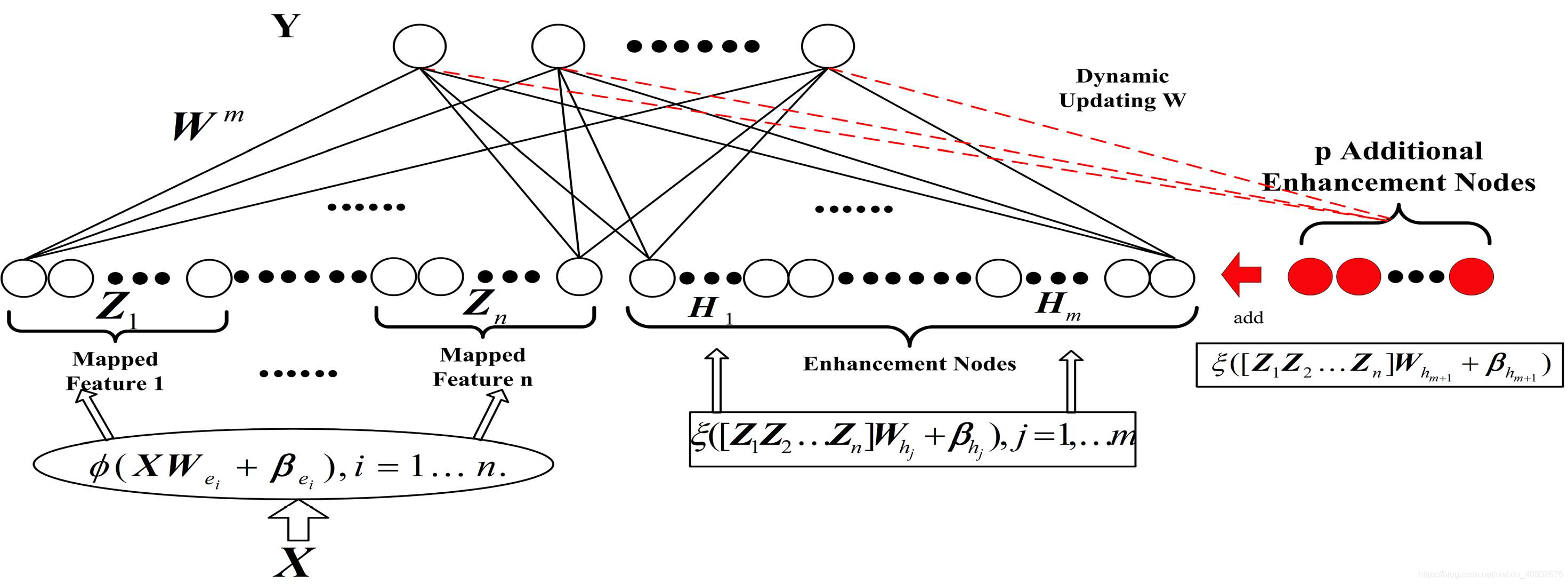
当我们按照不含增量学习的网络训练结束之后，发现效果不够理想，我们就增加其中一种或者两种节点。这样节点增加了，权重也增加了，模型变得更加复杂，效果就可能更好。

增加节点之后，我们需要更新权重。但是，如果要重新求逆就得不偿失了，因为新的A矩阵只是在原矩阵上追加了一部分，大部分还是没变的。所以，作者使用广义的逆矩阵。用下面的公式来更新权重：



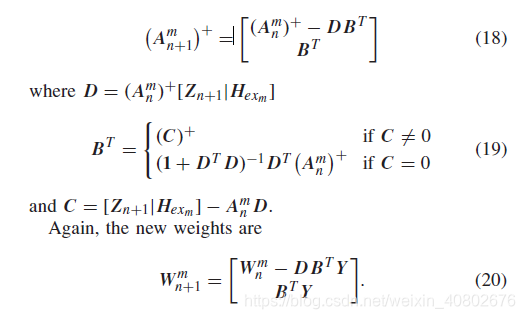
这样的话，每次计算就可以在上一次权重的基础上进行了。

因为我们增加节点可以增加mapping nodes，也可以增加enhancement nodes，所以有两种方法。法：





两种方法都使用了一个

while

循环，当误差一直不满足设定值时，就会一直增加节点。

3：感想

在实际应用中，我们的样本可能有上百万个，特征也可能成千上万，这时，计算一个矩阵的逆简直是不可能的。

但是，bls论文中提出一种办法来解决。当我们第一次计算不含增量的伪逆时，使用的是岭回归，这样就避免了直接计算一个巨大的矩阵的伪逆。之后，我们更新权重只使用广义逆计算。和最初的伪逆计算的计算量相比，要少得多。

4：实验

4.1：Github

bls实现代码：

我的

github


，


主要参考的（有含增量学习的代码）



github

我在他的基础上删除了一些冗余的部分，添加了更多的注释。

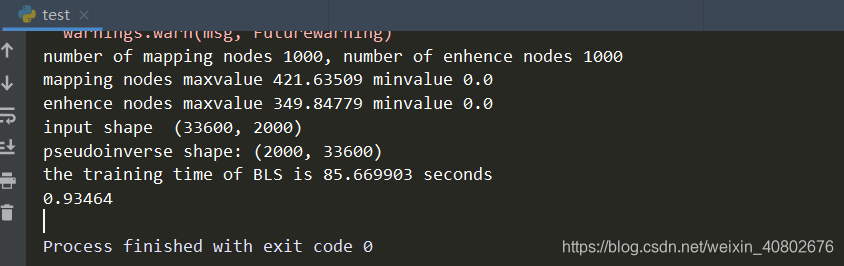
4.2： 不含增量学习的MNIST结果：

测试集上准确率0.93464（未调参）

用bls做MNIST的程序我已经放在

Github


上了。

4.3：直接求训练集X的伪逆，进而求得W🎂

在不含增量学习的bls中，通过对训练集的X乘上一系列随机的权重，得到的结果再乘上一系列随机的权重。最后组合在一块，求其伪逆，和y相乘得到权重W。那么，如果我们不乘那么多随机权重呢。而是直接用原始数据集X求伪逆，再求W呢？

import numpy as np
import pandas as pd
from sklearn import preprocessing  # 用来转化为独热编码
from sklearn.model_selection import train_test_split

class scaler:
    def __init__(self):
        self._mean = 0
        self._std = 0

    def fit_transform(self,traindata):
        self._mean = traindata.mean(axis = 0)
        self._std = traindata.std(axis = 0)
        return (traindata-self._mean)/(self._std+0.001)

    def transform(self,testdata):
        return (testdata-self._mean)/(self._std+0.001)


class net(object):
    def __init__(self):
        self.W = None
        self.normalscaler = scaler()
        self.onehotencoder = preprocessing.OneHotEncoder(sparse = False)

    def decode(self,Y_onehot):
        Y = []
        for i in range(Y_onehot.shape[0]):
            lis = np.ravel(Y_onehot[i,:]).tolist()
            Y.append(lis.index(max(lis)))
        return np.array(Y)

    def fit(self, X, y):
        X = self.normalscaler.fit_transform(X)
        y = self.onehotencoder.fit_transform(np.mat(y).T)
        self.W = np.linalg.pinv(X).dot(y)   # 784*10
        print('shape of W is:{}'.format(self.W.shape))

    def predict(self, X_test):
        X_test = self.normalscaler.transform(X_test)
        y = X_test.dot(self.W)
        print('predictions of y shape:{}'.format(y.shape))
        return self.decode(y)
if __name__ == '__main__':

    # load the data
    train_data = pd.read_csv('./train.csv')
    test_data = pd.read_csv('./test.csv')
    samples_data = pd.read_csv('./sample_submission.csv')

    label = train_data['label'].values
    data = train_data.drop('label', axis=1)
    data = data.values
    print(data.shape, max(label) + 1)

    traindata,valdata,trainlabel,vallabel = train_test_split(data,label,test_size=0.2,random_state = 0)
    print(traindata.shape,trainlabel.shape,valdata.shape,vallabel.shape)

    n = net()
    n.fit(traindata, trainlabel)

    test_data = test_data.values
    predicts = n.predict(test_data)

    # save as csv file
    samples = samples_data['ImageId']
    result = {'ImageId':samples,
              'Label': predicts }
    result = pd.DataFrame(result)

    result.to_csv('./mnist_simple.csv', index=False)

最终的准确率：



已经0.85+了，😀，不含增量学习的bls相比之下提高了0.08的准确率。

这其实也差不多说明不含增量学习的bls其实并非十分高级，增量学习才是bls的核心。

4.4：含增量学习的MNIST结果

只是简单的添加了增量学习，并没有任何的优化，所以成绩也没有很大的提升。