题目及测试
package pid218;
/*天际线问题
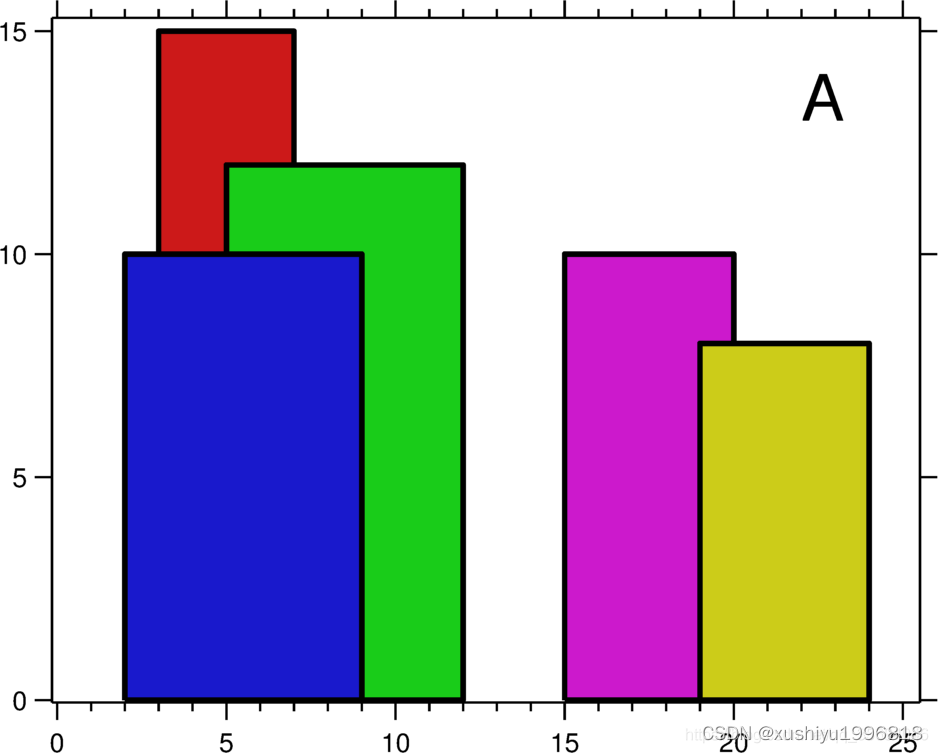
城市的天际线是从远处观看该城市中所有建筑物形成的轮廓的外部轮廓。现在,假设您获得了城市风光照片(图A)上显示的所有建筑物的位置和高度,请编写一个程序以输出由这些建筑物形成的天际线(图B)。
Buildings Skyline Contour
https://leetcode-cn.com/problems/the-skyline-problem/
每个建筑物的几何信息用三元组 [Li,Ri,Hi] 表示,其中 Li 和 Ri 分别是第 i 座建筑物左右边缘的 x 坐标,Hi 是其高度。可以保证 0 ≤ Li, Ri ≤ INT_MAX, 0 < Hi ≤ INT_MAX 和 Ri - Li > 0。您可以假设所有建筑物都是在绝对平坦且高度为 0 的表面上的完美矩形。
例如,图A中所有建筑物的尺寸记录为:[ [2 9 10], [3 7 15], [5 12 12], [15 20 10], [19 24 8] ] 。
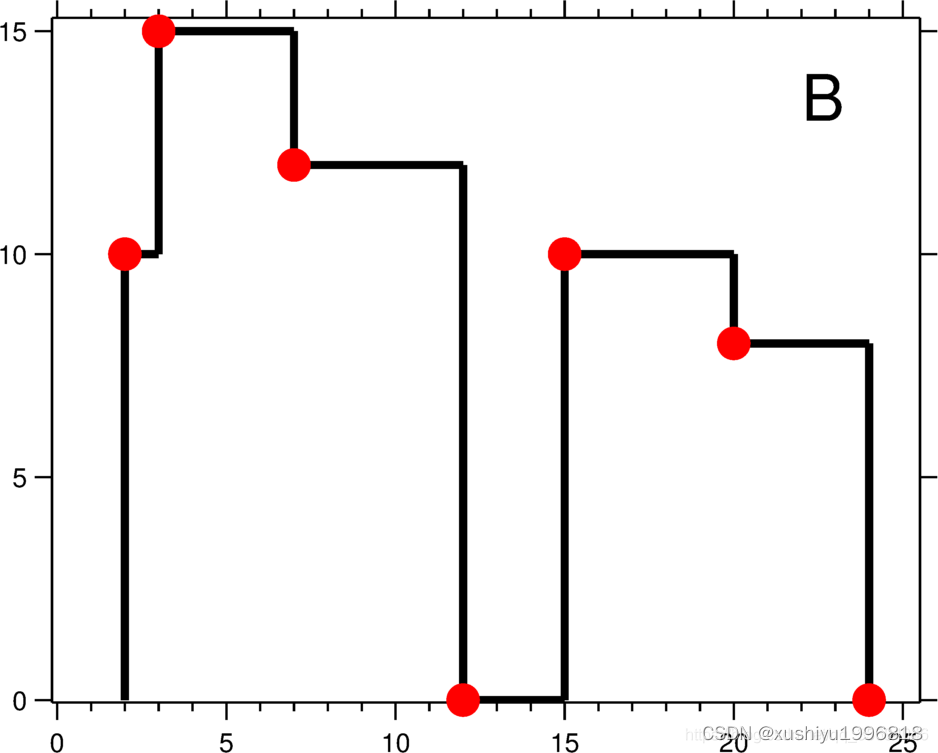
输出是以 [ [x1,y1], [x2, y2], [x3, y3], ... ] 格式的“关键点”(图B中的红点)的列表,它们唯一地定义了天际线。关键点是水平线段的左端点。请注意,最右侧建筑物的最后一个关键点仅用于标记天际线的终点,并始终为零高度。此外,任何两个相邻建筑物之间的地面都应被视为天际线轮廓的一部分。
例如,图B中的天际线应该表示为:[ [2 10], [3 15], [7 12], [12 0], [15 10], [20 8], [24, 0] ]。
说明:
任何输入列表中的建筑物数量保证在 [0, 10000] 范围内。
输入列表已经按左 x 坐标 Li 进行升序排列。
输出列表必须按 x 位排序。
输出天际线中不得有连续的相同高度的水平线。例如 [...[2 3], [4 5], [7 5], [11 5], [12 7]...] 是不正确的答案;三条高度为 5 的线应该在最终输出中合并为一个:[...[2 3], [4 5], [12 7], ...]
*/
import java.util.List;
public class main {
public static void main(String[] args) {
int[][] testTable = {{1, 2, 3, 4},{5, 6, 7, 8},{9,10,11,12}};
test(testTable);
}
private static void test(int[][] ito) {
Solution solution = new Solution();
List<List<Integer>> rtn;
long begin = System.currentTimeMillis();
for(int i=0;i<ito.length;i++){
for(int j=0;j<ito[0].length;j++){
System.out.print( ito[i][j]+" ");
}
System.out.println();
}
System.out.println();
//开始时打印数组
rtn = solution.getSkyline(ito);//执行程序
long end = System.currentTimeMillis();
System.out.println( "rtn=" );
for(int i=0;i<rtn.size();i++){
for(int j=0;j<rtn.get(i).size();j++){
System.out.print( rtn.get(i).get(j)+" ");
}
System.out.println();
}
System.out.println();
System.out.println("耗时:" + (end - begin) + "ms");
System.out.println("-------------------");
}
}
自己没想出来
解法1(别人的)
方法:分治
这个题是一道经典的分治算法题,通常如同归并排序一样。
我们依据下面的算法流程来求解分治问题:
定义基本问题。
将问题分解为子问题,并递归地分别求解。
将子问题合并成原问题的解。
算法
求解 n 栋楼的天际线:
如果 n == 0:返回一个空列表
如果 n == 1:返回一栋楼的天际线
leftSkyline = 求解前 n/2 栋楼的天际线。
rightSkyline = 求解后 n/2 栋楼的天际线。
合并 leftSkyline 和 rightSkyline.
现在,让我们进一步讨论每一个步骤的细节:
基本问题
最基本的情况就是建筑物列表为空,此时天际线也是一个空列表。
第二种基本情况就是列表中只有一栋楼,天际线是很显然的。

如何拆分问题
与归并排序的想法类似:在每一步将列表恰好拆分成两个部分:从
0
到
n/2
和
n/2
到
n
,对每一部分分别求解天际线。

如何合并两部分的天际线
合并的过程十分直接明了,基于相同的归并排序的逻辑:结果天际线的高度永远是左天际线和右天际线的较大值。

我们这里用两个指针 pR 和 pL 分别记录两个天际线的当前元素,再用三个整数变量 leftY,rightY 和 currY 分别记录 左 天际线、 右 天际线和 合并 天际线的当前高度。
mergeSkylines (left, right) :
currY = leftY = rightY = 0
当我们在一段两个天际线都可以见到的区域时(pR < nR 且 pL < nL):
选择 x 坐标较小的一个元素,如果它是左天际线的元素,就移动 pL 同时更新 leftY 。如果是右天际线,则移动 pR 且更新 rightY 。
计算较高的高度作为当前点的高度:maxY = max(leftY, rightY) 。
更新结果天际线: (x, maxY),前提是 maxY 不等于 currY.
如果左天际线还有元素没有被处理,也就是(pL < nL),则按照上述步骤处理这些元素。
如果右天际线还有元素没有被处理,也就是(pR < nR),则按照上述步骤处理这些元素。
返回结果天际线。
这里有 3 个样例来说明合并算法的过程。


class Solution {
/**
* Divide-and-conquer algorithm to solve skyline problem,
* which is similar with the merge sort algorithm.
*/
public List<List<Integer>> getSkyline(int[][] buildings) {
int n = buildings.length;
List<List<Integer>> output = new ArrayList<List<Integer>>();
// The base cases
if (n == 0) return output;
if (n == 1) {
int xStart = buildings[0][0];
int xEnd = buildings[0][1];
int y = buildings[0][2];
output.add(new ArrayList<Integer>() {{add(xStart); add(y); }});
output.add(new ArrayList<Integer>() {{add(xEnd); add(0); }});
// output.add(new int[]{xStart, y});
// output.add(new int[]{xEnd, 0});
return output;
}
// If there is more than one building,
// recursively divide the input into two subproblems.
List<List<Integer>> leftSkyline, rightSkyline;
leftSkyline = getSkyline(Arrays.copyOfRange(buildings, 0, n / 2));
rightSkyline = getSkyline(Arrays.copyOfRange(buildings, n / 2, n));
// Merge the results of subproblem together.
return mergeSkylines(leftSkyline, rightSkyline);
}
/**
* Merge two skylines together.
*/
public List<List<Integer>> mergeSkylines(List<List<Integer>> left, List<List<Integer>> right) {
int nL = left.size(), nR = right.size();
int pL = 0, pR = 0;
int currY = 0, leftY = 0, rightY = 0;
int x, maxY;
List<List<Integer>> output = new ArrayList<List<Integer>>();
// while we're in the region where both skylines are present
while ((pL < nL) && (pR < nR)) {
List<Integer> pointL = left.get(pL);
List<Integer> pointR = right.get(pR);
// pick up the smallest x
if (pointL.get(0) < pointR.get(0)) {
x = pointL.get(0);
leftY = pointL.get(1);
pL++;
}
else {
x = pointR.get(0);
rightY = pointR.get(1);
pR++;
}
// max height (i.e. y) between both skylines
maxY = Math.max(leftY, rightY);
// update output if there is a skyline change
if (currY != maxY) {
updateOutput(output, x, maxY);
currY = maxY;
}
}
// there is only left skyline
appendSkyline(output, left, pL, nL, currY);
// there is only right skyline
appendSkyline(output, right, pR, nR, currY);
return output;
}
/**
* Update the final output with the new element.
*/
public void updateOutput(List<List<Integer>> output, int x, int y) {
// if skyline change is not vertical -
// add the new point
if (output.isEmpty() || output.get(output.size() - 1).get(0) != x)
output.add(new ArrayList<Integer>() {{add(x); add(y); }});
// if skyline change is vertical -
// update the last point
else {
output.get(output.size() - 1).set(1, y);
}
}
/**
* Append the rest of the skyline elements with indice (p, n)
* to the final output.
*/
public void appendSkyline(List<List<Integer>> output, List<List<Integer>> skyline,
int p, int n, int currY) {
while (p < n) {
List<Integer> point = skyline.get(p);
int x = point.get(0);
int y = point.get(1);
p++;
// update output
// if there is a skyline change
if (currY != y) {
updateOutput(output, x, y);
currY = y;
}
}
}
}
解法2(别人的)
首先要画出轮廓线,其实就是画轮廓点,而轮廓点显示就是在建筑的左上右上顶点中,问题转化为找符合条件的顶点。
每个没被遮挡的高建筑左顶点一定是轮廓点;高建筑和矮建筑交汇的地方,取的是高建筑右顶点的横坐标和矮建筑的高度作为轮廓点;每一片连在一起的建筑的最右边的轮廓点,纵坐标取0
这题网上最主流的解法是用大顶堆来解,看了很久才理解,这里尝试解释一下:
将每条建筑的横线段分解成左上右上两个顶点,将所有这些点按横坐标大小升序排列
从左至右遍历这些点,每遍历到一个左顶点,将此点代表的建筑高度放入大顶堆height中
每次到一个左顶点,先比较此顶点高度与当前基准高度,如果高于基准高度,那么就是一个轮廓点。这是最关键的地方,结合图形理解,如果当前建筑的左顶点要作比较,肯定是与它前面有重叠的建筑比较,而前面重叠的建筑高度,要取之前最高的、横线还在延续的建筑比较,因此需要用到一个大顶堆维护当前高度
还有两个细节:
1. 将右顶点的高度设为负值,在遍历点时用以区分左右顶点
2. 碰到左顶点将高度加入大顶堆,碰到右顶点时,说明此建筑横向的延绵结束了,那么要从大顶堆中删掉此高度
public List<int[]> getSkyline(int[][] buildings) {
List<int[]> list = new ArrayList<int[]>();
Set<int []>set = new TreeSet<int[]>(new Comparator<int[]>() {
@Override
public int compare(int[] o1, int[] o2) {//每个顶点先横坐标排序
if(o1[0] == o2[0]){//横坐标相同时,纵坐标要降序排列
return o2[1] - o1[1];
}
return o1[0] - o2[0];
}
});
//高度降序优先队列(大顶堆)
PriorityQueue<Integer> height = new PriorityQueue<Integer>(11,new Comparator<Integer>() {
@Override
public int compare(Integer o1, Integer o2) {
return o2-o1;
}
});
//构造顶点横坐标升序set
for(int i=0;i<buildings.length;i++){
int[] A = {buildings[i][0],buildings[i][2]};
set.add(A);
//右顶点y值设为负值,便于区分
int[] B = {buildings[i][1],-1*buildings[i][2]};
set.add(B);
}
//遍历set
height.offer(0);
int preHeight = 0;
for(int[] A : set){
if(A[1] > 0){//左顶点
if(A[1] > preHeight){//左顶点大于上一高度
list.add(A);
}
height.offer(A[1]);//加入当前线段高度
preHeight = height.peek();//拿顶部元素作为上次高度
}
else{
height.remove(-1*A[1]);//右顶点时去掉大顶堆对应左顶点
preHeight = height.peek();//拿顶部元素作为上次高度
if(-1*A[1] > preHeight){//右顶点大于上一高度
int []temp = {A[0],preHeight};
list.add(temp);
}
}
}
return list;
}解法3(别人的)
其实说到底这个题在每一个位置都需要我们掌握的是在这个位置的现任大哥是谁,以及之前的位置的大哥(简称过去式大哥),当然评选大哥的标准很简单,便是谁长的 更高大!
数据结构:
一个 Treemap<Integer,List<int[]>>
一个 PriorityQueue (优先队列)存储建筑(一个包括左右坐标以及长度的数组),高度高的在上面,所以我们加一个Comparator。
最后加上一个 List<List<< Integer >> res (返回的答案)
(选择好的数据结构可以让问题解决的更快!)
具体过程如下 :
我们将每个点以及它对应的建筑加入treemap中,如果该点是一个建筑的起点,则加入优先队列,否则从优先队列中删除。
随后,我们从优先队列中获取当前的大哥,与过去式大哥进行比较,如果大哥变化了,我们便将新大哥节点加入res中(当然如果res里什么都没有存储,则直接将其加入res即可)。
如果遇到优先队列为空则说明,我们遍历完了一部分连在一起的建筑,将当前点和0加入res即可。
public class Solution2 {
public List<List<Integer>> getSkyline(int[][] buildings) {
List<List<Integer>> res = new ArrayList<>();//存放结果的res
PriorityQueue<int[]> maxHeap = new PriorityQueue<>((a,b)->b[2]-a[2]);//存放
TreeMap<Integer,List<int[]>> map = new TreeMap<>();
for(int[] b:buildings) {//将所有数据全部放入map中
map.putIfAbsent(b[0], new ArrayList<int[]>());
map.putIfAbsent(b[1], new ArrayList<int[]>());
map.get(b[0]).add(b);
map.get(b[1]).add(b);
}
for(int a:map.keySet()) {
List<int[]> bs = map.get(a);
for(int[] b:bs) {
if(b[0] == a) {
maxHeap.offer(b);
}else {
maxHeap.remove(b);
}
}
if(maxHeap.size()==0) {
List<Integer> temp = new ArrayList<>();
temp.add(a);
temp.add(0);
res.add(temp);
}else {
int maxHeight = maxHeap.peek()[2];
if(res.size() == 0||res.get(res.size()-1).get(1)!=maxHeight) {
List<Integer> temp = new ArrayList<>();
temp.add(a);
temp.add(maxHeight);
res.add(temp);
}
}
}
return res;
}