LeetCode链接
一、问题描述
有 n 个气球,编号为0 到 n-1,每个气球上都标有一个数字,这些数字存在数组 nums 中。
现在要求你戳破所有的气球。每当你戳破一个气球 i 时,你可以获得 nums[left] * nums[i] * nums[right] 个硬币。 这里的 left 和 right 代表和 i 相邻的两个气球的序号。注意当你戳破了气球 i 后,气球 left 和气球 right 就变成了相邻的气球。
求所能获得硬币的最大数量。
说明:
你可以假设 nums[-1] = nums[n] = 1,但注意它们不是真实存在的所以并不能被戳破。
0 ≤ n ≤ 500, 0 ≤ nums[i] ≤ 100
示例:

二、问题分析以及代码
这种问题看起来就很棘手QAQ,冷静下来思考。
1. 回溯法
一个非常朴素的想法,就是穷举所有戳爆气球的情况,记录其最大得分值。
class Solution:
def maxCoins(self, nums: List[int]) -> int:
self.res = 0
nums = [1] + nums + [1] # 数组左右两边补值
self.dfs(nums, 0, 1, len(nums)-2) # 遍历[1, len(nums)-2]区间所有戳气球的方法
return self.res
def dfs(self, nums, cur, left, right):
if left>right: # 边界条件
self.res = max(self.res, cur)
for i in range(left, right+1):
self.dfs(nums[:i]+nums[i+1:], cur+nums[i]*nums[i-1]*nums[i+1], 1, len(nums)-3) # 回溯
易知递归调用的次数为 n!+(n-1)!+…+1! 次,这是非常庞大的,而题目的n上界为500,显然这样提交会超时。
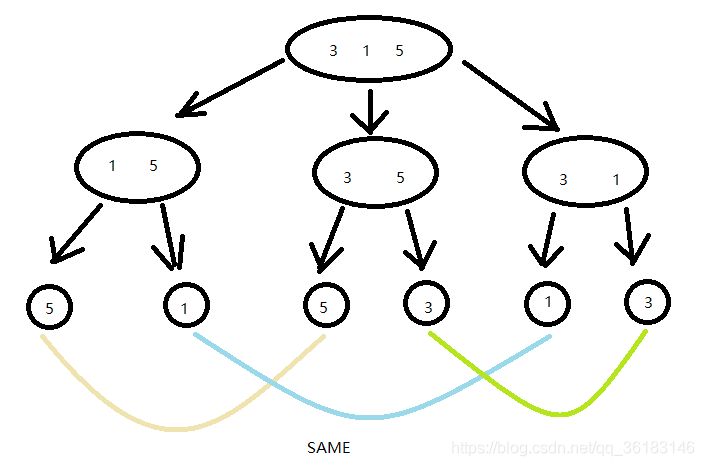
而且由上图可见有很多问题是被
递归重复计算
的,由此引入记忆化方法。
2. 记忆化搜索
正向思维:戳爆一个气球,剩余气球合并,这样原本的左右由于合并后面继续戳爆左右会有交互,所以
并不独立
。
但换一种思考方式:先选定一个气球最后戳爆,
优先
将其气球左右两边的气球戳爆,这样就能将左右两边的问题独立开。
具体过程
设置一个数组
dp[i][j]
, 它表示区间戳爆区间
[i, j]
的气球所能获得的最大分数,
选择
k∈[i, j]
,当前得到的分数为
左区间最大分数
+
右区间最大分数
+
戳爆该点得到的分数
:
cur = dp[i][k-1] + dp[k+1][j] + nums[i-1]*nums[j+1]*nums[k]
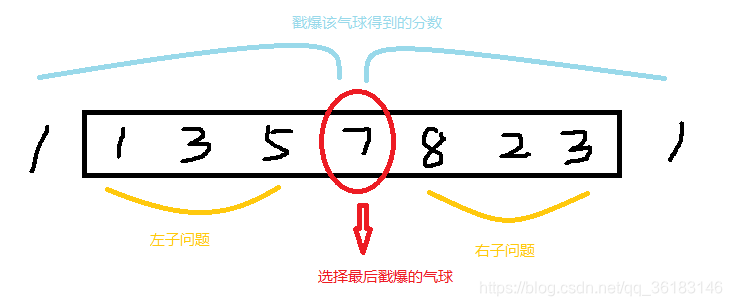
遍历所有的k取最大值就是该区间能获得的最大分数。
这样我们就能记录固定区间的最大分数,若有重复计算直接查值即可。
代码(Python)
class Solution:
def maxCoins(self, nums) -> int:
if len(nums):
return 0
nums = [1] + nums + [1]
n = len(nums)
self.dp = [[-1 for i in range(n)] for j in range(n)]
return self.dfs(nums, 1, n-2)
def dfs(self, nums, left, right):
if left>right:
return 0
if self.dp[left][right]!=-1:
return self.dp[left][right]
for i in range(left, right+1):
cur = self.dfs(nums, left, i-1) + self.dfs(nums, i+1, right) + nums[i]*nums[left-1]*nums[right+1]
self.dp[left][right] = max(self.dp[left][right], cur)
return self.dp[left][right]
这样调用次数就是为填表的次数,大大减少。
3. 动态规划
上述问题都是先计算小区间再积累到大区间,
也即长度为n区间的得分值是通过长度小于等于n-1区间的得分值计算出来的。
我们完全可以不用递归。先设置一个区间长度,起始为1,计算再该长度下的区间能够都得到的最大值,然后长度自增,逐步计算。
代码(Python)
class Solution:
def maxCoins(self, nums: List[int]) -> int:
if len(nums)==0:
return 0
n = len(nums)
nums = [1] + nums + [1]
dp = [[0 for i in range(n+2)] for j in range(n+2)]
for length in range(1, n+1): # 区间长度的范围
for i in range(1, n-length+2): # 区间的起始点
j = i+length-1 # 区间的终点
for k in range(i, j+1):
dp[i][j] = max(dp[i][j], dp[i][k-1]+dp[k+1][j]+nums[k]*nums[i-1]*nums[j+1])
return dp[1][n]
三、思考
对于递归问题,尝试思考是否能够分成多个独立的子问题,通过记忆化的方法避免重复计算从而降低复杂度。