支持向量机之线性可分向量机

一、支持向量机简介

支持向量机（support vector machines，SVM）是一种二类分类模型。它的基本模型是定义在特征空间上的间隔最大的线性分类器，间隔最大使它有别于感知机；支持向量机还包括核技巧，这使它成为实质上的非线性分类器。当训练数据线性可分时，通过硬间隔最大化（hard margin maximization），学习一个线性的分类器，即线性可分支持向量机，又称为硬间隔支持向量机；当训练数据近似线性可分时，通过软间隔最大化（soft margin maximization），也学习一个线性的分类器，即线性支持向量机，又称为软间隔支持向量机；当训练数据线性不可分时，通过使用核技巧（kernel trick）及软间隔最大化，学习非线性支持向量机。

二、函数间隔和集合间隔

支持向量机通过样本距离超平面的距离来衡量预测的确定性或者准确性；例如下边的图中，A点预测的确信度相对B和C更大；

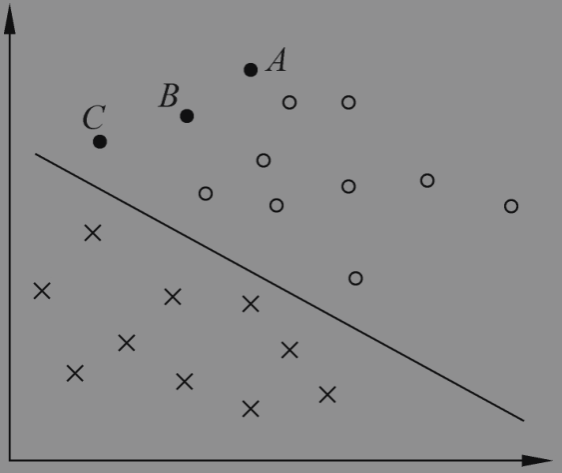
我们设最终确定的分离超平面为

wx+b = 0

$w x + b = 0$

我们设

y = 1

$y = 1$

表示正类，

−

y = -1

$y = - 1$

表示负类，相应的分类决策函数为

(

)

sign

⁡

(

∗

⋅

∗

)

f(x)=\operatorname{sign}\left(w^{*} \cdot x+b^{*}\right)

$f (x) = s i g n (w^{*} \cdot x + b^{*})$

则样本点

)

(x_{i}, y_{i})

$(x_{i}, y_{i})$

到分割超平面的距离称为函数距离

(

⋅

)

\hat{\gamma}_{i}=y_{i}\left(w \cdot x_{i}+b\right)

$\overset{γ}{^}_{i} = y_{i} (w \cdot x_{i} + b)$

则训练集关于超平面的函数间隔为所有样本点中函数间隔最小的值

min

⁡

⋯

\hat{\gamma}=\min _{i=1, \cdots, N} \hat{\gamma}_{i}

$\overset{γ}{^} = i = 1, \dots, N min \overset{γ}{^}_{i}$

虽然函数间隔可以表征分类预测的正确性和确认度，但是由于同一个超平面存在不同的参数组合，导致函数距离不唯一，所以我们需要对超平面的法向量进行归一化，从而得到几何间隔

(

∥

⋅

∥

)

\gamma_{i}=y_{i}\left(\frac{w}{\|w\|} \cdot x_{i}+\frac{b}{\|w\|}\right)

$γ_{i} = y_{i} (\frac{w}{∥ w ∥} \cdot x_{i} + \frac{b}{∥ w ∥})$

同样训练集关于超平面的几何间隔为所有样本点中几何间隔最小的值

min

⁡

⋯

\gamma=\min _{i=1, \cdots, N} \gamma_{i}

$γ = i = 1, \dots, N min γ_{i}$

三、几何间隔最大化

对训练数据集找到几何间隔最大的超平面意味着以充分大的确信度对训练数据进行分类。也就是说，不仅将正负实例点分开，而且对最难分的实例点（离超平面最近的点）也有足够大的确信度将它们分开。这样的超平面应该对未知的新实例有很好的分类预测能力。

几何间隔最大化，即我们希望最大化超平面

)

(w, b)

$(w, b)$

关于训练数据集的几何间隔

\gamma

$γ$

，约束条件表示的是超平面

)

(w, b)

$(w, b)$

关于每个训练样本点的几何间隔至少是

\gamma

$γ$

⁡

s.t.

(

∥

⋅

∥

)

⩾

⋯

\begin{array}{ll} \max _{w, b} & \gamma \\ \text { s.t. } & y_{i}\left(\frac{w}{\|w\|} \cdot x_{i}+\frac{b}{\|w\|}\right) \geqslant \gamma, \quad i=1,2, \cdots, N \end{array}

$max_{w, b} s.t. γ y_{i} (\frac{w}{∥ w ∥} \cdot x_{i} + \frac{b}{∥ w ∥}) ⩾ γ, i = 1, 2, \dots, N$

使用函数距离替换集合距离

⁡

∥

s.t.

(

⋅

)

⩾

⋯

\begin{array}{ll} \max _{w, b} & \frac{\hat{\gamma}}{\|w\|} \\ \text { s.t. } & y_{i}\left(w \cdot x_{i}+b\right) \geqslant \hat{\gamma}, \quad i=1,2, \cdots, N \end{array}

$max_{w, b} s.t. \frac{γ ^}{∥ w ∥} y_{i} (w \cdot x_{i} + b) ⩾ \overset{γ}{^}, i = 1, 2, \dots, N$

由于超平面的两个参数可以成比例的随意变化，导致函数距离可以取任何值，但是最终结果并不影响约束条件和目标函数，故我们直接取

\hat{\gamma}=1

$\overset{γ}{^} = 1$

，同时将最大化改为最小化，则最优化问题变为

⁡

∥

s.t.

(

⋅

)

−

⩾

⋯

\begin{array}{ll} \min _{w, b} & \frac{1}{2}\|w\|^{2} \\ \text { s.t. } & y_{i}\left(w \cdot x_{i}+b\right)-1 \geqslant 0, \quad i=1,2, \cdots, N \end{array}

$min_{w, b} s.t. \frac{1}{2} ∥ w ∥^{2} y_{i} (w \cdot x_{i} + b) - 1 ⩾ 0, i = 1, 2, \dots, N$

如果我们计算得到这个最优化问题的解

∗

w^*,b^*

$w^{*}, b^{*}$

,那么我们就得到了分离超平面和分类决策函数；

四、支持向量

在线性可分情况下，训练数据集的样本点中与分离超平面距离最近的样本点的实例称为支持向量（support vector）。在决定分离超平面时只有支持向量起作用，而其他实例点并不起作用。如果移动支持向量将改变所求的解；但是如果在间隔边界以外移动其他实例点，甚至去掉这些点，则解是不会改变的。由于支持向量在确定分离超平面中起着决定性作用，所以将这种分类模型称为支持向量机。支持向量的个数一般很少，所以支持向量机由很少的“重要的”训练样本确定。

五、通过对偶算法求解最大化间隔

为了求解线性可分支持向量机的最优化问题，将它作为原始最优化问题，应用拉格朗日对偶性原始问题的最优解，这就是线性可分支持向量机的对偶算法（dual algorithm）。

通过引入拉格朗日乘子构建拉格朗日函数

(

)

∥

−

∑

(

⋅

)

∑

L(w, b, \alpha)=\frac{1}{2}\|w\|^{2}-\sum_{i=1}^{N} \alpha_{i} y_{i}\left(w \cdot x_{i}+b\right)+\sum_{i=1}^{N} \alpha_{i}

$L (w, b, α) = \frac{1}{2} ∥ w ∥^{2} - i = 1 \sum N α_{i} y_{i} (w \cdot x_{i} + b) + i = 1 \sum N α_{i}$

根据拉格朗日对偶性，原始问题的对偶问题是极大极小问题

⁡

min

⁡

(

)

\max _{\alpha} \min _{w, b} L(w, b, \alpha)

$α max w, b min L (w, b, α)$

分别对两个参数计算偏导计算极小值

(

)

−

∑

∇

(

)

−

∑

\begin{array}{l} \nabla_{w} L(w, b, \alpha)=w-\sum_{i=1}^{N} \alpha_{i} y_{i} x_{i}=0 \\ \nabla_{b} L(w, b, \alpha)=-\sum_{i=1}^{N} \alpha_{i} y_{i}=0 \end{array}

$\nabla_{w} L (w, b, α) = w - \sum_{i = 1}^{N} α_{i} y_{i} x_{i} = 0 \nabla_{b} L (w, b, α) = - \sum_{i = 1}^{N} α_{i} y_{i} = 0$

计算得到

∑

\begin{array}{l} w=\sum_{i=1}^{N} \alpha_{i} y_{i} x_{i} \\ \sum_{i=1}^{N} \alpha_{i} y_{i}=0 \end{array}

$w = \sum_{i = 1}^{N} α_{i} y_{i} x_{i} \sum_{i = 1}^{N} α_{i} y_{i} = 0$

将其带入上边构建的拉格朗日函数

(

)

∑

(

⋅

)

−

∑

(

∑

)

⋅

)

∑

−

∑

(

⋅

)

∑

\begin{aligned} L(w, b, \alpha) &=\frac{1}{2} \sum_{i=1}^{N} \sum_{j=1}^{N} \alpha_{i} \alpha_{j} y_{i} y_{j}\left(x_{i} \cdot x_{j}\right)-\sum_{i=1}^{N} \alpha_{i} y_{i}\left(\left(\sum_{j=1}^{N} \alpha_{j} y_{j} x_{j}\right) \cdot x_{i}+b\right)+\sum_{i=1}^{N} \alpha_{i} \\ &=-\frac{1}{2} \sum_{i=1}^{N} \sum_{j=1}^{N} \alpha_{i} \alpha_{j} y_{i} y_{j}\left(x_{i} \cdot x_{j}\right)+\sum_{i=1}^{N} \alpha_{i} \end{aligned}

$L (w, b, α) = \frac{1}{2} i = 1 \sum N j = 1 \sum N α_{i} α_{j} y_{i} y_{j} (x_{i} \cdot x_{j}) - i = 1 \sum N α_{i} y_{i} ((j = 1 \sum N α_{j} y_{j} x_{j}) \cdot x_{i} + b) + i = 1 \sum N α_{i} = - \frac{1}{2} i = 1 \sum N j = 1 \sum N α_{i} α_{j} y_{i} y_{j} (x_{i} \cdot x_{j}) + i = 1 \sum N α_{i}$

接下来计算最大值部分

⁡

−

∑

(

⋅

)

∑

s.t.

∑

⩾

⋯

\begin{array}{ll} \max _{\alpha} & -\frac{1}{2} \sum_{i=1}^{N} \sum_{j=1}^{N} \alpha_{i} \alpha_{j} y_{i} y_{j}\left(x_{i} \cdot x_{j}\right)+\sum_{i=1}^{N} \alpha_{i} \\ \text { s.t. } & \sum_{i=1}^{N} \alpha_{i} y_{i}=0 \\ & \alpha_{i} \geqslant 0, \quad i=1,2, \cdots, N \end{array}

$max_{α} s.t. - \frac{1}{2} \sum_{i = 1}^{N} \sum_{j = 1}^{N} α_{i} α_{j} y_{i} y_{j} (x_{i} \cdot x_{j}) + \sum_{i = 1}^{N} α_{i} \sum_{i = 1}^{N} α_{i} y_{i} = 0 α_{i} ⩾ 0, i = 1, 2, \dots, N$

转化为等效的计算极小问题

⁡

∑

(

⋅

)

−

∑

s.t.

∑

⩾

⋯

\begin{array}{ll} \min _{\alpha} & \frac{1}{2} \sum_{i=1}^{N} \sum_{j=1}^{N} \alpha_{i} \alpha_{j} y_{i} y_{j}\left(x_{i} \cdot x_{j}\right)-\sum_{i=1}^{N} \alpha_{i} \\ \text { s.t. } \quad \sum_{i=1} \alpha_{i} y_{i}=0 \\ \alpha_{i} \geqslant 0, \quad i=1,2, \cdots, N \end{array}

$min_{α} s.t. \sum_{i = 1} α_{i} y_{i} = 0 α_{i} ⩾ 0, i = 1, 2, \dots, N \frac{1}{2} \sum_{i = 1}^{N} \sum_{j = 1}^{N} α_{i} α_{j} y_{i} y_{j} (x_{i} \cdot x_{j}) - \sum_{i = 1}^{N} α_{i}$

对线性可分训练数据集，假设对偶最优化问题对α的解为

∗

(

∗

⋯

∗

)

\alpha^{*}=\left(\alpha_{1}^{*}, \alpha_{2}^{*}, \cdots, \alpha_{l}^{*}\right)^{\mathrm{T}}

$α^{*} = (α_{1}^{*}, α_{2}^{*}, \dots, α_{l}^{*})^{T}$

则存在下标j，使得

∗

\alpha_{j}^{*}>0

$α_{j}^{*} > 0$

，并可按下式求得原始最优化问题的解

∗

w^{*}, b^{*}

$w^{*}, b^{*}$

∗

∑

∗

−

∑

∗

(

⋅

)

\begin{array}{l} w^{*}=\sum_{i=1}^{N} \alpha_{i}^{*} y_{i} x_{i} \\ b^{*}=y_{j}-\sum_{i=1}^{N} \alpha_{i}^{*} y_{i}\left(x_{i} \cdot x_{j}\right) \end{array}

$w^{*} = \sum_{i = 1}^{N} α_{i}^{*} y_{i} x_{i} b^{*} = y_{j} - \sum_{i = 1}^{N} α_{i}^{*} y_{i} (x_{i} \cdot x_{j})$

由此可得分离超平面

∗

(

⋅

)

∗

\sum_{i=1}^{N} \alpha_{i}^{*} y_{i}\left(x \cdot x_{i}\right)+b^{*}=0

$i = 1 \sum N α_{i}^{*} y_{i} (x \cdot x_{i}) + b^{*} = 0$

可得分类决策函数

(

)

sign

⁡

(

∑

∗

(

⋅

)

∗

)

f(x)=\operatorname{sign}\left(\sum_{i=1}^{N} \alpha_{i}^{*} y_{i}\left(x \cdot x_{i}\right)+b^{*}\right)

$f (x) = s i g n (i = 1 \sum N α_{i}^{*} y_{i} (x \cdot x_{i}) + b^{*})$

可以看到线性可分支持向量机的对偶形式只依赖于输入x和训练样本输入的内积。通过上边

∗

w^{*}, b^{*}

$w^{*}, b^{*}$

的表达式，可以看到两个参数只依赖

∗

\alpha_{j}^{*}>0

$α_{j}^{*} > 0$

对应的训练样本点，这些样本点就是支持向量；

六、算法示例

from sklearn.datasets import load_iris
from sklearn.svm import LinearSVC
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler

x, y = load_iris(return_X_y= True)
svc = Pipeline([
    ('scaler',StandardScaler()),
    ('linear_svc', LinearSVC(C=float('inf'), loss='hinge'))
])
svc = svc.fit(x, y)
print(svc.predict(x))
print(svc.score(x, y))

# [0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
#  0 0 0 0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
#  1 1 1 1 1 1 1 1 1 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 2 2 2 2 2 2 2 2 2
#  2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 1 2 2 2 2 2 2 2 2 2 2 2 2 2 2
#  2 2]
# 0.9866666666666667

原文链接：https://blog.csdn.net/hou478410969/article/details/124467577

你可能也喜欢