1.2 无向图的深度优先遍历
DFS:Depth First Search
算法思想
:1、以一个未被访问过的顶点作为起始顶点,沿当前顶点的的边走向未被访问过的顶点;2、执行1步骤后,当该分支结点都被访问后,则返回到上一个顶点,继续检索其他未被访问过的顶点,直至所有的顶点都被访问过。
即
一路走到底,不破南墙不回头//这里简称直男思维。
以下图“无向图”为例:
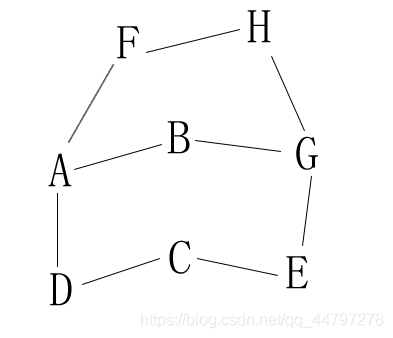
假设从A顶点,按照
字母先后
,开始进行深度遍历:
A -> B -> G -> E -> C -> D -> H -> F,深度优先遍历类似于二叉树的先序遍历。
1、访问A。 2、访问B,邻接点。3、访问G,邻接点,因为B除了A-B边,剩下 B-G这条边。
4、访问E,邻接点,字母顺序。
注,G相当于一颗二叉树,一个分支顶点被访问完就会回到这里继续检索另外一个分支。
5、访问C,邻接点,同B-G边。6、访问D,邻接点,同B-G边。
7、访问H,因为D周围的顶点=被访问了,所有此时开始回溯到G顶点,继续检索到H
8、访问F,同B-G边。 ———-结束
1.2 有向图的深度优先遍历
有向图的深度优先遍历图解:
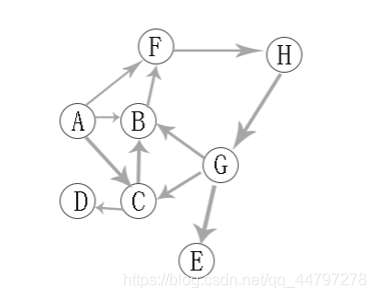
A -> B -> F -> H -> G -> C -> D -> E
与无向图大致相仿,检索未被访问的顶点,检索+回溯,这里不做详细说明。
2.1 图的广度优先遍历
直接放图:

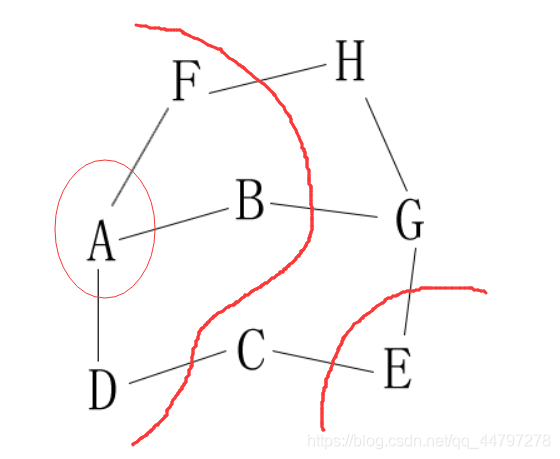
A -> D -> B -> F -> C -> G -> H -> E
图的广度优先遍历比较好理解,将相同层次的临界点划分在一个层次。
由2图可知,A的邻接点为 DBF ,所以 A -> D -> B -> F,而D未被访问的邻接点 只有C,B未被访问的邻接点只有G,F未被访问的邻接点只有H 所以:A -> D -> B -> F -> C -> G -> H , 而剩下最后一顶点 E 自动补充上去。就是改图的广度优先遍历。
总结:图的深度优先遍历算法先访问所在结点,在访问它的邻接点。与二叉树的先序遍历(先访问子树的根结点,再访问它的孩子结点)类似。图的广度优先遍历算法类似于二叉树的按层次遍历。