内容概述
本节首先从齐次线性方程组入手,研究了解集的向量形式,由此建立了
解向量
、
解空间
的思考模式;接着为了完备性,扩展到非齐次线性方程组,说明了从
向量
、
空间
的角度线性方程组解集的一般表示形式。总之,本节的重点是建立从
向量
的线性组合、
空间
的几何意义的角度来研究线性方程组的
解集
。
齐次线性方程组
线性方程组称为
齐次
的,若它可写成
A
x
=
0
A\boldsymbol x = \boldsymbol 0
A
x
=
0
的形式。其中
A
A
A
是
m
×
n
m \times n
m
×
n
矩阵而
0
\boldsymbol 0
0
是
R
m
\mathbb R^m
R
m
中的零向量(从向量的角度看,就是说
A
A
A
的各列生成了
0
\boldsymbol 0
0
向量)。
显然,齐次线性方程组至少有一个解,即
x
=
0
\boldsymbol x = \boldsymbol 0
x
=
0
,这个解称为它的
平凡解
。对给定方程
A
x
=
0
A\boldsymbol x = \boldsymbol 0
A
x
=
0
,重要的是它是否有
非平凡解
,即满足
A
x
=
0
A\boldsymbol x = \boldsymbol 0
A
x
=
0
的非零向量
0
\boldsymbol 0
0
。
回顾1.2节关于
解的存在性与唯一性
的讨论:
若线性方程组相容,则它的解集可能有两种情形:1. 当没有自由变量时,有唯一解; 2. 若至少有一个自由变量,则有无穷多解。
由上述结论,可以得知,对于齐次方程来说:
当没有自由变量时,存在唯一解,即
x=
0
\boldsymbol x = \boldsymbol 0
x
=
0
有平凡解当且仅当方程至少有一个自由变量
例:
确定下列齐次方程组是否有非平凡解,并描述它的解集:
3
x
1
+
5
x
2
−
4
x
3
=
0
−
3
x
1
−
2
x
2
+
4
x
3
=
0
6
x
1
+
x
2
−
8
x
3
=
0
\begin{aligned} 3x_1 + 5x_2 – 4x_3 = 0\\ -3x_1 – 2x_2 + 4x_3 = 0\\ 6x_1 + x_2 – 8x_3 = 0 \end{aligned}
3
x
1
+
5
x
2
−
4
x
3
=
0
−
3
x
1
−
2
x
2
+
4
x
3
=
0
6
x
1
+
x
2
−
8
x
3
=
0
解:
该方程组的系数矩阵可以化简为如下的简化阶梯形:
[
1
0
−
4
3
0
0
1
0
0
0
0
0
0
]
\begin{bmatrix} 1 & 0 & -\frac{4}{3} & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ \end{bmatrix}
⎣
⎡
1
0
0
0
1
0
−
3
4
0
0
0
0
0
⎦
⎤
由此可知,
x
1
x_1
x
1
,
x
2
x_2
x
2
是基本变量,
x
3
x_3
x
3
是自由变量。
A
x
=
0
A\boldsymbol x = \boldsymbol 0
A
x
=
0
的通解可以写成如下向量形式:
x
=
[
x
1
x
2
x
3
]
=
[
4
3
x
3
0
x
3
]
=
x
3
[
4
3
0
1
]
=
x
3
v
\boldsymbol x = \begin{bmatrix}x_1 \\ x_2 \\x_3 \end{bmatrix} = \begin{bmatrix}\frac{4}{3}x_3 \\ 0 \\x_3 \end{bmatrix} = x_3\begin{bmatrix}\frac{4}{3} \\ 0 \\ 1 \end{bmatrix} = x_3\boldsymbol v
x
=
⎣
⎡
x
1
x
2
x
3
⎦
⎤
=
⎣
⎡
3
4
x
3
0
x
3
⎦
⎤
=
x
3
⎣
⎡
3
4
0
1
⎦
⎤
=
x
3
v
其中,
v
=
[
4
3
0
1
]
\boldsymbol v = \begin{bmatrix}\frac{4}{3} \\ 0 \\ 1 \end{bmatrix}
v
=
⎣
⎡
3
4
0
1
⎦
⎤
从上面解集的向量表示,可以看出,从几何意义来看,解集是
R
3
\mathbb R^3
R
3
中通过
0
\boldsymbol 0
0
的直线,且每个解都是向量
v
\boldsymbol v
v
的倍数。

同理,若一个方程的解集有两个自由变量,例如,解集如下所示:
x
=
x
2
[
0.3
1
0
]
+
x
3
[
0.2
0
1
]
\boldsymbol x = x_2\begin{bmatrix}0.3 \\1 \\ 0 \end{bmatrix} + x_3\begin{bmatrix}0.2 \\0 \\ 1 \end{bmatrix}
x
=
x
2
⎣
⎡
0
.
3
1
0
⎦
⎤
+
x
3
⎣
⎡
0
.
2
0
1
⎦
⎤
那么,解集就是一个平面:

上述两个例子说明了,齐次方程
A
x
=
0
A\boldsymbol x = \boldsymbol 0
A
x
=
0
总可以表示为
S
p
a
n
{
v
1
,
⋯
,
v
p
}
Span\{\boldsymbol v_1, \cdots, \boldsymbol v_p\}
S
p
a
n
{
v
1
,
⋯
,
v
p
}
(
由于方程式右边全为0,因此基本变量要么是0,要么是自由变量的组合,因此解集可以拆分成以自由变量为系数的几个固定向量的和,意即解集可以表示成
R
n
\mathbb R^n
R
n
中几个固定向量的线性组合,这一思想非常重要
)。若唯一解是零向量,则解集就是
S
p
a
n
{
0
}
Span\{\boldsymbol0\}
S
p
a
n
{
0
}
。若方程
A
x
=
0
A\boldsymbol x = \boldsymbol 0
A
x
=
0
仅有一个自由变量,则解集就是通过原点的一条直线,若有两个或更多个自由变量,上述平面就是一个很好的图形说明。
参数向量的形式
上述方程组的形式,是几何表示中直线或平面的
隐式
描述,解此方程就是要找到几何表示的
显式
描述,就是说,将它作为例如上图中,
u
\boldsymbol u
u
和
v
\boldsymbol v
v
所生成的子集。形如
x
=
s
u
+
t
v
\boldsymbol x = s\boldsymbol u + t\boldsymbol v
x
=
s
u
+
t
v
的形式称为平面的
参数向量形式
。
也就是说,齐次线性方程组的解集可以写成某几个固定向量的线性组合的形式。
非齐次方程组的解
当非齐次线性方程组有许多解时,通解一般也可以表示为参数向量形式,即由一个向量加上满足对应的齐次线性方程的一些向量的任意线性组合的形式。
例:
描述
A
x
=
b
A\boldsymbol x = \boldsymbol b
A
x
=
b
的解,其中
A
=
[
3
5
−
4
−
3
−
2
4
6
1
−
8
]
A = \begin{bmatrix}3 & 5 & -4 \\-3 & -2 & 4 \\ 6 & 1 & -8 \end{bmatrix}
A
=
⎣
⎡
3
−
3
6
5
−
2
1
−
4
4
−
8
⎦
⎤
b
=
[
7
−
11
4
]
\boldsymbol b = \begin{bmatrix}7 \\-11 \\ 4 \end{bmatrix}
b
=
⎣
⎡
7
−
1
1
4
⎦
⎤
解:
对
[
A
b
]
[A\quad \boldsymbol b]
[
A
b
]
做行变换得:
[
1
0
−
4
3
−
1
0
1
0
2
0
0
0
0
]
\begin{bmatrix}1 & 0 & -\frac{4}{3} & -1 \\0 & 1 & 0 & 2 \\ 0 & 0 & 0 & 0 \end{bmatrix}
⎣
⎡
1
0
0
0
1
0
−
3
4
0
0
−
1
2
0
⎦
⎤
写成方程形式为:
x
1
−
4
3
x
3
=
−
1
x
2
=
2
0
=
0
\begin{aligned} x_1 – \frac{4}{3}x_3 = -1\\ x_2 =2\\ 0 = 0 \end{aligned}
x
1
−
3
4
x
3
=
−
1
x
2
=
2
0
=
0
因此,解集可写为:
x
=
[
x
1
x
2
x
3
]
=
[
−
1
+
4
3
x
3
2
x
3
]
=
[
−
1
2
0
]
+
[
4
3
x
3
0
x
3
]
=
[
−
1
2
0
]
+
x
3
[
4
3
0
1
]
\boldsymbol x = \begin{bmatrix}x_1 \\x_2 \\ x_3 \end{bmatrix} = \begin{bmatrix}-1+\frac{4}{3}x_3 \\2 \\ x_3 \end{bmatrix} = \begin{bmatrix}-1 \\2 \\ 0 \end{bmatrix} + \begin{bmatrix}\frac{4}{3}x_3 \\0 \\ x_3 \end{bmatrix} = \begin{bmatrix}-1 \\2 \\ 0 \end{bmatrix} + x_3\begin{bmatrix}\frac{4}{3} \\0 \\ 1 \end{bmatrix}
x
=
⎣
⎡
x
1
x
2
x
3
⎦
⎤
=
⎣
⎡
−
1
+
3
4
x
3
2
x
3
⎦
⎤
=
⎣
⎡
−
1
2
0
⎦
⎤
+
⎣
⎡
3
4
x
3
0
x
3
⎦
⎤
=
⎣
⎡
−
1
2
0
⎦
⎤
+
x
3
⎣
⎡
3
4
0
1
⎦
⎤
方程可写为如下形式:
x
=
p
+
t
v
\boldsymbol x = \boldsymbol p + t\boldsymbol v
x
=
p
+
t
v
其中
A
x
=
0
A\boldsymbol x = 0
A
x
=
0
的解集有如下的参数向量形式:
x
=
t
v
\boldsymbol x = t\boldsymbol v
x
=
t
v
向量
p
\boldsymbol p
p
本身可作为
A
x
=
b
A\boldsymbol x = \boldsymbol b
A
x
=
b
的一个特解(对应
t
=
0
t=0
t
=
0
)
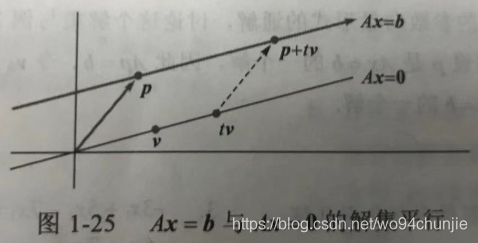
从几何意义来看,若直线
L
L
L
上每一点被平移
p
\boldsymbol p
p
,就得到一条平行于
L
L
L
的直线。

设
L
L
L
是通过
0
\boldsymbol 0
0
与
v
\boldsymbol v
v
的直线,
L
L
L
的每个点加上
p
\boldsymbol p
p
后得到平移后的直线,注意,
p
\boldsymbol p
p
也在平移后的直线上。于是,
A
x
=
b
A\boldsymbol x = \boldsymbol b
A
x
=
b
的解集是一条通过
p
\boldsymbol p
p
而平行于
A
x
=
0
A\boldsymbol x = \boldsymbol 0
A
x
=
0
的解集(
t
v
t\boldsymbol v
t
v
)的直线。
下列定理做了总结:
设方程
Ax
=
0
A\boldsymbol x = \boldsymbol 0
A
x
=
0
对某个
b\boldsymbol b
b
是相容的,
p\boldsymbol p
p
为一个特解,则
Ax
=
b
A\boldsymbol x = \boldsymbol b
A
x
=
b
的解集是所有形如
w=
p
+
v
h
\boldsymbol w =\boldsymbol p + \boldsymbol v_h
w
=
p
+
v
h
的向量的集,其中
vh
\boldsymbol v_h
v
h
是齐次方程
Ax
=
0
A\boldsymbol x = \boldsymbol 0
A
x
=
0
的任意一个解。
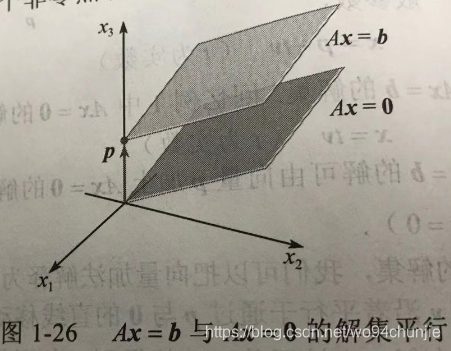
下面描述了
R
3
\mathbb R^3
R
3
中有两个自由变量的情况:
把解集表示成参数向量形式的步骤
- 把增广矩阵行化简为简化阶梯形
- 把每个基本变量用自由变量表示
-
把一般解
x\boldsymbol x
x
表示成向量,如果有自由变量,其元素依赖于自由变量 -
把
x\boldsymbol x
x
分解为向量(元素为常数)的线性组合,用自由变量作为参数