博客

栈的实现：

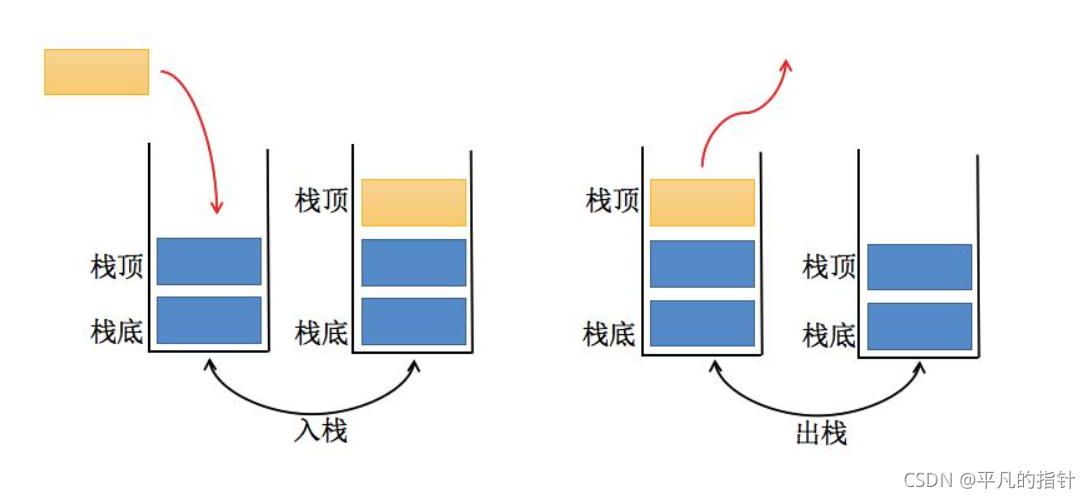
一、栈的概念和性质

栈（stack）又名堆栈，它是一种运算受限的线性表。限定仅在固定的一端进行插入和删除操作的线性表。这一端被称为栈顶，相对地，把另一端称为栈底。栈中的数据元素遵守后进先出LIFO（Last In First Out）的原则。


压栈：

栈的插入操作叫做进栈/压栈/入栈，入数据在栈顶。


出栈：

栈的删除操作叫做出栈。出数据也在栈顶

二、栈的实现思路

栈的实现一般可以使用数组或者链表实现，相对而言数组的结构实现更优一些。因为数组在尾上插入数据的代价比较小这里我们用顺序表结构来实现栈。

顺序表可以把使用的空间写成固定值，也可以构建动态开辟内存；但是如果写成固定的数组形式当存的数据满了就不能再使用了，所以下面我们实现的是动态开辟内存的形式。

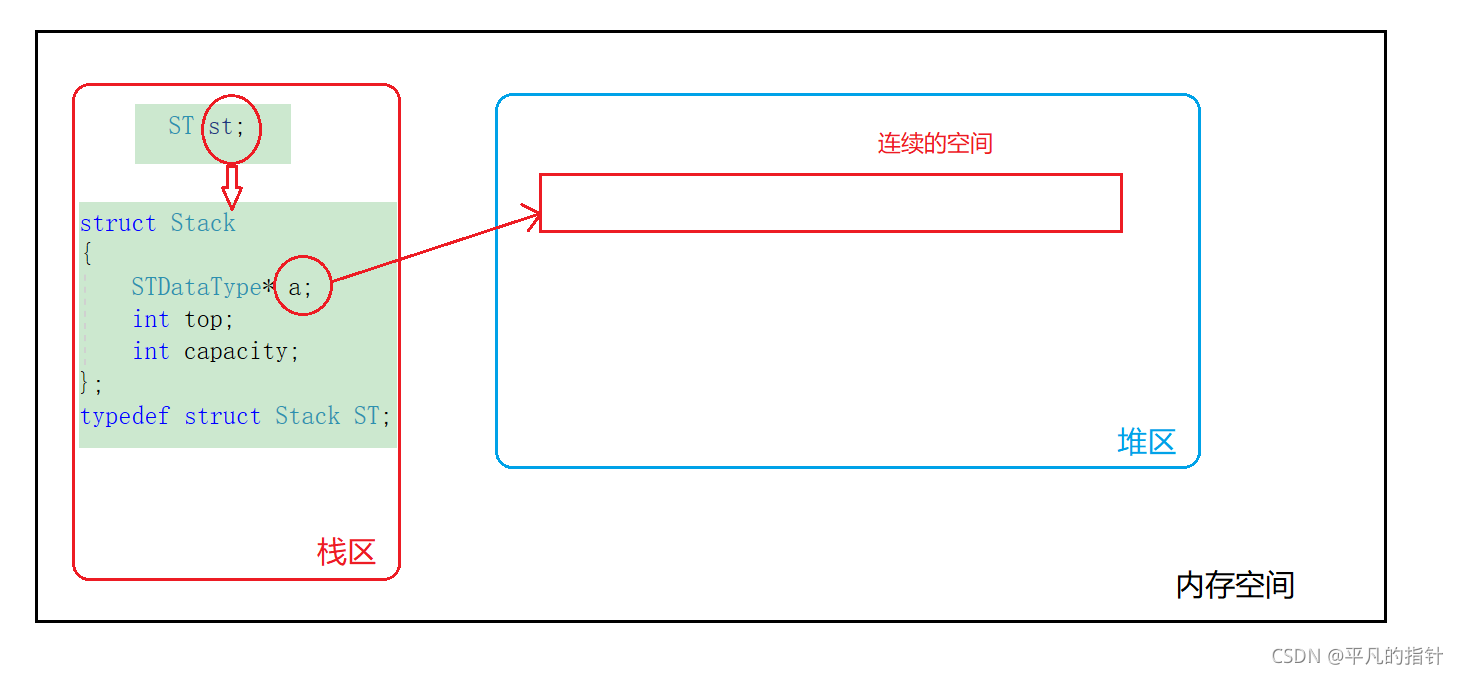
所以我们先创建一个顺序表结构体类型，结构体类型中有指针，下标，容量。


指针：

用来维护在堆上连续的一段空间，


下标：

表示数据存放到哪一个位置了，因为数据只能一个接着一个地存放，要有个下标来记录我数据放到哪一个位置了。


容量：

与下标相比较，当下标与容量相等就表示空间存储满了，要进行扩容处理。

创建类型如下：

typedef int STDataType; //对int类型重新起个名字叫DataType

//创建一个栈结构体类型
struct Stack   
{
	STDataType* a; //数据的指针
	int top;    //栈顶
	int capacity; //记录开辟空间的最大下标处
};

//对顺序表类型struct Stack类型重新起个名字叫SL
typedef struct Stack ST;  

//当size 和 capacity相等时要进行扩容处理

三、栈的相关变量内存布局图

四、栈的初始化和销毁

//初始化变量st
void StackInit(ST* ps)
{
	ps->a = NULL;
	ps->capacity = 0;
	ps->top = 0;
}

//栈的销毁
void StackDestroy(ST* ps)
{
	free(ps->a);
	ps->a = NULL;
	ps->top = 0;
	ps->capacity = 0;
}

五、栈的接口实现：

1.入栈

//入栈
void StackPush(ST* ps, STDataType x)
{
	assert(ps);
	//内存满了要扩容
	if (ps->capacity == ps->top)
	{
		ps->capacity = ps->capacity > 0 ? ps->capacity * 2 : 2;
		STDataType* tmp = 
		(STDataType*)realloc(ps->a,sizeof(STDataType) * ps->capacity);
		if (tmp == NULL)
		{
			perror("erron ");
			exit(-1);
		}
		ps->a = tmp;
	}
	//没有满就直接在后面入栈
	ps->a[ps->top] = x;
	ps->top++;

}

2.出栈

//出栈，要注意栈不能为空
void StackPop(ST* ps)
{
	assert(ps);
	//栈为空就不能再出栈了
	assert(ps->top >= 1);

	ps->top--;
}

3.获取栈顶的数据

//返回栈顶的元素
STDataType StackTop(ST* ps)
{
	assert(ps);
	//栈不能为空
	assert(ps->top >= 1);
	return ps->a[ps->top - 1];

}

4.获取栈的元素个数

//获取栈的元素个数
int StackSize(ST* ps)
{
	assert(ps);
	assert(ps->top >= 1);
	return ps->top - 1;
}

5.判断栈是否为空

//判断栈是否为空
bool StackEmpty(ST* ps)
{
	return ps->top == 0;
}

队列的实现：

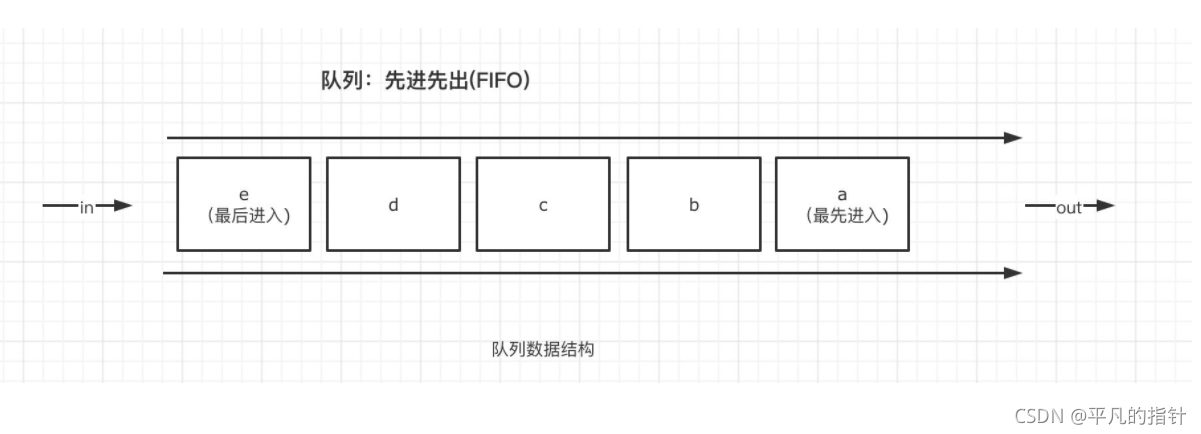
一、队列的概念和性质

队列：

只允许在一端进行插入数据操作，在另一端进行删除数据操作的特殊线性表，队列具有先进先出FIFO(First In First Out)的性质。


队列：

进行插入操作的一端称为队尾


出队列：

进行删除操作的一端称为队头

二、队列的实现思路

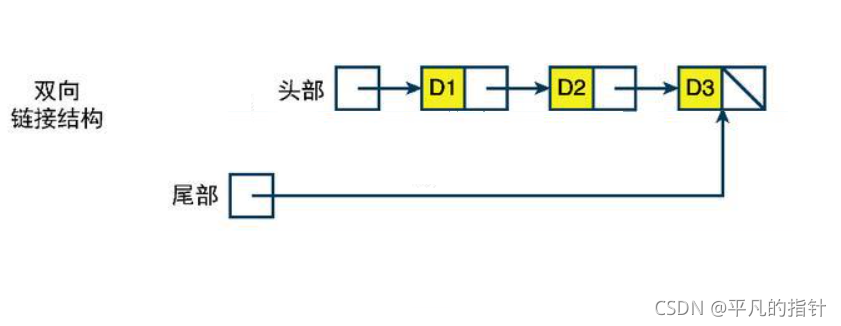
队列也可以数组和链表的结构实现，使用链表的结构实现更优一些，因为如果使用数组的结构，出队列在数组头上出数据，效率会比较低。

而链表我们采用双向链接结构，一个指针来维护头节点，一个指针维护尾部节点

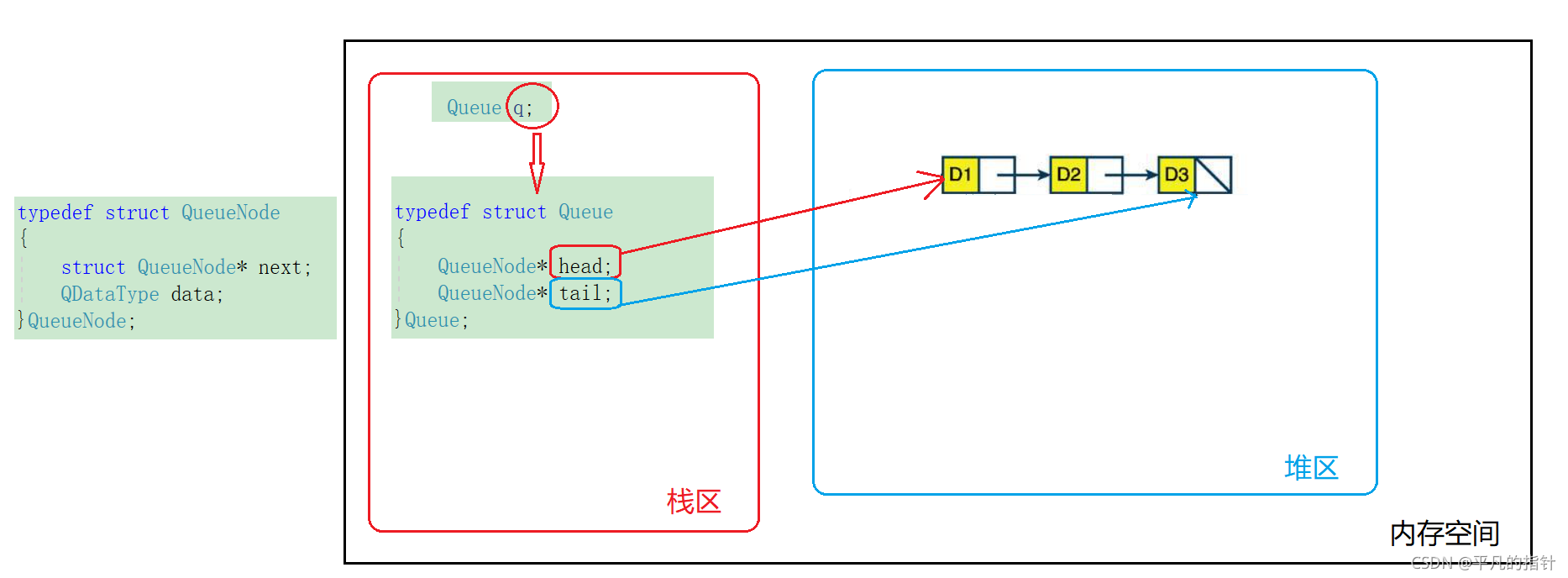
定义的结构体类型如下：

typedef int QDataType;

//创建一个结点型结构体
typedef struct QueueNode
{
	struct QueueNode* next;
	QDataType data;
}QueueNode;

//创建一个队列
typedef struct Queue
{
	QueueNode* head;
	QueueNode* tail;
}Queue;

三、队列相关变量的内存布局图

四、队列的初始化和销毁

//初始化队列
void QueueInit(Queue* pq)
{
	assert(pq);
	pq->head = NULL;
	pq->tail = NULL;
}

//队列销毁
void QueueDestroy(Queue* pq)
{
	assert(pq);
	QueueNode* cur = pq->head;
	while (cur != NULL)
	{
		QueueNode* next = cur->next;
		free(cur);
		cur = next;
	}
	pq->head = NULL;
	pq->tail = NULL;
}

五、队列的接口实现：

1. 入数据

//入数据有两种情况
void QueuePush(Queue* pq,QDataType x)
{
	assert(pq);
	QueueNode* newNode = (QueueNode*)malloc(sizeof(QueueNode));
	if (newNode == NULL)
	{
		perror("erron ");
		exit(-1);
	}
	newNode->next = NULL;
	newNode->data = x;
	//1.入队列时队列为空状态
	if (pq->head == NULL)
	{
		pq->head = newNode;
		pq->tail = newNode;
	}
	//2.入队列，队列不为空，直接在尾指针后面链接即可
	else
	{
		pq->tail->next = newNode;
		pq->tail = newNode;
	}
}

2.出数据

//出数据，类似链表的头删
void QueuePop(Queue* pq)
{
	assert(pq);
	//要保证队列不能为空
	assert(pq->head != NULL);
	QueueNode* next = pq->head->next;
	free(pq->head);
	pq->head = next;

	//防止野指针出现，当队列为空时要把tail指针置为空
	if (pq->head == NULL)
	{
		pq->tail = NULL;
	}
}

3.取队头数据

//取队头数据
QDataType QueueFront(Queue* pq)
{
	assert(pq);
	//检验队列不能为空
	assert(pq->head != NULL);
	return pq->head->data;
}

4.取队尾数据

//取队尾数据
QDataType QueueBack(Queue* pq)
{
	assert(pq);
	//同样要检验队列不能为空
	assert(pq->head != NULL);
	return pq->tail->data;
}

5.获取队列元素个数

//获取队列元素个数
int QueueSize(Queue* pq)
{
	assert(pq);
	int count = 0;
	QueueNode* cur = pq->head;
	while (cur != NULL)
	{
		count++;
		cur = cur->next;
	}
	return count;
}

6.判断队列是否为空

//判断队列是否为空
bool QueueEmpty(Queue* pq)
{
	return pq->head == NULL;
}

总结

以上就是栈和队列的实现内容了，其中前面我只有把源文件Stack.c 和Queue.c拆开来分析了。如果想要栈和队列的全部内容，阔以移步到gitee上获取


【栈的源码链接，点击即可】



【队列的源码链接，点击即可】