在本实验中,主要学习了多变量函数的定义以及图像绘制。
通过对范德瓦尔斯方程做恒等变换,将
(
p
+
a
V
2
)
(
V
−
b
)
=
R
T
(p+\frac{a}{V^2})(V-b)=RT
(
p
+
V
2
a
)
(
V
−
b
)
=
R
T
化为
p
=
R
T
V
−
b
−
a
V
2
p=\frac{RT}{V-b}-\frac{a}{V^2}
p
=
V
−
b
R
T
−
V
2
a
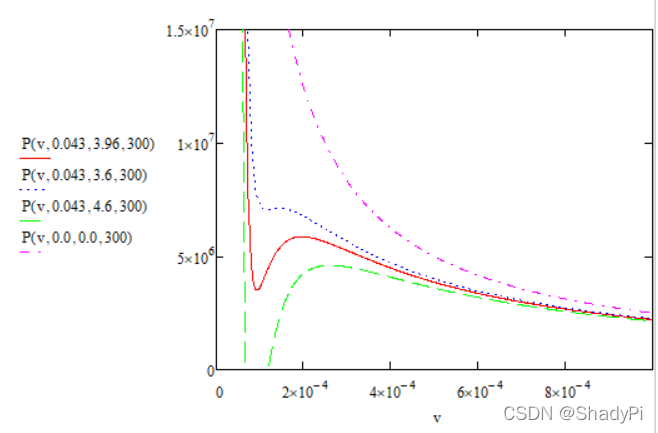
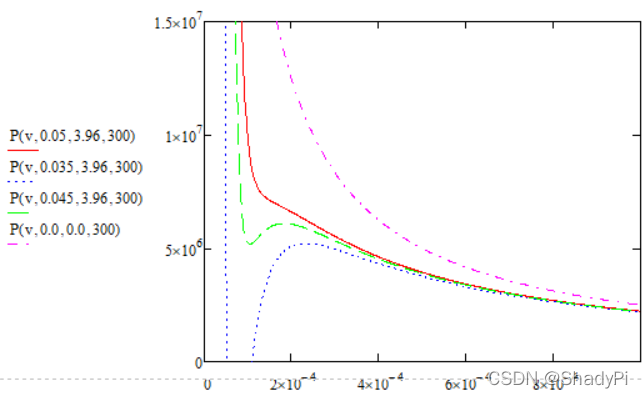
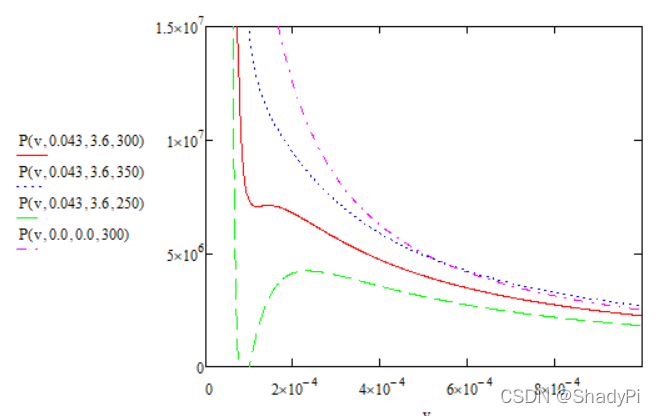
此时,p为关于a,b,V,T四个变量的常数,我们可以通过控制变量的方法,绘制多幅p-V图,从而观察范德瓦尔斯方程中的若干参数对气体特性的影响。
定义函数P(v,b,a,T)如下:
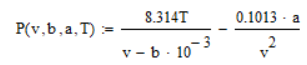
可得下面三幅p-V图像,变量分别为a,b和T: