本文涉及到信号处理的基本知识,主要为图像处理与模式识别打基础。
信号的定义
定义及数学表示
-
信号是一种随时间或空间变化的物理现象或物理量
– 如声音、图像、视频等 -
信号的表示:
– 可以由一个或多个独立变量构成的函数来表示 -
一维声音信号
A(
t
)
A(t)
A
(
t
)
、二维图像信号
I(
x
,
y
)
I(x,y)
I
(
x
,
y
)
、三维视频
信号
V(
x
,
y
,
t
)
V(x,y,t)
V
(
x
,
y
,
t
)
– 绘出函数的图像称为信号的波形
– 各种变换、频谱分析等
分类
-
信号在不同的规则下具有不同的分类方式
– 确定性信号与随机信号
– 奇信号与偶信号
– 一维信号和多维信号
– 连续时间信号和离散时间信号
– 周期信号和非周期信号
– 模拟信号和数字信号
具体分类依据不再展开,可参考其他网络资料
信号的基本运算
这些了解即可
-
移位(时移或延时)
F(
t
)
=
f
(
t
−
t
0
)
F(t) =f(t-t_0)
F
(
t
)
=
f
(
t
−
t
0
)
-
反转变换(反褶)
F(
t
)
=
f
(
−
t
)
F(t) =f(-t)
F
(
t
)
=
f
(
−
t
)
-
尺度变换(压缩与扩展)
F(
t
)
=
f
(
a
t
)
F(t) =f(at)
F
(
t
)
=
f
(
a
t
)
-
微分与积分
F(
t
)
=
f
′
(
t
)
=
d
d
t
f
(
t
)
F
(
t
)
=
∫
−
∞
t
f
(
τ
)
d
τ
F(t) =f'(t) = \frac{d}{dt}f(t) \\ F(t) = \int_{-\infty}^{t}f(\tau)d\tau
F
(
t
)
=
f
′
(
t
)
=
d
t
d
f
(
t
)
F
(
t
)
=
∫
−
∞
t
f
(
τ
)
d
τ
-
加法与乘法
F(
t
)
=
f
1
(
t
)
+
f
2
(
t
)
F
(
t
)
=
f
1
(
t
)
∗
f
2
(
t
)
F(t) = f_1(t)+f_2(t) \\ F(t) = f_1(t)*f_2(t)
F
(
t
)
=
f
1
(
t
)
+
f
2
(
t
)
F
(
t
)
=
f
1
(
t
)
∗
f
2
(
t
)
- 基本信号分解。下面将具体介绍。
信号的分解
-
为了便于研究信号的传输和处理问题,往往将信
号分解为一些简单(基本)的信号之和 -
分解角度不同,可以分解为不同的分量
– 直流与交流分解:直流分量与交流分量
– 奇偶分解:偶分量与奇分量
– 虚数的虚实分解:实部分量与虚部分量
– 脉冲分解:脉冲分量
– 正交分解:正交函数分量
信号的脉冲分解
脉冲函数
脉冲函数也称
δ
\delta
δ
函数。若在一维空间中,自变量为时间
t
t
t
的函数,满足下述两个条件:
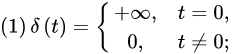
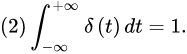
把满足上述两个条件的函数称为函数
δ
\delta
δ
,记作
δ
(
t
)
\delta(t)
δ
(
t
)
。
δ
\delta
δ
函数是一种广义函数,也可以扩展到多维空间中,它的确切意义应该在积分运算下理解:其积分曲线高度为“无限高”,而宽度为“无限窄”,曲线下的面积等于1。因此,
δ
\delta
δ
函数有下述关系式
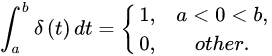
脉冲函数的性质
性质一:偶函数
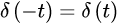
显而易见,不做赘述
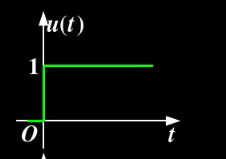
性质二:积分得到阶跃函数
设
u
(
t
)
u(t)
u
(
t
)
为单位阶跃函数,即
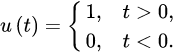
则有
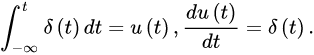
脉冲函数与阶跃函数都具有比较好的性质,接下来通过阶跃函数,推导出性质三:筛选性质。
性质三:筛选性质
矩形脉冲
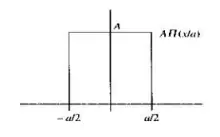
将一个信号用矩形脉冲来逼近

当
t
=
τ
t=\tau
t
=
τ
时,脉冲高度为
f
(
τ
)
f(\tau)
f
(
τ
)
,脉宽为
Δ
τ
\Delta\tau
Δ
τ
,则此窄脉冲可表示为
f
(
τ
)
[
u
(
t
−
τ
)
−
u
(
t
−
τ
−
Δ
τ
)
]
f(\tau)[u(t-\tau) – u(t-\tau – \Delta\tau)]
f
(
τ
)
[
u
(
t
−
τ
)
−
u
(
t
−
τ
−
Δ
τ
)
]
.
这个窄脉冲(矩形脉冲)可以好好体会一下。
得到了一个窄脉冲基于阶跃函数的表示,那么整个信号的表示只需要对
τ
\tau
τ
求和。

至此,我们回到了用
δ
\delta
δ
表示一个信号,得到公式
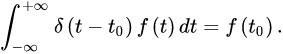
这就是
筛选性质
,同时,原信号被分解,这就是
脉冲分解
。
信号的正交分解
- 如果用正交函数集来表示一个信号,那么,组成信号的各分量就是相互正交的
- 正交分解是傅里叶变换、余弦变换等的基础
后续会更新本节内容并上链接