博客

前面的文章中介绍到单链表，它的尾结点（最后一个结点）的指针域next都是指向null，如下图：



单链表的指针域只存储了向后的指针，到了尾结点就无法继续向后的操作。

本篇文章将介绍单向循环链表，它和单链表的区别在于结尾点的指针域不是指向null，而是指向头结点，形成首尾相连的环。这种首尾相连的单链表称为

单向循环链表

。循环链表可以从任意一个结点出发，访问到链表中的全部结点。

和单链表一样，为了使空链表与非空链表处理一致，我们通常会设置一个头结点。当然，之前提到的单链表和本文的单向循环链表都不是必须要有头结点，只是为了简化操作。

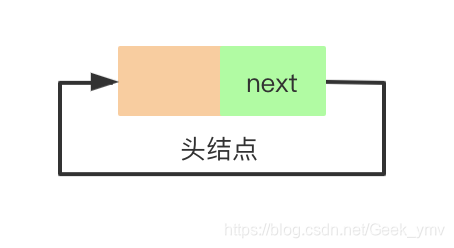
单向循环链表的查找、删除和修改操作与单链表一致（这里不在赘述，可参考前面的文章），插入操作和单链表有所不同，单向循环链表需要维持环状结构。判断单链表为空的条件是head.next == null，而判断单向循环链表为空的条件为head.next == head。如下图所示，单向循环链表初始化时，头结点的next域指向自身，形成环状结构。

public SingleCycleLinkedList() {
    head = new Node();
    // 初始化时头结点的next域指向自身，形成环
    head.next = head;
}

比如现在要在尾部插入结点a，如下：



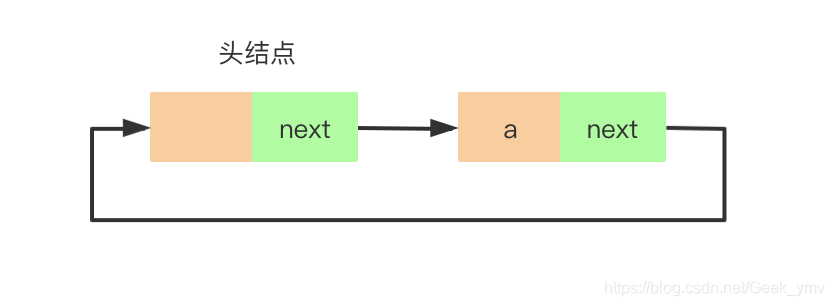
首先遍历链表找到尾结点，那么如何找到这个尾结点呢，我们知道单向循环链表中尾结点的next域指向头结点，所以当

tmp.next == head

的时候tmp指向的就是尾结点。

// 找到尾结点
Node tmp = head;
while (tmp.next != head) {
    tmp = tmp.next;
}

插入操作的完整代码如下，仅供参考

public class SingleCycleLinkedList {

    // 头结点
    private Node head;

    public SingleCycleLinkedList() {
        head = new Node();
        // 初始化时头结点的next指向自身
        head.next = head;
    }

    public boolean add(Integer item) {
        // 新创建一个结点
        Node newNode = new Node(item, null);

        // 找到尾结点
        Node tmp = head;
        while (tmp.next != head) {
            tmp = tmp.next;
        }

        // 这个时候tmp指向尾结点（即tmp.next = head），新结点的next指向head。
        newNode.next = tmp.next;
        tmp.next = newNode;

        return true;
    }

    public void list() {
        Node tmp = head;
        while (tmp.next != head) {
            tmp = tmp.next;
            System.out.println(tmp.item);
        }
    }

    private static class Node {

        private Integer item;

        private Node next;

        public Node() {
        }

        public Node(Integer item, Node next) {
            this.item = item;
            this.next = next;
        }
    }
}

上述代码的插入操作，为了找到尾结点每次都要从头开始遍历链表，效率很低。我们可以定义一个尾指针指向链表的尾结点来进行优化，这样每次插入操作的时间复杂度就变成了O(1)。

在下一篇文章中，我会使用单向循环链表解决约瑟夫问题，其中就会用到尾指针，敬请期待。

参考文章

• 单链表为什么要设置头结点 https://www.cnblogs.com/youxin/p/3279391.html
• 单向循环链表 https://www.cnblogs.com/ssyfj/p/9424850.html

「更多精彩内容请关注公众号geekymv，喜欢请分享给更多的朋友哦」