机器学习/深度学习几种典型学习范式|主动学习
主动学习(Active Learning,AL):
原论文详细介绍
Active Learning Literature Surve
Introduction
主动学习背后的关键思想是,如果允许机器学习算法选择要学习的数据,那么它可以用更少的标记训练实例实现更高的准确性。也就是说主动学习的应用场景是数据量大二标签少的场景,动机是减少人工标注的成本,提高学习的效率。一个积极的学习者可能会以未标记的实例的形式提出问题,比如在我们中学时代或者日常的学习过程中,总有一些理解不到位学不透的地方,所以我们会针对这些我们还没有搞懂的知识主动积极的向老师和同学寻求帮助,已达到解惑的目的,主动的学习的思想就与这个过程相似。在许多现代机器学习问题中,主动学习具有良好的动机,在这些问题中,未标记数据可能很丰富,但标签很难获得、耗时或昂贵。
主动学习(也被称为“查询学习”,在统计学文献中有时被称为“最佳实验设计”)是机器学习的一个子领域,更普遍地说,是人工智能的一个子领域。关键的假设是,如果允许学习算法选择它学习的数据——如果你愿意的话,可以让它“好奇”——它将在较少的训练下表现得更好。
主动学习的例子
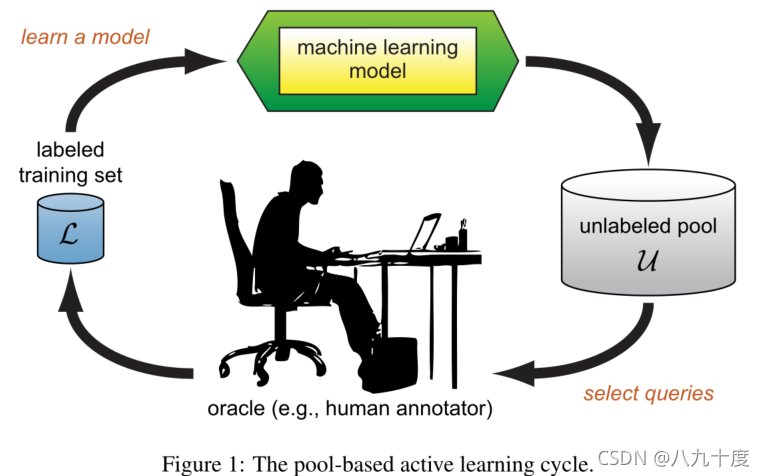

主动学习又叫查询学习,顾名思义,有一些不同的查询策略用于决定哪些实例提供的信息最多。以上都是两种pool-based的主动学习实例,选用的查询策略为不确定抽样查询策略(选择池中模型最不确定如何标记的实例)。
【图1】展示了基于池的主动学习循环。学习者可以从有标签的训练数据集
L
\mathcal{L}
L
中开始,为一个或者多个精心选择的实例查询标签,从查询结果中学习,然后利用它的新知识选择下一个要查询的实例。一旦进行了查询,学习算法部分通常就没有额外的假设了。新的有标签的实例被简单地添加至有标签的数据集
L
\mathcal{L}
L
中,学习者一标准的监督学习方式继续学习。但也有一些例外情况,比如允许学习者进行其他类型的查询,或者当主动学习与半监督学习相结合时。
【图2】展示了以一种容易想象的方式进行主动学习的潜力。这是一个玩具数据集,由两个以(-2,0)和(2,0)为中心的高斯函数生成,标准差σ=1,每个代表一个不同的类分布。图2(a)显示了抽样400个实例(每个类200个)后的结果数据集;实例被表示为二维特征空间中的点。在现实环境中,这些实例可能是可用的,但它们的标签通常是不可用的。图2(b)显示了传统的监督学习方法,在随机选择30个实例进行标记后,从未标记的池中抽取
U
\mathcal{U}
U
。这条线显示了使用这30个点训练的logistic回归模型(即后验值等于0.5)的线性决策边界。注意,在这个训练集中,大多数已标记的实例在水平轴上都远不是零,就是贝叶斯最优决策边界的位置。因此,该分类器在剩余未标记点上只能达到精度=0.7。然而,图2©讲述了一个非常不同的故事。主动学习者使用不确定性采样来关注最接近其决策边界的实例,假设它能充分解释以u为特征的输入空间的其他部分。因此,它避免了为冗余或不相关的实例请求标签,并且仅用30个已标记实例就实现了精度=0.9。与“被动”监督学习(即随机抽样)相比,这减少了67%的错误,而且只有不到10%的数据被标记。
应用场景

学习者提出查询的场景有很多种,这里主要讲3种:
- 成员查询合成;
- 流式选择抽样;
- 基于池的主动学习。
成员查询合成
在这种设置下,学习者可以为输入空间中任何未标记的实例请求标签,包括(通常是假设)学习者重新生成的查询,而不是从某些潜在的自然分布中采样的查询。对于有限的问题域,高效的查询合成通常是易于处理和高效的。综合查询的思想也被扩展到回归学习任务中,例如学习预测机器人手的绝对坐标,给定其机械臂的关节角度作为输入。
(这一块的英文原作没有理解透,也没有十分清楚到底什么是成员查询合成)
流式选择抽样
综合查询的另一种选择是选择性抽样。关键的假设是获得一个未标记的实例是免费的(或廉价的),所以它可以首先从实际分布中取样,然后学习者可以决定是否请求它的标签。这种方法被称作流式主动学习或者顺序主动学习(stream-basedorsequentialactive learning),因为每个未标记的实例通常一次从数据源中提取一个,学习者必须决定是查询还是丢弃它。如果输入分布是均匀的,选择抽样可以很好地表现为成员查询学习。然而,如果分布是非均匀的(更重要的是)未知的,我们可以保证查询仍然是合理的,因为它们来自真实的底层分布。
决定是否查询一个实例的方式:
- 使用一些“信息量测量”或者“查询策略”来评估样本,信息量越多的样本就越有可能被查询;
- 计算一个显示的不确定区域,即实例空间中对学习者来说仍然不明确的部分,并且只查询属于它的实例。一个朴素的方法是为定义该区域的信息度量设置一个最低门槛。然后查询评估值高于此阈值的实例。另一种更有原则的方法是定义整个模型类仍然未知的区域,即与当前标记的训练集一致的假设集,称为版本空间(version space)。换句话说,如果同一模型类的任意两个模型(但不同的参数设置)有一致的标签,但是在一些未标注的实例上存在分歧,那么该实例就属于不确定范围。但是,完全且显式地计算这个区域的计算开销很大,并且在每次新的查询之后都必须维护它。因此,在实践中使用近似法。
基于池的主动学习
对于许多现实世界中的学习问题,可以一次性收集大量未标记的数据。基于这种动机,基于池的主动学习,假设有一小组标记数据和大量的未标记数据可用。查询是有选择地从池中提取的,池通常被假定为关闭的(即静态的或不变的),尽管这并不是严格必需的。通常,根据用于评估池中所有实例(或者,如果
U\mathcal{U}
U
非常大,则可能是其中的一些子样本)的信息性度量,以一种贪婪的方式查询实例。
基于池的场景已经在现实应用中被广泛研究,如:文本分类、信息提取、图像分类与检索、视频分类与检索、语音识别、癌症诊断等等。
基于流的主动学习和基于池的主动学习的主要区别在于前者顺序地扫描数据并单独做出查询决定,而后者在选择最佳查询之前对整个集合进行评估和排名。虽然基于池的场景似乎在应用程序论文中更常见,但可以想象,在哪些设置中基于流的方法更合适。例如,当内存或处理能力可能受到限制时,如移动和嵌入式设备。
查询策略框架
所有的主动学习场景都需要评估未标记实例的信息量,这些实例既可以从头生成,也可以从给定的分布中取样。在文献中已经提出了许多构建此类查询策略的方法。
以下
xA
∗
x_A^{\ast}
x
A
∗
表示某些查询选择算法
AA
A
中的信息量最丰富的实例。
不确定性抽样Uncertainty Sampling
不确定性抽样也许是最简单最常用的查询框架。在这个框架中,主动学习者会查询最不确定如何标注的实例。对于概率学习模型来说,这种方法通常是直接的。例如,当使用概率模型进行二元分类时,不确定性抽样策略简单地查询后验概率为正的最接近0.5的实例
更一般的不确定性抽样策略使用熵作为不确定性度量:
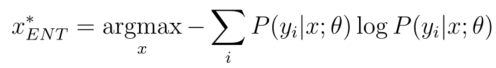
y
i
y_i
y
i
涵盖了所有可能的标签。信息理论中的熵,表示“编码”一个分布所需的信息量。因此,它通常被认为是机器学习中不确定性或杂质的衡量标准。对于二分类问题,基于熵的不确定抽样与选择后验最接近0.5的实例相同。然而,基于熵的方法可以很容易地推广到更复杂的结构化实例的概率多标签分类器和概率模型,如序列和树。在这些更复杂的设置中,熵的替代方法包括查询最佳标记最小置信度的实例:
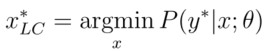
其中,
y
∗
=
a
r
g
m
a
x
y
P
(
y
∣
x
;
θ
)
y^{\ast} = argmax_yP(y|x;\theta)
y
∗
=
a
r
g
m
a
x
y
P
(
y
∣
x
;
θ
)
是最可能的类标记。
不确定性抽样策略也可用于非概率模型。探索不确定性采样的第一个工作是使用决策树分类器,修改它以具有概率输出。类似的方法也被用于最近邻(也就是“基于记忆的”或“基于实例的”)分类器的主动学习,允许每个邻居对x的类标签进行投票,这些投票的比例代表后验标签概率。Tong和Koller(2000)还试验了支持向量机或支持向量机的不确定性采样策略(Cortes和V apnik,1995),其中涉及查询最接近线性决策边界的实例。最后一种方法类似于使用概率二元线性分类器的不确定性采样,如逻辑回归或朴素贝叶斯。
基于委员会的查询Query-By-Committee
QBC方法包括维持一个委员会
C
=
θ
(
1
)
,
.
.
.
,
θ
(
C
)
\mathcal{C}={\theta^{(1)},…,\theta^{(C)}}
C
=
θ
(
1
)
,
.
.
.
,
θ
(
C
)
,这些模型都是在当前标记的数据集
L
\mathcal{L}
L
上训练的,但代表了相互竞争的假设。然后,每个委员会成员都被允许对提问候选人的标签进行投票。最有信息量的问题被认为是他们最不同意的问题。
QBC框架背后的基本前提是最小化版本空间,这是(如2.2节所述)与当前标记的训练数据
L
\mathcal{L}
L
一致的一组假设。

【图5】给出了(a)线性函数和(b)轴平行箱式分类器在不同的二元分类任务中的版本空间概念。如果我们将机器学习视为在版本空间中搜索“最佳”模型,那么主动学习的目标就是尽可能地限制这个空间的大小(以便搜索能够更精确),使用尽可能少的标记实例。这正是QBC所做的,通过查询输入空间中有争议的区域。为了实现QBC选择算法,必须:
- 能够构建一个代表版本空间不同区域的模型委员会,并且
- 委员会成员之间存在一定程度的分歧。
为了测量分歧的程度,提出了两种主要的方法。第一个是投票熵:
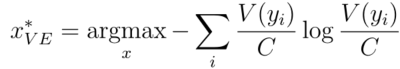
其中,
y
i
y_i
y
i
也涵盖了所有可能的标签。
V
(
y
i
)
V(y_i)
V
(
y
i
)
是一个标签从委员会成员的预测中获得的“票数”。这可以被认为是基于熵的不确定性抽样的QBC推广。另一个被提出的分歧度量是平均分歧(KL) (平均KL散度):
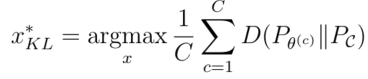
其中:
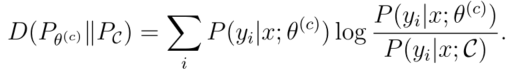
θ
(
c
)
\theta^{(c)}
θ
(
c
)
表示委员会中的一个特定模型,
C
\mathcal{C}
C
表示整体委员会。因此:
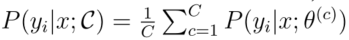
是
y
i
y_i
y
i
是正确标签的“共识”概率。KL散度是两种概率分布差异的信息理论度量。因此,这个分歧衡量标准认为,任何一个委员会成员的标签分布与共识之间的平均差异最大的问题,信息最丰富。
基于模型变化期望的查询
另一个通用的主动学习框架是查询实例,如果我们知道它的标签,它将给当前模型带来最大的变化。该框架中的一个查询策略示例是用于鉴别概率模型类的“期望梯度长度”(EGL)方法。该策略由赛德斯等人引入,用于多实例环境下的主动学习(见第5.4节),并已应用于CRFs等概率序列模型。
由于判别概率模型通常使用基于梯度的优化来训练,因此模型的“变化”可以通过训练梯度的长度(即用于重新估计参数值的向量)来衡量。换而言之,学习者应该查询的情况是:如果实例被标记或者加入
L
\mathcal{L}
L
,将会新的最大幅度幅度的训练梯度。
假设
∇
l
(
L
;
θ
)
\nabla{\mathcal{l}(\mathcal{L};\theta)}
∇
l
(
L
;
θ
)
是目标函数
l
\mathcal{l}
l
的梯度,
θ
\theta
θ
为模型参数。现在让
∇
l
(
L
⋃
⟨
x
,
y
⟩
;
θ
)
\nabla{\mathcal{l}(\mathcal{L}\bigcup \langle{x,y}\rangle;\theta)}
∇
l
(
L
⋃
⟨
x
,
y
⟩
;
θ
)
作为
L
\mathcal{L}
L
加上训练元组
⟨
x
,
y
⟩
\langle{x,y}\rangle
⟨
x
,
y
⟩
得到的新的梯度。由于查询算法事先不知道真正的标签,我们必须计算长度作为对可能标签的期望:
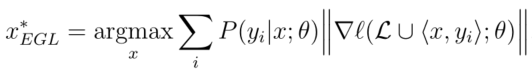
其中
∥
⋅
∥
\Vert {\cdot} \Vert
∥
⋅
∥
每个梯度向量的欧几里得范数。注意,对于查询时间,
∥
∇
l
(
L
;
θ
)
∥
\Vert {\nabla{\mathcal{l}(\mathcal{L};\theta)}} \Vert
∥
∇
l
(
L
;
θ
)
∥
应该是接近于0的,因为
l
\mathcal{l}
l
在上一轮训练中是收敛的。因此,可以近似:
∇
l
(
L
⋃
⟨
x
,
y
⟩
;
θ
)
≈
∇
l
(
⟨
x
,
y
⟩
;
θ
)
\nabla{\mathcal{l}(\mathcal{L}\bigcup \langle{x,y}\rangle;\theta)} \approx \nabla{\mathcal{l}(\langle{x,y}\rangle;\theta)}
∇
l
(
L
⋃
⟨
x
,
y
⟩
;
θ
)
≈
∇
l
(
⟨
x
,
y
⟩
;
θ
)
考虑到计算效率,因为假设训练实例是独立的。
这个框架背后的直觉是,它更喜欢那些可能对模型影响最大的实例(即对其参数影响最大的实例),而不管结果是什么查询标签。这种方法已经在实证研究中被证明工作得很好,但是如果特征空间和标签集都非常大,就会在计算上非常昂贵。’’
基于方差减少的查询(Variance Reduction and Fisher Information Ratio)
- 通过最小化未来方差确定;
-
使Fisher信息比率最小化,
缺点是计算复杂度较高。
估计误差减少
估计误差减少框架具有接近最优和不依赖于模型类的双重优势。但是计算效率非常昂贵,所以常常使用增量学习或者近似技术。
基于密度权重的选择方法
有人指出,不确定性抽样和QBC策略容易查询离群点,这是Fisher信息和估计误差减少框架背后的主要激励因素。【图6】说明了使用不确定抽样的二元线性分类器的这个问题。最不确定的实例位于分类边界,但不是分布中其他实例的“代表性”,因此知道它的标签不太可能提高数据的整体准确性。QBC和EGL可能会表现出类似的行为,通过花费时间查询可能的离群值,仅仅是因为它们有争议,或者期望在模型中进行重大更改。Fisher信息和估计误差减少策略通过在估计比率和未来误差时使用未标记池
U
\mathcal{U}
U
(分别)隐式地避免了这些陷阱。我们还可以对查询选择策略中的输入分布进行显式建模。

settle和Craven(2008)提出的信息密度框架是一种密度加权技术,在settle(2008)的第4章中进行了进一步分析。其主要思想是,信息性实例不仅应该是那些不确定的实例,还应该是那些“代表”输入分布的实例(即位于输入空间的密集区域)。因此,我们希望以如下方式查询实例:
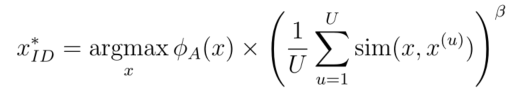
其中,
ϕ
A
(
x
)
\phi_{A}(x)
ϕ
A
(
x
)
某个不确定性采样方法或者QBC,表示
x
x
x
的信息量。
β
\beta
β
表示是控制密度项相对重要性的指数参数。
Settles和Craven(2008)表明,如果密度可以有效地预先计算并缓存以备用,则选择下一个查询所需的时间基本上与基本信息度量(例如,不确定性采样)没有什么不同。
主动学习的分析
本节讨论了主动学习在实践中如何以及何时起作用的一些经验和理论证据。
主动学习的相关研究领域
主动学习的研究是由两个关键思想驱动的:(i)学习者应该被允许提出问题,(ii)未标记的数据经常是现成的或很容易获得的。也有一些相关的研究领域,有丰富的文献。
- 半监督学习Semi-Supervised Learning
- 强化学习Reinforcement Learning
- 等价查询学习Equivalence Query Learning
- 主动类选择Equivalence Query Learning
- 主动特征获取与分类Active Feature Acquisition and Classification
- Model Parroting and Compression