35、二叉排序树的添加和删除节点

思路：

二叉排序树的定义：形如图1所示，每棵二叉树有一个根节点，根节点下面至多有两个子节点，每个节点只能最多有两个分支节点，并且左侧分支子节点数值小于父节点数值，右侧子节点数值大于父节点数值。

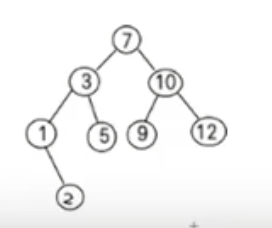
图一

下面介绍了二叉排序树

的增加节点、删除节点（重点）、遍历

。

增加节点

增加节点比较简单，直接上代码（如果增加的节点比当前节点值大，则遍历右侧子树，否则遍历左侧子树，直到遇到节点为空的时候，添加节点）

//添加节点
public void add(Node node) {
	if(node == null) {
		return;
	}
	if(node.getData() > this.getData()) {
		if(this.getRightNode() == null) {
			this.setRightNode(node);
		}else {
			this.getRightNode().add(node);
		}		
	}else {
		if(this.getLeftNode() == null) {
			this.setLeftNode(node);
		}else {
			this.getLeftNode().add(node);
		}
	}	
}

删除节点

分为三种情况：

删除的节点是叶子节点最简单，直接找到父节点，让父节点的子树指向null即可；

删除的节点有一个子节点，也好办，直接让父节点指向删除节点的子节点即可；

删除节点有两个子节点，需要获得右子树节点中的最小值，用来填充删除的位置（原理自己想下，应该好理解），然后删除节点即可。

代码如图

//查找要删除的结点
public Node search(int value) {
	if(rootNode == null) {
		return null;
	} else {
		return rootNode.getDelNode(value);
	}
}

//查找父结点
public Node searchParent(int value) {
	if(rootNode == null) {
		return null;
	} else {
		return rootNode.getDelParNode(value);
	}
}

//找到节点A及以下树的最小节点，并删除它

public int delMin(Node node) {
	Node tempNode = node;
	while(tempNode.getLeftNode() != null) {
		tempNode = node.getLeftNode();	
	}
	del(tempNode.getData());
	return tempNode.getData();
}


//删除节点
public void del(int value) {
	if(rootNode == null) {
		System.out.println("没有root节点！删除失败！");
		return;
	}else {
		//需要找到待删除的节点
		Node delNode = search(value);
		if(delNode == null) {
			return;
		}
		//如果我们发现当前这颗二叉排序树只有一个结点
		if(rootNode.getLeftNode() == null && rootNode.getRightNode() == null) {
			rootNode = null;
			System.out.println("只有一个结点！删除失败！");
			return;
		}
		//去找到targetNode的父结点
		Node parent = searchParent(value);
		
		//1、待删除的节点是叶子节点
		if(delNode.getLeftNode() == null && delNode.getRightNode() == null) {
			if(parent.getLeftNode() != null && parent.getLeftNode().getData() == value) {
				parent.setLeftNode(null);
			}else {
				parent.setRightNode(null);
			}
			System.out.println("value:"+value+"是叶子节点，已经删除！");
		}else if(delNode.getLeftNode() != null && delNode.getLeftNode() != null){
			//2、待删除的节点是叶子节点:她有两个子节点,找到右子树最小的节点填删除的节点		
			delNode.setData(delMin(delNode.getRightNode()));
			System.out.println("value:"+value+"有两个子节点，已经删除！");
		}else {
			//3、待删除的节点不是叶子节点：它有一个子节点
			//如果删除的节点只有左子节点
			//如果要删除的结点有左子结点 
			if(delNode.getLeftNode() != null) {
				if(parent != null) {
					if(parent.getLeftNode().getData() == value) {
						parent.setLeftNode(delNode.getLeftNode());
					}else {
						parent.setRightNode(delNode.getLeftNode());
					}
				}else {
					rootNode = delNode.getLeftNode();
				}
				
			}else{
				if(parent != null) {
					if(parent.getLeftNode().getData() == value) {
						parent.setLeftNode(delNode.getRightNode());
					}else {
						parent.setRightNode(delNode.getRightNode());
					}
				}else {
					rootNode = delNode.getRightNode();
				}
			}
			System.out.println("value:"+value+"有一个子节点，已经删除！");
		}
		
		
			
		
		
		
		
		
		
		
		
	}
	
	
}

遍历节点：中序遍历

//中序遍历
public void infixOrder() {
	if(this.getLeftNode() !=null) {
		this.getLeftNode().infixOrder();
	}
	System.out.println(this.getData());
	if(this.getRightNode() !=null) {
		this.getRightNode().infixOrder();
	}	
}

全部代码：

package binarysorttree;

public class BinarySortTreeDemo {

	public static void main(String[] args) {
		// TODO Auto-generated method stub

		int[] arr = {7, 3, 10, 12, 5, 1, 9, 2};
//		BinarySortTreeDemo binarySortTreeDemo = new BinarySortTreeDemo();
		BinarySortTree binarySortTree = new BinarySortTree(null);
		for (int i = 0; i < arr.length; i++) {
			binarySortTree.add(new Node(arr[i]));
		}
		//中序遍历
		binarySortTree.infixOrder(); 1, 3, 5, 7, 9, 10, 12
		
		
		Node parent = binarySortTree.searchParent(2);
		System.out.println(parent.toString());
//		System.out.println(parent.getLeftNode().getData());
//		parent.getLeftNode().getData()
//		//删除节点
//		binarySortTree.del(2);
		//删除节点
//		binarySortTree.del(1);
		//删除节点
		binarySortTree.del(3);
//		//中序遍历
		binarySortTree.infixOrder(); 1, 3, 5, 7, 9, 10, 12
		
	}

}
//二叉树类
class BinarySortTree{
	private Node rootNode;

	public Node getRootNode() {
		return rootNode;
	}

	public void setRootNode(Node rootNode) {
		this.rootNode = rootNode;
	}

	public BinarySortTree(Node rootNode) {
		super();
		this.rootNode = rootNode;
	}
	
	//添加节点
	public void add(Node node) {
		if(this.rootNode == null) {
			this.rootNode = node;
			return;
		}
		this.rootNode.add(node);
	}
	
	//中序遍历
	public void infixOrder() {
		if(this.rootNode == null) {
			return;
		}
		this.rootNode.infixOrder();
	}
	
	//查找要删除的结点
	public Node search(int value) {
		if(rootNode == null) {
			return null;
		} else {
			return rootNode.getDelNode(value);
		}
	}
	
	//查找父结点
	public Node searchParent(int value) {
		if(rootNode == null) {
			return null;
		} else {
			return rootNode.getDelParNode(value);
		}
	}
	
	//找到节点A及以下树的最小节点，并删除它
	
	public int delMin(Node node) {
		Node tempNode = node;
		while(tempNode.getLeftNode() != null) {
			tempNode = node.getLeftNode();	
		}
		del(tempNode.getData());
		return tempNode.getData();
	}
	
	
	//删除节点
	public void del(int value) {
		if(rootNode == null) {
			System.out.println("没有root节点！删除失败！");
			return;
		}else {
			//需要找到待删除的节点
			Node delNode = search(value);
			if(delNode == null) {
				return;
			}
			//如果我们发现当前这颗二叉排序树只有一个结点
			if(rootNode.getLeftNode() == null && rootNode.getRightNode() == null) {
				rootNode = null;
				System.out.println("只有一个结点！删除失败！");
				return;
			}
			//去找到targetNode的父结点
			Node parent = searchParent(value);
			
			//1、待删除的节点是叶子节点
			if(delNode.getLeftNode() == null && delNode.getRightNode() == null) {
				if(parent.getLeftNode() != null && parent.getLeftNode().getData() == value) {
					parent.setLeftNode(null);
				}else {
					parent.setRightNode(null);
				}
				System.out.println("value:"+value+"是叶子节点，已经删除！");
			}else if(delNode.getLeftNode() != null && delNode.getLeftNode() != null){
				//2、待删除的节点是叶子节点:她有两个子节点,找到右子树最小的节点填删除的节点		
				delNode.setData(delMin(delNode.getRightNode()));
				System.out.println("value:"+value+"有两个子节点，已经删除！");
			}else {
				//3、待删除的节点不是叶子节点：它有一个子节点
				//如果删除的节点只有左子节点
				//如果要删除的结点有左子结点 
				if(delNode.getLeftNode() != null) {
					if(parent != null) {
						if(parent.getLeftNode().getData() == value) {
							parent.setLeftNode(delNode.getLeftNode());
						}else {
							parent.setRightNode(delNode.getLeftNode());
						}
					}else {
						rootNode = delNode.getLeftNode();
					}
					
				}else{
					if(parent != null) {
						if(parent.getLeftNode().getData() == value) {
							parent.setLeftNode(delNode.getRightNode());
						}else {
							parent.setRightNode(delNode.getRightNode());
						}
					}else {
						rootNode = delNode.getRightNode();
					}
				}
				System.out.println("value:"+value+"有一个子节点，已经删除！");
			}
			
			
				
			
			
			
			
			
			
			
			
		}
		
		
	}
	
}




//二叉排序树节点类
class Node{
	
	private int data;
	private Node leftNode;
	private Node rightNode;
	
	
	
	public Node(Integer data) {
		super();
		this.data = data;
	}
	public Integer getData() {
		return data;
	}
	public void setData(Integer data) {
		this.data = data;
	}
	public Node getLeftNode() {
		return leftNode;
	}
	public void setLeftNode(Node leftNode) {
		this.leftNode = leftNode;
	}
	public Node getRightNode() {
		return rightNode;
	}
	public void setRightNode(Node rightNode) {
		this.rightNode = rightNode;
	}
	@Override
	public String toString() {
		return "Node [data=" + data + "]";
	}
	
	
	//添加节点
	public void add(Node node) {
		if(node == null) {
			return;
		}
		if(node.getData() > this.getData()) {
			if(this.getRightNode() == null) {
				this.setRightNode(node);
			}else {
				this.getRightNode().add(node);
			}		
		}else {
			if(this.getLeftNode() == null) {
				this.setLeftNode(node);
			}else {
				this.getLeftNode().add(node);
			}
		}	
	}
	
	//中序遍历
	public void infixOrder() {
		if(this.getLeftNode() !=null) {
			this.getLeftNode().infixOrder();
		}
		System.out.println(this.getData());
		if(this.getRightNode() !=null) {
			this.getRightNode().infixOrder();
		}	
	}
	
	
	
	//删除节点
	//需要知道该节点和他的父节点
	//写两个方法
	//1、找到待删除的节点
	public Node getDelNode(int value) {
		if(value == this.getData()) {
			return this;
		}else {
			if(value > this.getData() && this.getRightNode() != null) {//右侧
				return this.getRightNode().getDelNode(value);
			}else if(value < this.getData() && this.getLeftNode() != null) {
				return this.getLeftNode().getDelNode(value);
			}else {
				return null;
			}
		}
		
	}
	
	//2、找到待删除的节点的父节点
	public Node getDelParNode(int value) {
		if((this.leftNode != null && this.getLeftNode().getData() == value)||
				(this.rightNode != null && this.getRightNode().getData() == value)) {
			return this;
		}else if(this.getData() > value && this.leftNode != null ) {
			return this.leftNode.getDelParNode(value);
		}else if(this.getData() <= value &&  this.rightNode != null) {
			return this.rightNode.getDelParNode(value);
		}else {
			return null;
		}
	}
	
	
	
	
}

原文链接：https://blog.csdn.net/wangjiaee/article/details/106147402

你可能也喜欢