故名思意,线性回归是一种
线性模型
,线性模型形式简单、易于建模。许多功能更为强大的
非线性模型
可在线性模型的基础上通过引入层级结构或者高维映射而得。本文先从不同的角度讨论的线性回归,最后到贝叶斯线性回归
本文主要是从数学推导方面进行总结,所以
绝
大
部
分
都
是
公式
。首先给定一个训练集
和样本的标签
线性回归试图学得一个线性模型:
能够根据给定的
以尽可能准确的输出预测值,上面的
是模型的参数
也许开始之前先应该说一些关于频率派和贝叶斯派的区别作为铺垫,简单的来说,频率学派的观点是,对于一个
概率模型
,
参数
是
固定的
、未知的常量——因为参数就在那里,我们只需要按某种方法去达到它,最后可以看作是一个优化问题
而贝叶斯学派的观点是,参数是未知的变量,它自身也是遵循某个概率分布的,我们只有它的先验分布,需要根据观察到的数据来进行调整
线性回归
首先从频率派的角度出发,为了寻找最优的参数,定义一个损失函数
通过最小化损失来得到最优参数。例如有下面一组的样本,我们希望拟合出一条能够很好的体现样本的趋势的直线
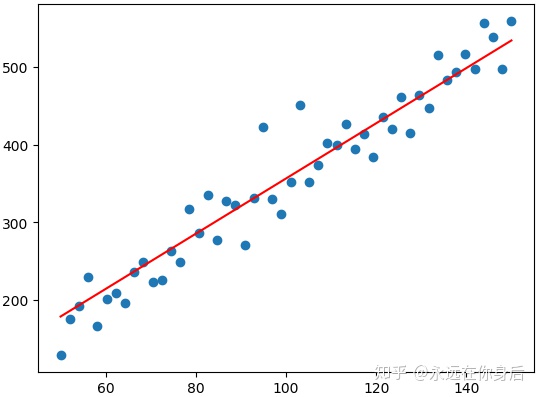
下面化简函数:
注意上式中红色部分的两项都是一个实数,且值相同,所以合为一项。接着,求最优参数:
对上式求导并令倒数为0:
得到:
接着,换一个角度来看线性回归。上面通过最小二乘法虽然拟合出了一条线能够较好的体现数据的内在规律,但是与绝大部分样本的真实值相比,还是有偏差的
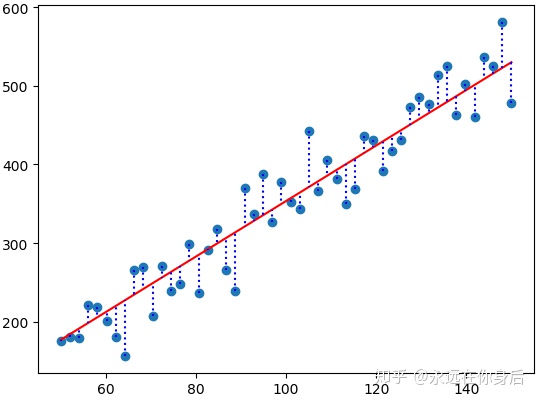
如上图所示,对于这种偏差,我们可以将它看作一个是一个噪声,一个服从高斯分布的
随机变量
,对于给定的
,它的真实值从下面的过程得到
其中
是噪声,
是给定的,
虽然是未知的,但是也是固定的,所以
是一个常量,因此
也可以看作是一个关于
随机变量
的函数
,
由此可以得到
的均值:
方差(噪声显然与
是独立的):
所以
。接着就可以通过
最大似然估计
来求解
,首先定义对数似然函数
求解最优值
可以看到,最后得到了和式(1)一样的结果,后面求导的过程都是一样的,就不展开了
岭回归
也就是代
正则化项的线性回归,在式(2)的基础之上,建立一个新的代价函数如下
上式中
是正则化系数,现在优化的目标就转为
函数了
对上面的函数求导并令导数为0,得到
从上式不难得到:
要更直观的理解
的作用,可以假设每个样本
只有一个属性
,
就是一个实数,所以:
可以看到,随着
的增大,
的值会渐渐减小,对
起到了抑制作用
同样,对于岭回归也可以换个花样——使用
最大后验估计
来推导,根据贝叶斯公式
其中
和
分别是似然和先验,并且:
接着,挨个来看这两项
以及
然后对
取对数,得到:
同样的套路,针对对数函数求解最优参数
将上式看作损失函数
然后对其求导
得到:
令
就得到了之前的结果
贝叶斯线性回归
以上,都是判别模型的线性回归,下面从贝叶斯学派出发,推导出贝叶斯线性回归。另外,这是一个
生成模型
同样,对于给定
,其
值从带噪声的函数中产生
其中
,
。这一点和前面是相同的,不同的是这里认为
自身也是有一个概率分布的,我们只知道它的一个先验分布:
可以通过观察到的数据来进行调整,得到后验分布。因此,先把前面从最大后验估计推导岭回归的公式拿过来
上面的红色部分前面式(3)(4)已经计算过了,就不赘述了。从上式可知,后验正比于先验与似然之积,且似然与先验都是高斯分布,所以
后验也是高斯分布
,并且设后验
,其中
是后验高斯的参数
至于为什么后验一定是高斯,可以参考这篇文章(如何理解「共轭分布」?)既然确定后验是服从高斯分布了,所以我们不必辛苦的计算整个公式了,只需要考虑
的
指数部分
就可以了
设指数部分为
,继续化简
到了这一步,可以通过高斯分布的性质,将它的参数求出来。首先,之前已经说过,后验
,按照公式把它的
指数部分给
写出来
然后,将它与我们的式子对比
由此不难得到后验高斯的参数,首先求出协方差并设其为矩阵
因为
是对称矩阵,所以可以得到均值
至此,得到了后验分布的参数,接着就能够根据给定的
进行预测了,设预测值为
因为
不再是存在一个固定的最优值,而是服从一个分布,也即是说它是一个随机变量,因此
也可以看作是一个随机变量的函数:
因此可以求导
的均值与方差(计算过程前面已经有相同的例子了)
因此
。以上是生成不带噪声的预测值,你也可以生成带噪声的预测值,设其为
因为
,所以
总之,不论生成的
还是
,它们服从于各自参数下高斯分布,如下图所示
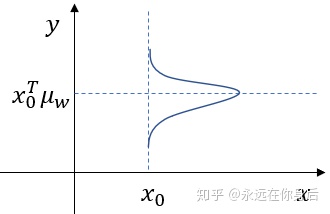
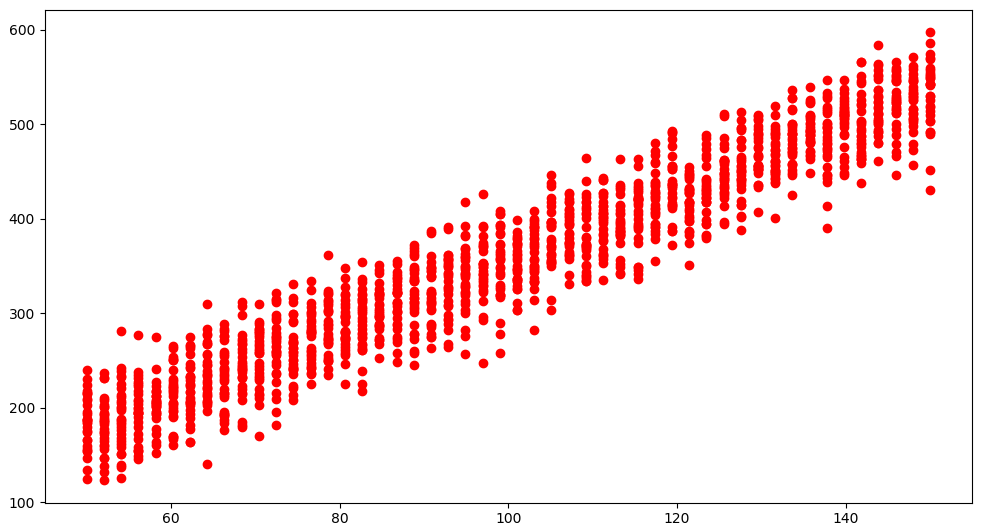
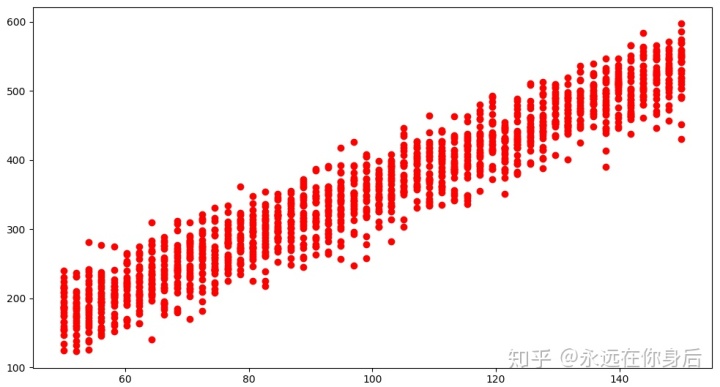
为了验证这一点,在一个区间内对
去不同的值,然后在每一个取值上对
进行多次预测,得到以下结果
总后,上代码:
import numpy as np
import matplotlib.pyplot as plt
def generate():
x = np.linspace(50, 150)
w = 3.6
y = w * x + np.random.normal(0, 30, size=x.size)
X = x.reshape(-1,1)
Y = y.reshape(-1,1)
return X, Y
class LinearRegression(object):
def __init__(self, w=None):
self.w = w
def least_square(self, X, Y):
'''
最小二乘法,通过给定样本学习参数
X: 样本矩阵,一行一样本
Y: 样本标签,Nx1矩阵
'''
inv = np.linalg.inv(np.dot(X.T, X))
self.w = inv.dot(np.dot(X.T, Y))
def ridge(self, X, Y, lam=3e-2):
# 岭回归
inv = np.linalg.inv(np.dot(X.T, X) + np.diag([lam]*X.shape[-1]))
self.w = inv.dot(np.dot(X.T, Y))
def predict(self, x):
'''
通过给定数据进行预测
'''
return np.dot(x, self.w)
class BayesRegression(object):
def __init__(self, sigma, mu=None, cov=None):
self.sigma = sigma # 噪声方差
self.mu = mu # 后验分布的均值
self.cov = cov # 后验分布的协方差矩阵
def fit(self, X, Y):
'''
拟合后验参数
'''
prior = np.eye(X.shape[-1]) # 先验协方差
A = np.dot(X.T, X) / self.sigma
self.cov = np.linalg.inv(A)
self.mu = self.cov.dot(np.dot(X.T, Y)) / self.sigma
def generate(self, x):
'''
根据给定数据,生成预测值
'''
mean = np.dot(x, self.mu).sum()
std = np.sqrt(np.dot(x, self.cov).dot(x)).sum()
return np.random.normal(mean, std, 1)
def generate_random(self, x):
'''
根据给定数据,生成带噪声的预测值
'''
mean = np.dot(x, self.mu).sum()
std = np.sqrt(np.dot(x, self.cov).dot(x) + self.sigma).sum()
return np.random.normal(mean, std, 1)
def main():
X, Y = generate()
lr = LinearRegression()
lr.ridge(X, Y)
x = np.array([50, 150]).reshape(-1,1)
y = lr.predict(x)
plt.figure()
plt.scatter(X, Y)
plt.plot(x, y, c='r')
for i, j in zip(X, Y):
plt.plot([i,i], [j, lr.predict(i)], c='b', linestyle='dotted')
plt.show()
if __name__ == "__main__":
# main()
X, Y = generate()
lr = LinearRegression()
lr.least_square(X, Y)
sigma = np.square(Y - np.dot(X, lr.w)).mean()
'''
关于贝叶斯线性回归需要将噪声的方差传给模型,但是计算方差又需要具体的w值
所以没办法只能通过判别模型的线性回归拟合w,然后再计算噪声的方差
'''
br = BayesRegression(sigma)
br.fit(X, Y)
xx = []
yy = []
count = 30
for x in np.linspace(50, 150):
xx += [x] * count
yy += [br.generate_random(x) for _ in range(count)]
plt.figure(figsize=(21,9))
plt.scatter(xx, yy, c='r')
plt.show()