博客

分别使用字符串和数组的方式，数组更简便一些

import java.util.Scanner;
public class test26 {
    //将字符串转化为数字
    public  static int function26(String s) {
        int flag = 0;//标志位用来判断字符串第一位是否为+和-
        int number = 0;//定义最后要返回的数
        int B = 1;//定义了每一位数字要乘以的倍数，个位乘1，十位乘10
        if (s.charAt(0) == '-') {
            flag = -1;//如果第一位是减号，则标志位变为-1
        }
        if (s.charAt(0) == '+') {
            flag = 1;//如果第一位是加号，则标志位为1，
        }//最后的数字乘以标志位
        //****************************************
        //由于第一位是符号比第一位不是符号要多考虑一位的遍历
        //第一位是符号，如果能把符号判断完成之后变为0，则不需要分情况讨论
        //但是charAt方法底层的value被final修饰，无法改变对应值，
        //因而一种方法是分情况讨论，另一种情况就是数组实现
        if (flag == 0) {//遍历
            for (int i = s.length()-1; i >=0; i--) {
                if (s.charAt(i) < '0' || s.charAt(i) > '9') {
                    return 0;
                } else {//要注意这里的关键，‘0’字符在表中有对应的数值，和‘1’字符差1
                    //因而相减就能够得到该位的数字值，这里倍数是从1开始，所以从后往前遍历
                    number = number + (s.charAt(i) - '0') * B;
                    B = B * 10;//每次遍历，倍数++
                }
            }
            return number ;
        } else {//有符号的情况
            for (int i = s.length()-1; i >0; i--) {
                if (s.charAt(i) < '0' || s.charAt(i) > '9') {
                    return 0;
                } else {
                    number = number + (s.charAt(i) - '0') * B;
                    B = B * 10;
                }
            }
        }
        return number * flag;//最后要返回的数要乘以一个flag符号数
    }
    public static void main(String[] args) {
        //将一个字符串转化为一串数字
        Scanner scanner=new Scanner(System.in);
        String s1=scanner.nextLine();
        int a=function26(s1);
        System.out.println(a);
    }
}

import java.util.Scanner;

public class test27 {
    public static int function27(String s){
        //使用数组的方法
        char[]arr= s.toCharArray();
        //设立标志位
        int flag=1;
        if (arr[0]=='+'){
            flag=1;
            arr[0]='0';
            //这里设置位0是为了遍历时不用刻意区分有无符号的情况
        }
        else if (arr[0]=='-') {
            flag = -1;
            arr[0] = '0';
        }
        int sum=0;//最后输出的值
        for (int i = 0; i < s.length(); i++) {
            if (arr[i]<'0'||arr[i]>'9'){
                sum=0;
                break;
            }
            sum=sum*10+arr[i]-'0';
        }
        return sum*flag;
    }

    public static void main(String[] args) {
        Scanner scanner=new Scanner(System.in);
        String s1=scanner.nextLine();
        int a=function27(s1);
        System.out.println(a);
    }
}

import java.util.Scanner;
public class test28 {
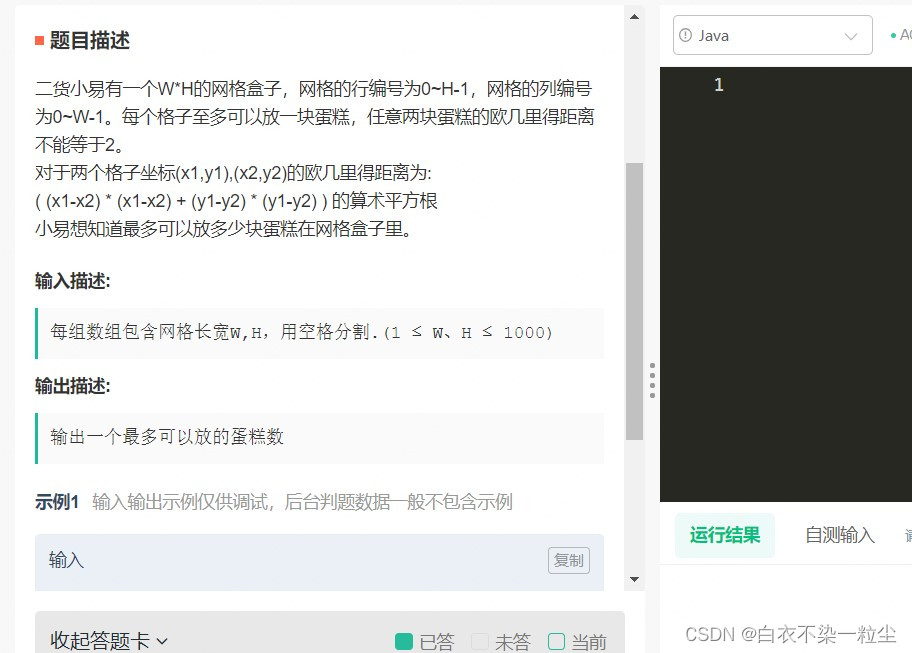
    //该题主要是去推导一个数学边界
    //同时使用二维数组进行一个有效判定
    //推导过程:1.由题可得算数平方根位为2，则
    //(x1-x2)*(x1-x2)+(y1-y2)*(y1-y2)=4
    //2.(x1-x2)*(x1-x2)看作A，(y1-y2)*(y1-y2)看作B，
    // 有下列五种情况可以满足
    //2+2 1+3 3+1 0+4 4+0  但前三种都没有解(x1,x2等都是整数)
    //3.于是只有第4和第五种情况可满足
    //x1-x2=2; y1=y2;或者y1-y2=2；x1=x2;
    //对应到题干中则是[i][j+2]   [i+2][j]时欧几里得距离为2

    public static void main(String[] args) {
        Scanner scanner=new Scanner(System.in);
        //w*H 分为为行和列即上述分析的i和j
        int W=scanner.nextInt();
        int H=scanner.nextInt();
        int count=0;
        int arr[][]=new int[W][H];
        for (int i = 0; i < W; i++) {
            for (int j = 0; j < H; j++) {
                if (arr[i][j]==0){
                    count++;
                    //初始值都为0，且第一个点定为第一个存蛋糕的位置
                }
                //j+2可能最后数组越界
                if (j+2<H) {
                    arr[i][j + 2] = 1;
                }
                if (i+2<W) {
                    arr[i + 2][j] = 1;
                }
            }
        }
        System.out.println(count);

    }
}