线性回归(Linear regression)是利用称为线性回归方程的最小二乘函数对一个或多个自变量和因变量之间关系进行建模的一种回归分析。这种函数是一个或多个称为回归系数的模型参数的线性组合。只有一个自变量的情况称为一元回归,大于一个自变量情况的叫做多元回归。。
多元线性回归模型的一般形式
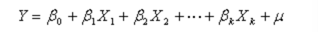
其中,Y为因变量,X为自变量,上式中共有k个自变量和一个常数项。如果自变量经过标准化处理,则上式没有常数项,换句话说,Y的期望值与自变量的函数关系如下:
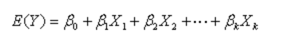
上式也被称为多元总体线性回归方程。
如果有n组观测数据,
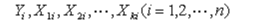
则可以采用方程组形式表示
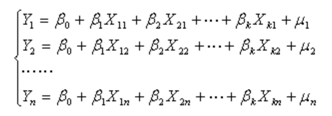
其矩阵形式为

简化形式为
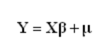
使用多元线性回归必须满足如下的几个条件:(1) 因变量Y和自变量X之间具有线性关系。(2) 各观测值Y相互独立。(3) 残差e服从均值为0,方差为δ^2的正态分布,也就是对自变量的任意一组观测值,因变量Y具有相同的方差,且服从正态分布。
本次数据集为machine.data,要求我们在给定硬件的其他相关属性的情况下预测计算机硬件的相对性能。
接下来我们开始编程吧
首先导入库
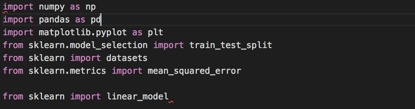
载入数据集

打印前几行看看是否载入成功了
结果如下

接下来就是选择特征,我们需要选择适合模型拟合的数值字段
怎么看字段是否适合呢?使用data.info就可以了
完整代码在2.py
结果如下

我们可以看到,除了前两个变量之外,其余的都是数字。 我们只选择数字字段。
所以使用下面的代码进行过滤

同样打印出来看看是否合适了
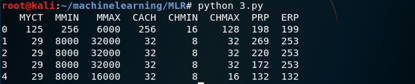
完整代码在3.py
结果如下
然后我们来选择预测值和目标变量

切割训练集,测试集

在我们进行拟合之前,让我们对数据进行标准化,使数据以均值为中心并具有单位标准差。
接下来该进行拟合了

下面代码中系数R ^ 2定义为(1-u / v),其中u是残差平方和((y_true-y_pred)** 2).sum()和v是平方和的总和((y_true – y_true.mean())** 2).sum()。

完整代码在4.py
打印出系数的预测值、均方误差、方差分

可以看到R^2和MSE的结果都很好。
MSE在前面的实验中有提到,这里解释下R^2
决定系数R^2,取值范围为[0,1],代表自变量能够解释因变量的比例,其值越接近1,说明模型对数据的拟合程度越好。
我在最开始使用了matplotlib库,现在就可以绘出通过预测得出的一条线,我们可视化拟合的好处。
完整代码在MLR.py
运行结果如下

这条线是由模型根据数据集训练后得出的,而蓝色的点是测试集,可以看到蓝色的点基本分布在线上或者左右,比较好地拟合了我们的训练结果。
参考:
1.《机器学习》(西瓜书)
2. https://zh.wikipedia.org/wiki/%E7%B7%9A%E6%80%A7%E5%9B%9E%E6%AD%B8
3. https://acadgild.com/blog/multiple-linear-regression
4. https://www.jianshu.com/p/2ce27e88d78c
5. https://blog.csdn.net/wx_blue_pig/article/details/79791906