博客

222.完全二叉树的节点个数

给你一棵 完全二叉树 的根节点 root ，求出该树的节点个数。

完全二叉树 的定义如下：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 1~ 2h 个节点。



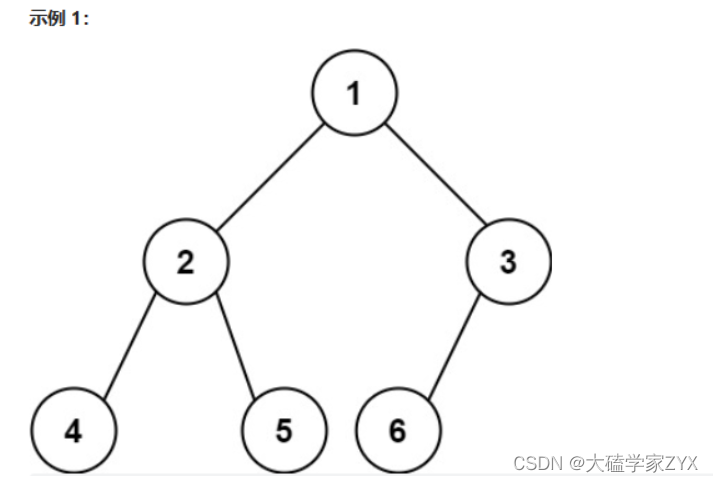
输入：root = [1,2,3,4,5,6]

输出：6


示例 2：


输入：root = []

输出：0

完全二叉树、完美二叉树和满二叉树

1. 
   完美二叉树
   
   （Perfect Binary Tree）：
   
   每一层都是完全填满的，即每一层的所有节点都存在，没有空缺
   
   。也就是说，如果树的高度为h，则有2^h – 1个节点。
2. 
   满二叉树
   
   （Full Binary Tree）：
   
   每个节点或者有2个子节点（左子节点和右子节点），或者没有子节点（叶子节点）
   
   。也就是说，没有只有一个子节点的节点。
3. 
   完全二叉树
   
   （Complete Binary Tree）：
   
   除了最底层外，其他各层的节点数都要达到最大，且最底层必须从左到右填入
   
   。也就是说，如果在某一层有空缺，那么该空缺必须在该层的最右侧。

（注意满二叉树和完美二叉树并不是一个概念）

普通二叉树的写法

思路

求节点的数量和

求高度

类似，递归写法依旧是用后序遍历，统计左右子树的节点数量并返回上一层，进行累加。

完整版

• 每个节点都遍历了一遍，时间复杂度是O(N)

class Solution {
public:
    int countNodes(TreeNode* root) {
     //终止条件
    if(root==NULL){
        return 0;
    }
    
    //后序遍历
    int leftNum = countNodes(root->left);
    int rightNum = countNodes(root->right);
    int Num = 1+leftNum+rightNum;
    
    return Num;


    }
};

完全二叉树的写法

思路

完全二叉树是

除了底层节点之外全满，并且底层节点从左到右没有断开

的二叉树。

当我们

计算满二叉树的时候，节点数量可以直接用公式

，假设满二叉树层数为n，那么节点数量就是

2^n-1

。例如下图中中间的完全二叉树，前三层的节点数量就是

2^3-1=7

。



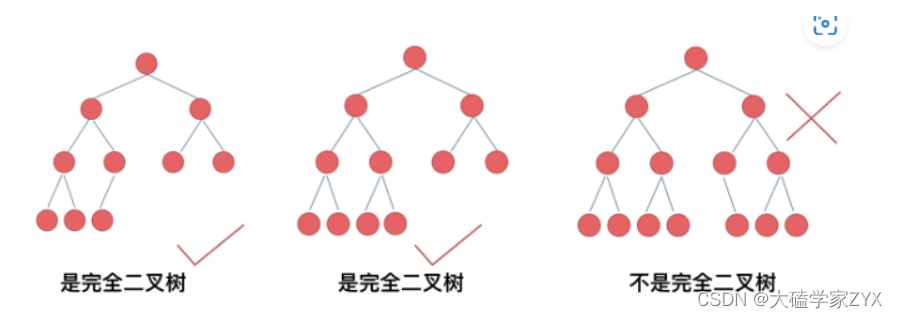
因此可以通过完全二叉树除了底层都是满的这一特性来计算节点数。

遍历一个二叉树的子树，其子树如果是满二叉树，可以先得到子树的深度，然后直接2^n-1。

下面问题就是如何判断子树是否是满二叉树，并计算其深度。

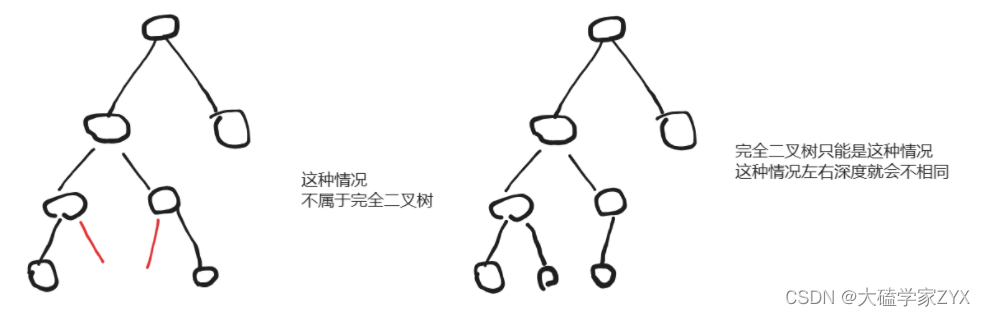
如果是满二叉树，向左遍历的深度和向右遍历的深度一定是相等的

，并且，

本题目规定了是一个完全二叉树，因此不存在左右深度相同但是中间存在NULL的情况

。如下图所示。



但是图中的完全二叉树，其左子树是满二叉树，因此可以计算。右子树继续向下遍历，遇到了单个节点，

单个节点也可以算满二叉树

，因此也可以计算满二叉树节点数量并返回上层。也就是说，

一直向下递归，一定可以遇到符合满二叉树条件的节点

，不会进入死循环，因为

最后的叶子节点一定是满二叉树

。



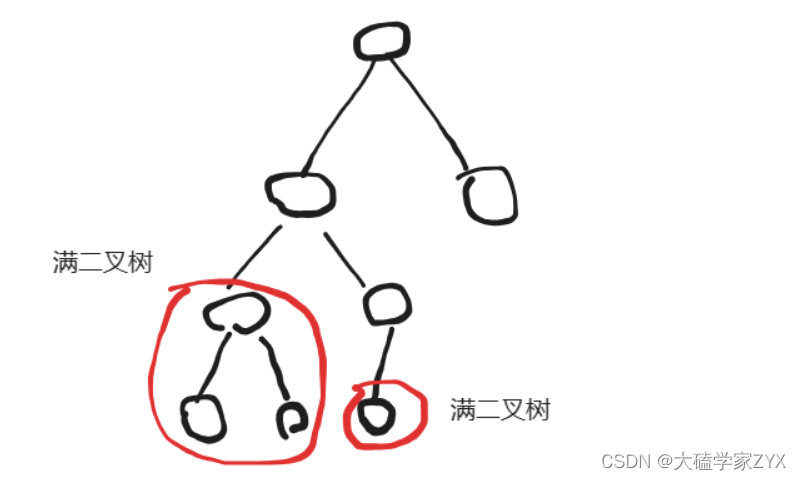
因此，我们可以先往左递归，计算左侧深度，再一直往右递归，计算右侧深度，如果两侧深度相同，说明子树是满二叉树，直接通过

2^n-1

计算其节点数目，返回给上一层。

这种写法的好处是，只需要遍历外侧节点，不需要遍历内侧，

在二叉树足够大的情况下，中间侧的节点都不遍历，只遍历左右侧节点，能节省较多的时间开销

。

伪代码

• 终止条件的计算里并没有用递归，终止条件里计算深度，单层逻辑依然是后序遍历的递归逻辑，和104.求二叉树最大深度的前序遍历写法并不一样

int getNum(TreeNode* root){
    
    //这种解法终止条件比较复杂，除了遇到空的情况，还要判断遇到满二叉树的情况
    //遇到空
    if(root==NULL){
        return 0;
    }
    //遇到满二叉树，返回公式计算的子树节点数，也是终止条件
    TreeNode* left = root->left;
    TreeNode* right = root->right;
    int leftDepth = 0;
    int rightDepth = 0;
    
    //一直向左计算深度
    //这里注意，当left=left->left==NULL的时候，leftDepth就不会++了，也就是说leftDepth统计的就是真实的深度
    while(left){
        left = left->left;
        leftDepth++;   
    }
    //一直向右计算深度
 
    while(right){
        right = right->right;
        rightDepth++;
    }
    if(leftDepth==rightDepth){
        //指数计算方法：位运算
        // 此处注意(2<<1) 相当于2^2，所以leftDepth初始为0
        return (2<<leftDepth)-1;
    }
    
    //单层递归：后序遍历
    int leftNum = getNum(root->left);
    int rightNum = getNum(root->right);
    int Num = 1+leftNum+righNum;
    return Num;
    
    
    
}

位运算注意

c++中，2<<1相当于2的2次方，也就是说2<<1 = 4。

2<<0是2的1次方，相当于没有移动

。因此

leftDepth

是从0开始的。但是计算的时候，相当于从2<<0也就是2的1次方开始计算。

leftDepth初值必须取0的原因

在最后计算节点数量的时候，根节点那一层的数量应该是

2<<0-1

，所以

深度的初值必须从0开始取

。

二叉树深度/高度初始值的问题

对于二叉树的深度或高度的定义，有两种常见的约定：

1. 一种是将根节点的深度（或高度）视为0，那么只有一个节点的树的深度（或高度）为0，两个节点的树的深度（或高度）为1，以此类推。
2. 另一种是将只有一个节点的树（只有根节点）的深度（或高度）视为1，那么两个节点的树的深度（或高度）为2，以此类推。

这两种约定都是常见的，选择哪一种主要取决于具体的应用场景和需求。例如，在

111.二叉树最小深度

题目中，显然采用了第二种约定，

将只有一个节点的树（只有根节点）的深度视为1。在这种约定下，计算最小深度时，对于每个节点，我们都需要计算其左右子树的最小深度，然后加1（因为需要算上该节点自身）

。

但是在本题

222.完全二叉树的节点个数

中，

当计算满二叉树的节点数量时，采用了将根节点深度视为0的约定

，因为根据公式，满二叉树的节点数为

2^d - 1

，其中d是树的深度，

根节点深度为0，满二叉树节点数量就为

2<<0 - 1 = 2 - 1 = 1

，这与实际情况（只有一个节点）相符

。这也是一个合理的约定，因为在这种情况下，我们关心的是整个树的结构，而不是单个节点的深度。

总的来说，对于树的深度（或高度）的定义没有固定的规定，取决于具体的应用场景和需求。只要在实际应用中保持一致，就不会出现问题。

什么时候使用位运算

在C++中，如果想计算

a

的

b

次方，通常使用

<cmath>

库中的

pow(a, b)

函数。

但是，如果

b

是2的幂，也就是说

我们要计算的是2的多少次方

，

使用位运算会更快

，因为位运算通常比浮点数运算更快。这是为什么本题中使用了位运算。然而，

如果

b

不是2的幂，那么位运算就不能用来计算

a

的

b

次方了

。

正常情况下，不是2的多少次方的运算，都是通过库的

pow(a,b)

来解决。示例：

#include <iostream>
#include <cmath> // 引入cmath库以使用pow函数

int main() {
    double a = 2.0;
    double b = 3.0;
    double result = std::pow(a, b); // 计算a的b次方
    std::cout << "The result of " << a << " to the power of " << b << " is: " << result << std::endl;
    return 0;
}


pow(a, b)

函数对于所有的浮点数

a

和

b

都有定义，这意味着它可以用来计算诸如

pow(2.0, 0.5)

（即2的平方根）这样的表达式。但如果你只需要计算整数的整数次幂，也可以使用标准库

<cmath>

中的

pow

函数，如

std::pow(2, 3)

。

但要注意的是，使用浮点数的运算可能会存在一定的精度问题，尤其是在处理大数或者需要高精度计算的情况下，这点在实际编程中需要特别注意。

完整版

class Solution {
public:
    int countNodes(TreeNode* root) {
       //使用完全二叉树的特性完成题目
        
        //终止条件
        if(root==NULL){
            return 0;
        }
        TreeNode* left = root->left;
        TreeNode* right = root->right;
        int leftDepth = 0;
        int rightDepth = 0;
        while(left){
            left = left->left;
            leftDepth++;
        }
        while(right){
            right = right->right;
            rightDepth++;
        }
        if(leftDepth==rightDepth){
            return (2<<leftDepth)-1;
        }
        
        //单层递归：后序遍历
        int leftNum = countNodes(root->left);
        int rightNum = countNodes(root->right);
        int Num = 1+leftNum+rightNum;
        return Num;

    }
};

时间复杂度

这种做法的时间复杂度是

O(logn×logn)

。原因是它结合了二分查找和递归的思想。

在每一层递归中，代码首先通过两个while循环

计算左子树和右子树的深度（高度）

，这个操作的

时间复杂度是O(log n)

，因为

在完全二叉树中，树的深度（高度）是log n

（这里的n是树的节点总数）。

然后，如果左子树和右子树的深度（高度）相同，说明左子树是一棵满二叉树，直接通过公式

(2<<leftDepth)-1

计算节点数。如果左子树和右子树的深度（高度）不同，代码会递归地在左子树和右子树中调用

countNodes

函数。

注意，由于

每一层递归中，代码都在二叉树中的一半节点中进行查找

，这与二分查找的思想类似。所以，这个代码的总时间复杂度是O(log n × log n)。

为什么是O(log n × log n)而不是O(log n)呢？这是因为

在每一层递归（深度）中，代码都要进行O(log n)的操作（两个while循环计算深度）

，并且

树的深度也是O(log n)

，所以总的时间复杂度就是O(log n × log n)。

与后序遍历递归O(N)的对比

对于完全二叉树，O(log n × log n)的时间复杂度通常优于O(N)。

首先注意：O(log n × log n)=O((log n)^2)，

虽然是平方级别的复杂度，但仍然是对数级别的复杂度。对数级别的复杂度在大多数情况下优于线性复杂度

。O(log n × log n)通常被用来描述那些每一层复杂度为O(log n)，并且总共有log n层的算法。这样描述有助于理解算法的工作机制，但是实质上O(log n) × O(log n) = O((log n)^2)。

在第二种做法中，代码利用了完全二叉树的特性，

只需要在一半的节点上进行操作。并且，每一层递归都会将问题规模减半，因此它的时间复杂度是对数级别的

。

相比之下，第一种做法中的后序遍历算法需要访问树中的每一个节点一次，因此

它的时间复杂度是线性的

。

但需要注意的是，这只是理论上的比较。在实际情况中，由于各种因素（例如计算机的缓存效果、函数调用的开销等），实际性能可能会有所不同。实际上，如果树的大小不是特别大，那么简单的后序遍历算法可能会更快一些，因为它的实现更简单，没有额外的函数调用开销。

在理论上，O(log n × log n)的时间复杂度优于O(N)，但在实际应用中，哪一种算法更好可能取决于具体的情境。