一.损失函数
问题引入:如何给数据集选择一个正确的权重W以及怎么用训练数据来得到W的最优值。
有一些训练数据集x和y,通常又N个样本,其中x是算法的输入,在图片分类问题里,x其实是图片每个像素点所构成的数据集,y是希望预测出来的东西,通常称之为标签或目标。我们把最终的损失函数定义为

二.多分类SVM损失函数

问题:这个公式到底是在计算什么?
这个损失是在说如果真实分类的分数比其他分数高很多,这是正确的情况,那要高出多少呢?高出一个安全的边距;如果真实分类的分数不能够比其他分类高出那么多,那就会得到损失,这是不好的情况。
S是通过分类器预测出来的不同类的分数,而
y
i
y_i
y
i
这个整数表示这个样本正确的分类标签,所以
S
y
i
S y_i
S
y
i
表示训练集的第i个样本的真实分类的分数。这种损失函数也可以说成是一个合页损失函数,画出的图像如下:

这里的x轴表示,是训练样本的真实分类的分数;y轴则表示损失;可以看到随着真实分类的分数的提升,损失会线性下降,一直到分数超过了一个阈值,损失函数就变成0,此时已经成功的对这个样本进行了分类。

接下来对刚才例子中的三个样本进行损失的计算:
(1)对第一个训练样本进行多分类SVM损失函数的计算,得到损失值2.95

这也从一定程度上表明这个损失值2.9是分类器对这个个训练样例训练的多好的一个量化衡量指标。
(2)对第二个训练样本进行多分类SVM损失函数的计算,得到损失值0

3)对第三个训练样本进行多分类SVM损失函数的计算,得到损失值12.9

问题:为什么要选择加上1这个数?
答: 其实在一定程度上是一个任意的选择,这实际上就是一个出现在损失函数中的常数,我们并不真正关心损失函数中分数的绝对值,关心的只是这些分数的相对差值,需要的是正确的分数远远大于不正确的分数,所以实际上如果把整个W参数放大或缩小,那么所有的分数都会放大或缩小。
算出了3个样本的损失值之后,最终对于整个训练数据集的损失函数是这些不同案例的损失函数的平均值:

这一定程度上就是我们的量化衡量,5.27反应了我们的分类器在数据集上有多不好。
问题:损失函数的可能的最大最小值是多少?
答:最小值是0,可以想象所有的分类,如果它们的正确分数都非常大,那么得到的所有分类的损失函数为0,那么总的损失函数也就为0;最大值是无穷大,可以从合页损失函数这个图像看出,正确分数越低,损失函数结果也就趋向于无穷大。
问题:当初始化这些参数并且从头开始训练,通常先用一些很小的随机值来初始化W,分数的结果在训练初期倾向于呈现较小的均匀分布的值,如果所有的分数近乎为0,并且差不多相等,那么使用SVM时的损失函数预计如何?
答:分数的数量减去1。因为如果对所有不正确的类别遍历了一遍,那么实际上遍历了C-1个类别,这些类别中的每一个,这两个分数差不多相同,那么就会得到一个值为1的损失项,所以将会得到C-1。
问题:如果将对于SVM的所有错误分数求和会发生什么?将所有正确分数求和会发生什么?将所有的都求和呢?
答:损失函数增加1。同时在实际应用中这么做的原因在于通常损失函数为0的时候说明算法很好,所以没有损失什么。
问题:如果使用平均值而不是求和呢?
答:损失函数不会改变。分类的数量需要提前确定,当选择数据集的时候,因为这只是将整个损失函数缩小了一个倍数,所以并没有什么影响。
问题:如果改变损失函数的公式,在max上加上一个平方项,,这会成为另一个不同的分类算法吗?
答:会变成不同的分类算法。这里的想法在于我们用一种非线性的方法改变了在好和坏之间的权衡,所以实际上计算了另一种损失函数。
下面是一些向量化的代码片段:

假设有这样的数据集:
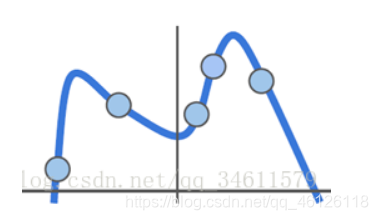
这里为训练数据拟合了一些曲线,如果告诉分类器做的唯一的事情是尝试拟合训练数据,它可能会具有非常曲折的曲线,尝试完美的分类所有的训练数据点,但我们实际关心的是测试数据的性能,事实上,期望的分类器可能预测的是下图中绿色的直线,而并不是完美的拟合训练数据。
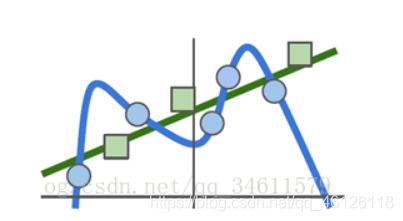
这在机器学习领域是一个非常核心的基础性问题,通常的解决方式是正则化,所以在这里要为损失函数添加一个附加的正则化项:

一般的是让模型以这种方式选择更简单的W;这样一来,标准的损失函数就有了两个项:数据丢失项和正则化项。
实际上,有很多不同的类型正在实践中使用正则化的方法,常见的有:

L1用于 取稀疏矩阵,L2用于均衡所有权重值,目的都是为了防止过拟合
问题:L2正则化如何度量复杂性的模型?
通过以下的具体例子来阐述:假设有一些训练样本x,有两个不同的W供选择,当进行线性分类时,真正讨论的是x与W的点乘结果,而两种乘积的结果是相同的,那么哪种情形下的L2回归性会好一些呢?

W2的L2回归性好一些,它具有比较小的范数,所以L2回归可以用一种相对粗糙的方式去度量分类器的复杂性,L2正则化的作用是它更能够传递x中不同元素值的影响,它的鲁棒性可能更好一点;L1正则化是相反的,使用L1正则化则更倾向于选择W1(倾向于让大部分元素接近0);所以问题是如何度量复杂度,它视不同问题而定,针对特殊的模型和数据及不同的设置,思考复杂度该如何度量;L1度量复杂度的方式可能是非零元素的个数,而L2更多考虑的是W整体分布,所以它具有更小的复杂性。
三.多项逻辑回归损失函数(Softmax)
针对SVM分类器,只是想要正确分类的分数比不正确类别的得分要高才好,并没有对这些得分做过多的解释;但对于多项逻辑回归损失函数,将赋予这些分数一些额外的含义,并且利用这些分数针对类别去计算概率分布。
现在我们要做的是促使计算得到的概率分布,就是通过Softmax计算的结果去匹配目标概率分布,即正确的类别应该具有几乎所有的概率(

损失函数就是:

(真实类别的概率对数再取负值),用Softmax对分数进行转化处理并得到正确类别的损失函数是:

回到猫咪的例子中,这里并不是直接把分数放在损失函数里,而是将它们进行指数化处理,然后对他们进行归一化以保证它们的和是1,接着求出损失函数的结果。

这就是Softmax损失函数,也被称为多项式回归逻辑损失函数。
问题:Softamx损失函数的最大值和最小值是多少?
答:最小值是0,最大值是无穷大。希望针对正确的类别概率是1而不正确的概率是0,如果是这样,那么log函数里的自变量就会是1,即真实类别所对应的概率,损失函数值就为0;同样,当log函数里的值是0时,损失函数值就趋向于无穷大,但基本不会出现这样的情况。
问题:如果所有的分数都很小,近乎为0,那么损失值是多少?
答:损失值是logC。这是一个很好的纠错机制,如果用这个softmax损失来训练一个模型,应该在第一次迭代中检查,不是logC的话就是出了问题
四.Svm损失函数与Softmax损失函数的对比
对于svm是深入研究观察正确分类分值和不正确分类分分值的边距,而对于softmax是打算去计算一个概率分布,然后查看负对数概率正确的分类:
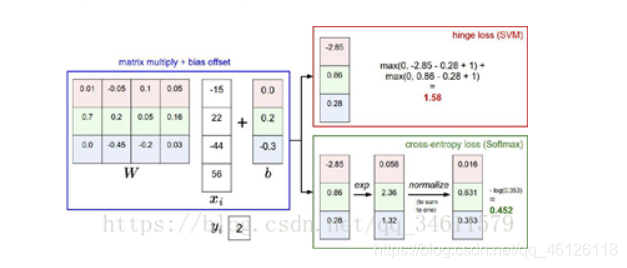
svm会得到这个数据点超过阈值要正确分类,然后不再关心这个数据点,而softmax总是试图不断提高每一个数据点都会越来越好。
回顾一下整个过程:

上述图中的内容是一个通用的概述,那么如何才能真正发现一个W使损失最小化,这就是优化的问题了。
五.优化
1)在实践中,倾向于从某个解决方案开始,使用多种不同的迭代方法,然后逐步对它进行改进,一种方法就是随机搜索:需要有很多的权重值随机采样,然后将它们输入损失函数,看看效果如何,但这不是一个好的方法。
(2)另一种方法是梯度下降:梯度是偏导数的向量,它指向函数增加最快的方向,相应的负梯度方向就指向了函数下降最快的方向;梯度给出了函数当前点的一阶线性逼近,很多深度学习应用都是在计算函数的梯度,然后利用这些梯度迭代更新参数向量。
使用有限差分的方法计算梯度,如下图中的过程:

可以想象如果这里的卷积神经网络非常大,那么计算函数f会很慢,所以在实际应用中,并不会使用有限差分的计算方法,相应的使用微积分的方法只需要写出损失函数的表达式就能很快计算出梯度。
总结:
(1)使用数值梯度的方法:近似值、速度慢、容易写;
(2)使用分析梯度的方法:精确值、速度快、容易出错。
六.图像特征
线性分类器是将原始像素取出,将这些原始像素直接传入线性分类器,但是实际操作中,直接输入原始像素值传递给线性分类器的表现不是很好;所以,当使用神经网络大规模运用之前常用的方式是两步走策略:首先,计算图片的各种特征代表,例如计算与图片形象有关的数值;接着,将不同的特征向量合到一块,得到图像的特征表述;然后将图像的特征表述作为输入源传入到线性分类器。
对于不能用一个决策边界划分的数据集,如果采用一个灵活的特征转换,得到它的转换特征,就可以把复杂的数据集变成线性可分,就可以用线性分类器正确分类。

下面介绍几个特征表示的例子:
(1)一个特征表示非常简单的例子就是颜色直方图:

获取每个像素值对应的光谱,把它分到柱状内,将每个像素都映射到这些柱状里,然后计算出每个不同柱状中像素点出现的频次,就可以知道图像的颜色状况。
(2)另一个例子:在神经网络兴起之前,一个常用的特征向量就是方向梯度直方图,由Hubel和Wiesel发现的人类视觉系统中,边缘非常重要;而特征表示的有向梯度直方图就是尝试这样的方法,测量图像中边缘的局部方向,如下图所示:

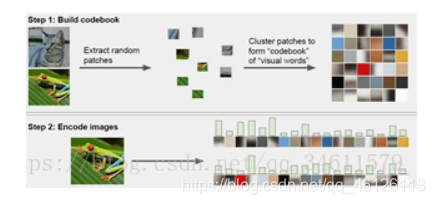
(3)还有一个特征表示的例子就是词袋;这是从自然语言处理中获得的灵感,用一个特征向量表示一段话的方式是计算不同词在这段胡中出现的次数;将这种方式应用于图像,将图像转换为一段话并不容易,所以要定义一个视觉单词字典。
方法:首先获得一堆图像,从这些图像中进行小的随机快的采样,然后用K均值等方法将它们聚合成簇,得到不同的簇中心,这些簇中心可能代表了图像中视觉单词的不同类型;接着就可以利用这些视觉单词给图像进行编码,记录它们出现在图像中的次数。